Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104905 by mohammad17 last updated on 24/Jul/20

Answered by OlafThorendsen last updated on 24/Jul/20

x^4 +x^3 +x^2 +x+1 = 0 ((1−x^5 )/(1−x)) = 0 x^5 = 1 x = e^((2ikπ)/5) , k∈{1,2,3,4}

$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}−{x}^{\mathrm{5}} }{\mathrm{1}−{x}}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{5}} \:=\:\mathrm{1} \\ $$$${x}\:=\:{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{5}}} ,\:{k}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$

Answered by ajfour last updated on 24/Jul/20

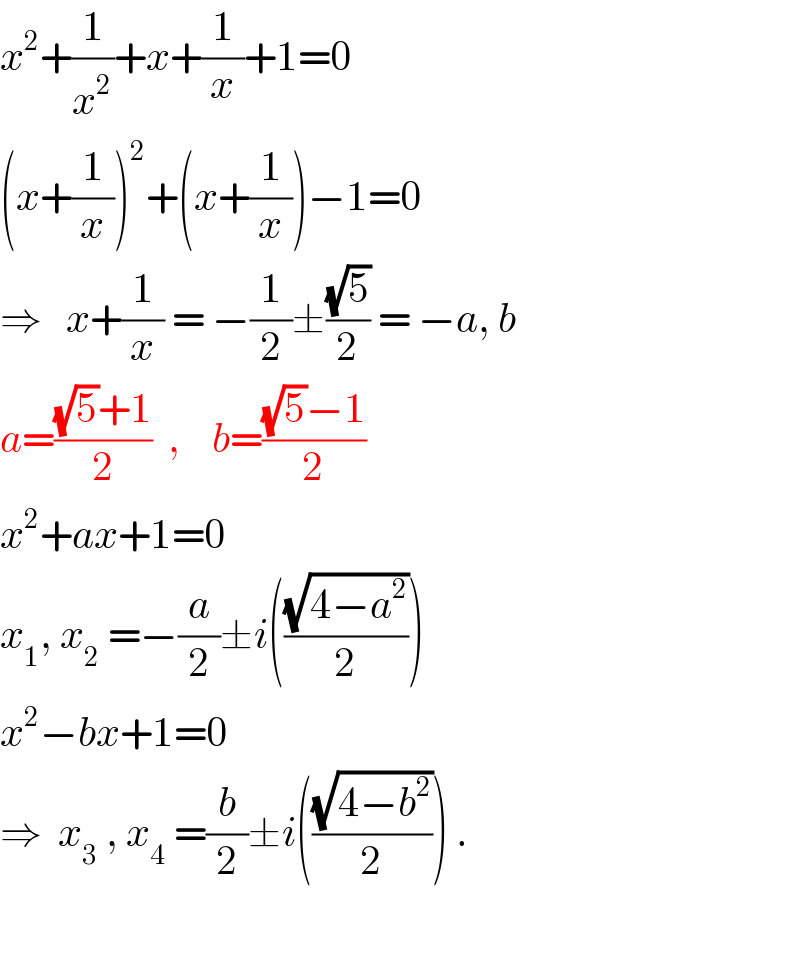
x^2 +(1/x^2 )+x+(1/x)+1=0 (x+(1/x))^2 +(x+(1/x))−1=0 ⇒ x+(1/x) = −(1/2)±((√5)/2) = −a, b a=(((√5)+1)/2) , b=(((√5)−1)/2) x^2 +ax+1=0 x_1 , x_2 =−(a/2)±i(((√(4−a^2 ))/2)) x^2 −bx+1=0 ⇒ x_3 , x_4 =(b/2)±i(((√(4−b^2 ))/2)) .

$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}=\mathrm{0}\: \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}+\frac{\mathrm{1}}{{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:−{a},\:{b} \\ $$$${a}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\:\:,\:\:\:\:{b}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{ax}+\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} \:=−\frac{{a}}{\mathrm{2}}\pm{i}\left(\frac{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$$${x}^{\mathrm{2}} −{bx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}_{\mathrm{3}} \:,\:{x}_{\mathrm{4}} \:=\frac{{b}}{\mathrm{2}}\pm{i}\left(\frac{\sqrt{\mathrm{4}−{b}^{\mathrm{2}} }}{\mathrm{2}}\right)\:. \\ $$$$ \\ $$

Answered by 1549442205PVT last updated on 25/Jul/20

⇔x^2 (x^2 +x+(1/4))+((3x^2 )/4)+x+1=0 ⇔x^2 (x+(1/2))^2 +(x^2 /2)+((x/2)+1)^2 =0 This equation has no real solutions because LHS is sum of the non−negative terms and they isn′t equal to zero simultaneously

$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\left(\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{because}\:\mathrm{LHS}\:\mathrm{is}\:\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{non}−\mathrm{negative}\:\mathrm{terms}\:\mathrm{and}\:\mathrm{they}\:\mathrm{isn}'\mathrm{t} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{zero}\:\mathrm{simultaneously} \\ $$

Commented by 1549442205PVT last updated on 25/Jul/20

but that steps isn′t key .

$$\mathrm{but}\:\:\mathrm{that}\:\mathrm{steps}\:\mathrm{isn}'\mathrm{t}\:\mathrm{key}\:. \\ $$

Commented by Rasheed.Sindhi last updated on 25/Jul/20

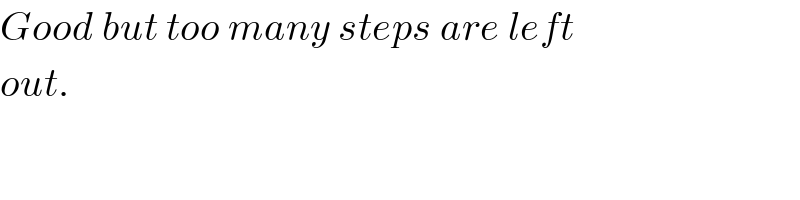
Good but too many steps are left out.

$${Good}\:{but}\:{too}\:{many}\:{steps}\:{are}\:{left} \\ $$$${out}. \\ $$

Commented by Rasheed.Sindhi last updated on 25/Jul/20

Yet an important step. If you were tronsforming from x^2 (x^2 +x+(1/4))+((3x^2 )/4)+x+1=0 to x^4 +x^3 +x^2 +x+1 no step were necessary. But if you do oppositely I think some steps are necessary to insert.

$${Yet}\:{an}\:{important}\:{step}. \\ $$$${If}\:{you}\:\mathrm{we}{re}\:{tronsforming}\:{from} \\ $$$$\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{x}+\mathrm{1}=\mathrm{0}\:{to} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\:{no}\:{step}\:{were} \\ $$$${necessary}. \\ $$$${But}\:{if}\:{you}\:{do}\:{oppositely}\:{I}\:{think} \\ $$$${some}\:{steps}\:{are}\:{necessary}\:{to}\:{insert}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com