
Question Number 104928 by bobhans last updated on 24/Jul/20
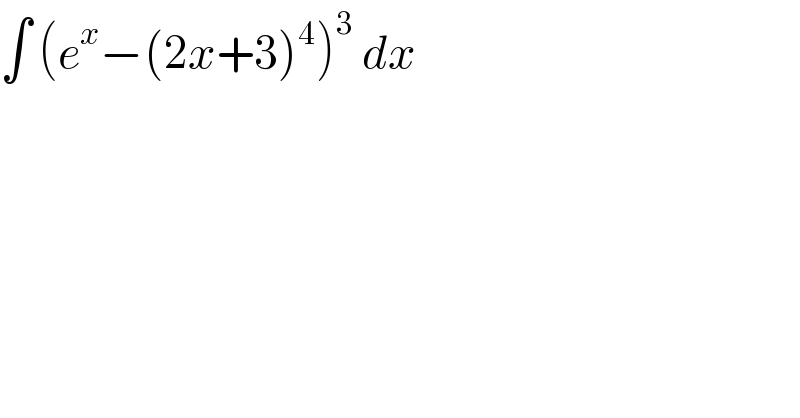
$$\int\:\left({e}^{{x}} −\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} \right)^{\mathrm{3}} \:{dx} \\ $$
Commented by kaivan.ahmadi last updated on 24/Jul/20
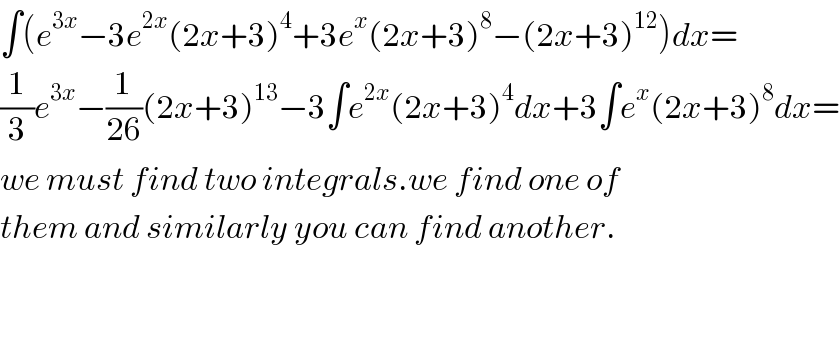
$$\int\left({e}^{\mathrm{3}{x}} −\mathrm{3}{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} +\mathrm{3}{e}^{{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{8}} −\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{12}} \right){dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} −\frac{\mathrm{1}}{\mathrm{26}}\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{13}} −\mathrm{3}\int{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} {dx}+\mathrm{3}\int{e}^{{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{8}} {dx}= \\ $$$${we}\:{must}\:{find}\:{two}\:{integrals}.{we}\:{find}\:{one}\:{of} \\ $$$${them}\:{and}\:{similarly}\:{you}\:{can}\:{find}\:{another}. \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 24/Jul/20

Commented by kaivan.ahmadi last updated on 24/Jul/20
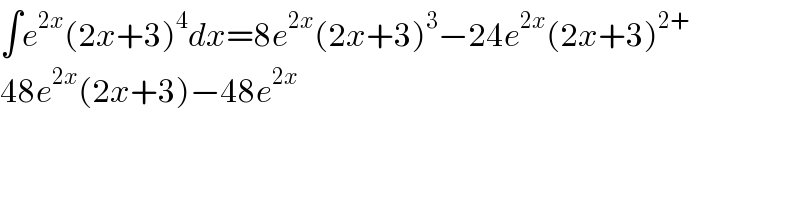
$$\int{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} {dx}=\mathrm{8}{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{3}} −\mathrm{24}{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}+} \\ $$$$\mathrm{48}{e}^{\mathrm{2}{x}} \left(\mathrm{2}{x}+\mathrm{3}\right)−\mathrm{48}{e}^{\mathrm{2}{x}} \\ $$
Commented by malwaan last updated on 25/Jul/20
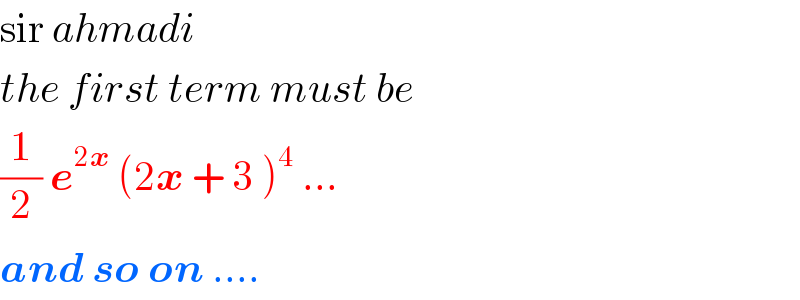
$$\mathrm{sir}\:{ahmadi} \\ $$$${the}\:{first}\:{term}\:{must}\:{be} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} \:\left(\mathrm{2}\boldsymbol{{x}}\:+\:\mathrm{3}\:\right)^{\mathrm{4}} \:... \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{so}}\:\boldsymbol{{on}}\:.... \\ $$
Commented by malwaan last updated on 25/Jul/20
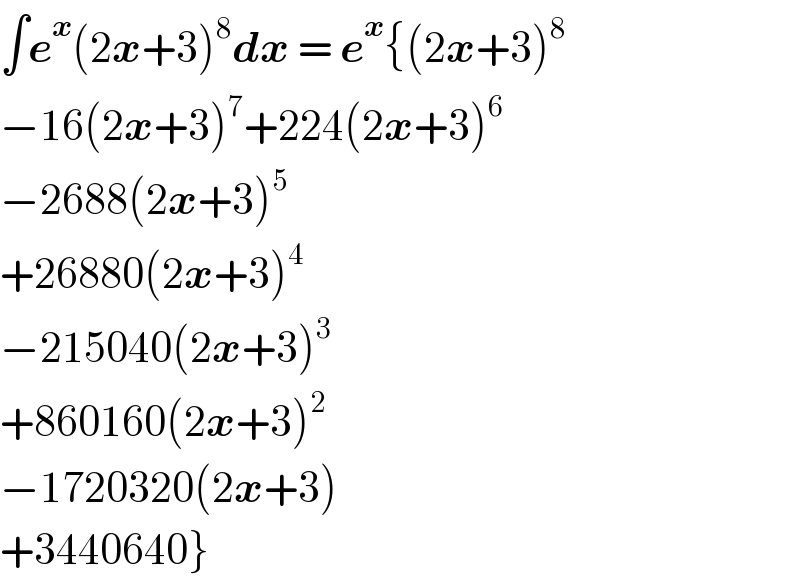
$$\int\boldsymbol{{e}}^{\boldsymbol{{x}}} \left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{8}} \boldsymbol{{dx}}\:=\:\boldsymbol{{e}}^{\boldsymbol{{x}}} \left\{\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{8}} \right. \\ $$$$−\mathrm{16}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{7}} +\mathrm{224}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{6}} \\ $$$$−\mathrm{2688}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{5}} \\ $$$$+\mathrm{26880}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{4}} \\ $$$$−\mathrm{215040}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{3}} \\ $$$$+\mathrm{860160}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$−\mathrm{1720320}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right) \\ $$$$\left.+\mathrm{3440640}\right\} \\ $$
