Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10493 by ABD last updated on 14/Feb/17

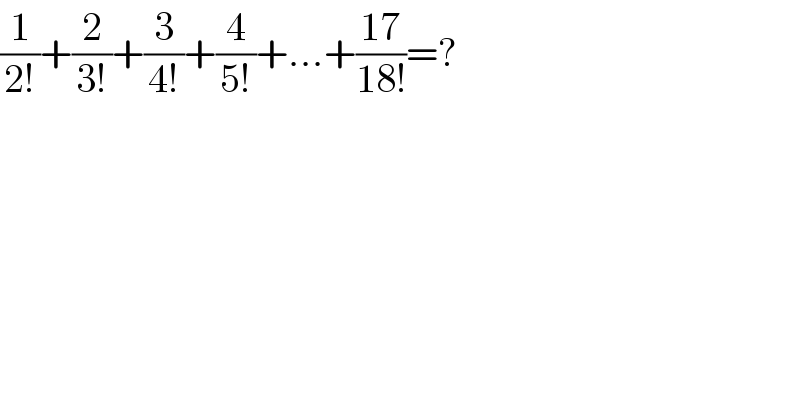
(1/(2!))+(2/(3!))+(3/(4!))+(4/(5!))+...+((17)/(18!))=?

$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+\frac{\mathrm{4}}{\mathrm{5}!}+...+\frac{\mathrm{17}}{\mathrm{18}!}=? \\ $$

Answered by mrW1 last updated on 14/Feb/17

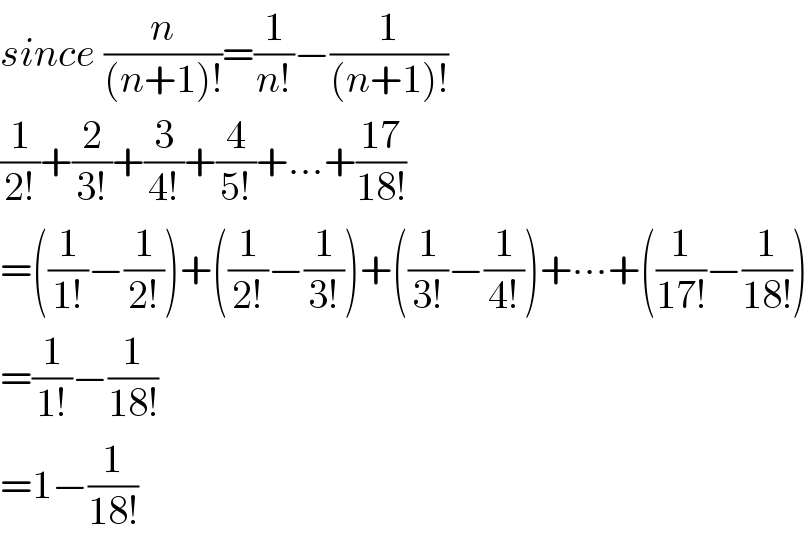
since (n/((n+1)!))=(1/(n!))−(1/((n+1)!)) (1/(2!))+(2/(3!))+(3/(4!))+(4/(5!))+...+((17)/(18!)) =((1/(1!))−(1/(2!)))+((1/(2!))−(1/(3!)))+((1/(3!))−(1/(4!)))+∙∙∙+((1/(17!))−(1/(18!))) =(1/(1!))−(1/(18!)) =1−(1/(18!))

$${since}\:\frac{{n}}{\left({n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+\frac{\mathrm{4}}{\mathrm{5}!}+...+\frac{\mathrm{17}}{\mathrm{18}!} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}\right)+\centerdot\centerdot\centerdot+\left(\frac{\mathrm{1}}{\mathrm{17}!}−\frac{\mathrm{1}}{\mathrm{18}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{18}!} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}!} \\ $$

Answered by robocop last updated on 14/Feb/17

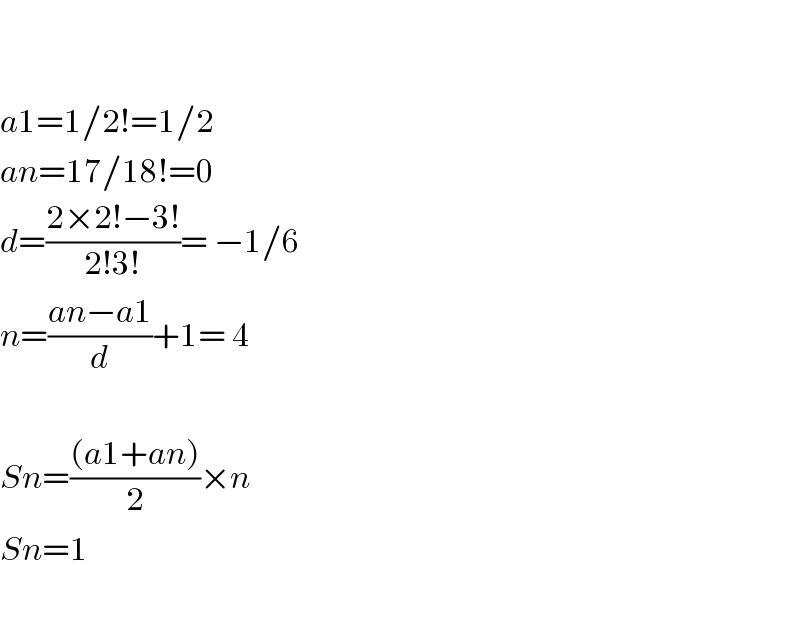
a1=1/2!=1/2 an=17/18!=0 d=((2×2!−3!)/(2!3!))= −1/6 n=((an−a1)/d)+1= 4 Sn=(((a1+an))/2)×n Sn=1

$$ \\ $$$$ \\ $$$${a}\mathrm{1}=\mathrm{1}/\mathrm{2}!=\mathrm{1}/\mathrm{2} \\ $$$${an}=\mathrm{17}/\mathrm{18}!=\mathrm{0} \\ $$$${d}=\frac{\mathrm{2}×\mathrm{2}!−\mathrm{3}!}{\mathrm{2}!\mathrm{3}!}=\:−\mathrm{1}/\mathrm{6} \\ $$$${n}=\frac{{an}−{a}\mathrm{1}}{{d}}+\mathrm{1}=\:\mathrm{4} \\ $$$$ \\ $$$${Sn}=\frac{\left({a}\mathrm{1}+{an}\right)}{\mathrm{2}}×{n} \\ $$$${Sn}=\mathrm{1} \\ $$$$ \\ $$

Commented by FilupS last updated on 15/Feb/17

this method wont work because a sequence of factorials is product based and they grow exponentially larger. i.e. let S=n!+(n+1)!+(n+2)!+... if d=t_2 −t_1 =t_3 −t_2 ∴ d=(n+1)!−n!=(n+2)!−(n+1)! =n!∙((n+1)−1)=(n+1)!∙((n+2)−1) =n!∙(n)=(n+1)!∙(n+1) =n!∙(n)=(n)!∙(n+1)^2 this is a clear contradiction, because the RHS is larger by a factor of (((n+1)^2 )/n), rather than being larger than a common difference.

$$\mathrm{this}\:\mathrm{method}\:\mathrm{wont}\:\mathrm{work}\:\mathrm{because}\:\mathrm{a}\:\mathrm{sequence} \\ $$$$\mathrm{of}\:\mathrm{factorials}\:\mathrm{is}\:\mathrm{product}\:\mathrm{based}\:\mathrm{and}\:\mathrm{they} \\ $$$$\mathrm{grow}\:\mathrm{exponentially}\:\mathrm{larger}.\:\mathrm{i}.\mathrm{e}. \\ $$$$ \\ $$$$\mathrm{let}\:{S}={n}!+\left({n}+\mathrm{1}\right)!+\left({n}+\mathrm{2}\right)!+... \\ $$$$\mathrm{if}\:{d}={t}_{\mathrm{2}} −{t}_{\mathrm{1}} ={t}_{\mathrm{3}} −{t}_{\mathrm{2}} \\ $$$$\therefore\:{d}=\left({n}+\mathrm{1}\right)!−{n}!=\left({n}+\mathrm{2}\right)!−\left({n}+\mathrm{1}\right)! \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left(\left({n}+\mathrm{1}\right)−\mathrm{1}\right)=\left({n}+\mathrm{1}\right)!\centerdot\left(\left({n}+\mathrm{2}\right)−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left({n}\right)=\left({n}+\mathrm{1}\right)!\centerdot\left({n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:={n}!\centerdot\left({n}\right)=\left({n}\right)!\centerdot\left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{clear}\:\mathrm{contradiction},\:\mathrm{because}\:\mathrm{the} \\ $$$$\mathrm{RHS}\:\mathrm{is}\:\mathrm{larger}\:\mathrm{by}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of}\:\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}},\: \\ $$$$\mathrm{rather}\:\mathrm{than}\:\mathrm{being}\:\mathrm{larger}\:\mathrm{than}\:\mathrm{a}\:\mathrm{common} \\ $$$$\mathrm{difference}. \\ $$

Commented by robocop last updated on 15/Feb/17

1−(1/(18!))=((18!−1)/(18!))=1

$$ \\ $$$$ \\ $$$$ \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}!}=\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}=\mathrm{1} \\ $$

Commented by FilupS last updated on 16/Feb/17

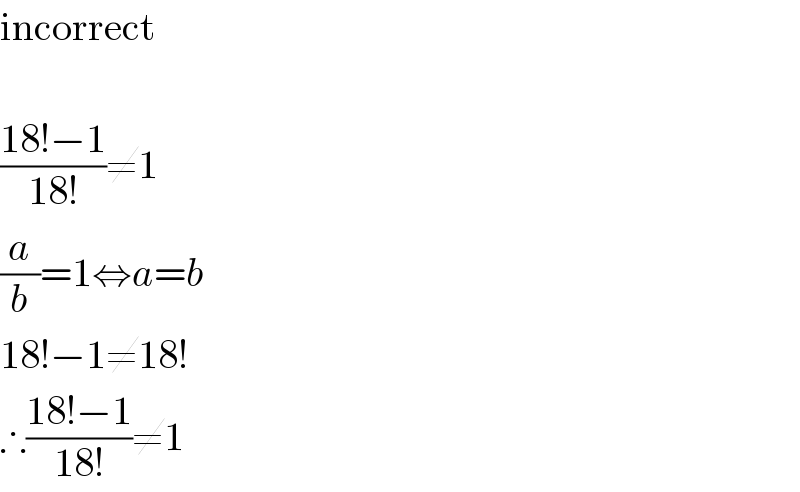
incorrect ((18!−1)/(18!))≠1 (a/b)=1⇔a=b 18!−1≠18! ∴((18!−1)/(18!))≠1

$$\mathrm{incorrect} \\ $$$$\: \\ $$$$\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}\neq\mathrm{1} \\ $$$$\frac{{a}}{{b}}=\mathrm{1}\Leftrightarrow{a}={b} \\ $$$$\mathrm{18}!−\mathrm{1}\neq\mathrm{18}! \\ $$$$\therefore\frac{\mathrm{18}!−\mathrm{1}}{\mathrm{18}!}\neq\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com