
Question Number 104998 by mathocean1 last updated on 25/Jul/20

Commented by mathocean1 last updated on 25/Jul/20
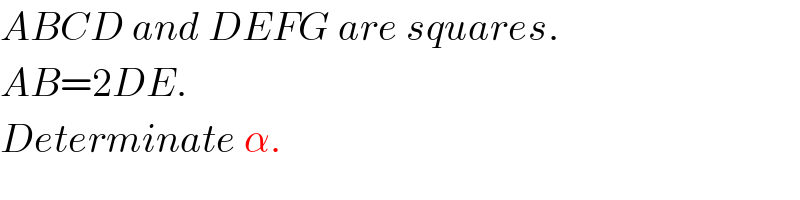
$${ABCD}\:{and}\:{DEFG}\:{are}\:{squares}. \\ $$$${AB}=\mathrm{2}{DE}. \\ $$$${Determinate}\:\alpha. \\ $$
Commented by ajfour last updated on 25/Jul/20

$${many}\:{unnecessary}\:{constructions} \\ $$$${make}\:{question}\:{confusing}.. \\ $$
Answered by 1549442205PVT last updated on 25/Jul/20
Commented by 1549442205PVT last updated on 25/Jul/20

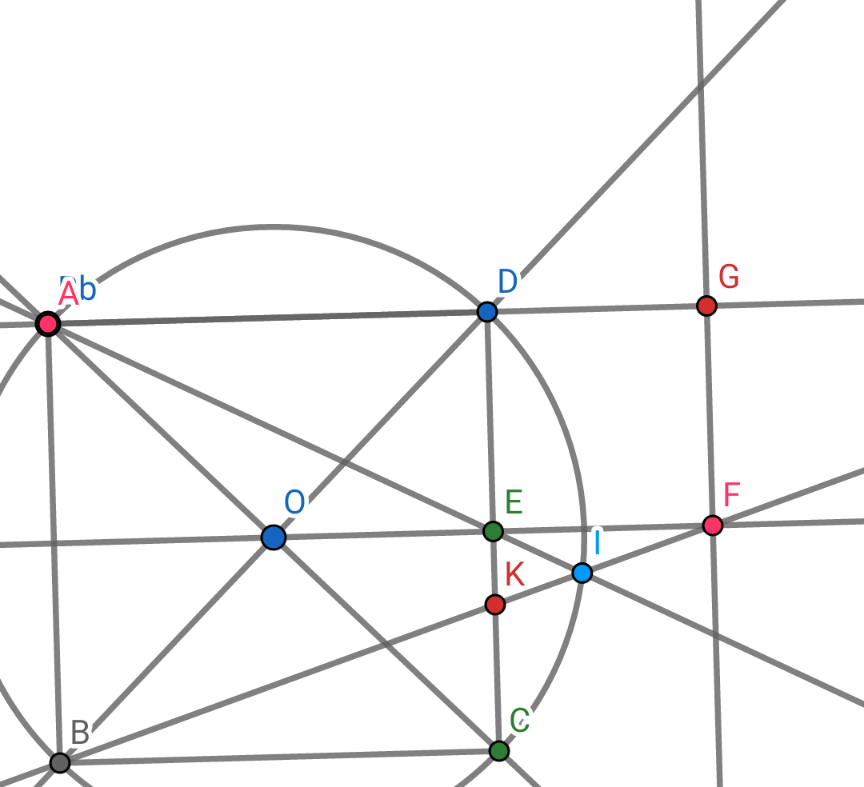
$$ \\ $$$$\mathrm{Putting}\:\mathrm{AB}=\mathrm{2a}\Rightarrow\mathrm{DE}=\mathrm{a}.\mathrm{Denote}\:\mathrm{by}\:\mathrm{I} \\ $$$$\mathrm{intersection}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ray}\:\mathrm{AE}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\left(\mathrm{O}\right) \\ $$$$\mathrm{From}\:\mathrm{Pithago}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{AE}=\sqrt{\mathrm{AD}^{\mathrm{2}} +\mathrm{DE}^{\mathrm{2}} }\:=\mathrm{a}\sqrt{\mathrm{5}}.\left(\mathrm{1}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{formular}\:\mathrm{in}\:\mathrm{circle}\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{EC}.\mathrm{ED}=\mathrm{EA}.\mathrm{EI}\Leftrightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{a}\sqrt{\mathrm{5}}.\mathrm{EI} \\ $$$$\Rightarrow\mathrm{EI}=\frac{\mathrm{a}}{\sqrt{\mathrm{5}}}. \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{EI}}{\mathrm{ED}}=\frac{\mathrm{EF}}{\mathrm{AE}}=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}.\mathrm{It}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\Delta\mathrm{AOE}\backsimeq\Delta\mathrm{FIE}\left(\mathrm{s}.\mathrm{a}.\mathrm{s}\right)\Rightarrow\widehat {\mathrm{EIF}}=\widehat {\mathrm{AOE}}=\mathrm{135}° \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\widehat {\mathrm{AIB}}=\widehat {\mathrm{ADB}}=\mathrm{45}° \\ $$$$\Rightarrow\widehat {\mathrm{AIB}}+\widehat {\mathrm{EIF}}=\mathrm{45}°+\mathrm{135}°=\mathrm{180}°.\mathrm{This}\: \\ $$$$\mathrm{shows}\:\mathrm{that}\:\mathrm{E},\mathrm{I},\mathrm{B}\:\mathrm{are}\:\mathrm{colinear}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$
Commented by mathocean1 last updated on 25/Jul/20

$${thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 25/Jul/20
Commented by mr W last updated on 25/Jul/20

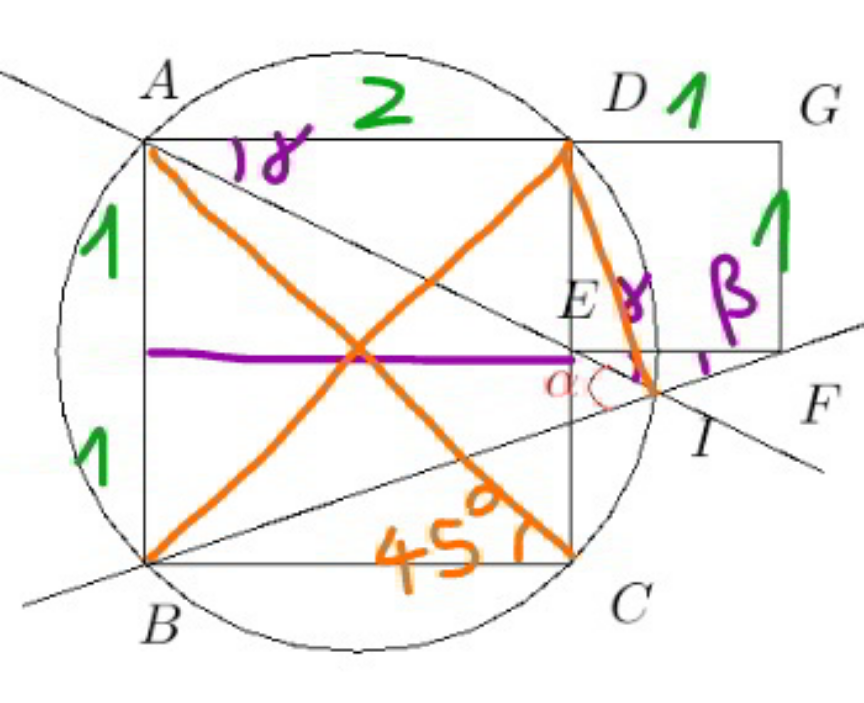
$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha=\beta+\gamma \\ $$$$\mathrm{tan}\:\alpha=\mathrm{tan}\:\left(\beta+\gamma\right)=\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{1} \\ $$$$\Rightarrow\alpha=\mathrm{45}° \\ $$$$\angle{AIB}=\alpha=\angle{ACB}=\mathrm{45}° \\ $$$$\Rightarrow{I}\:{is}\:{on}\:{the}\:{circle}. \\ $$$$ \\ $$$${BD}\:{is}\:{diameter}\:{of}\:{circle}, \\ $$$$\Rightarrow\Delta{BDI}\:{is}\:{right}\:{angled}\:{triangle}, \\ $$$$\Rightarrow{DI}\bot{BI} \\ $$
