
Question Number 105018 by bemath last updated on 25/Jul/20

$$\frac{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}\:+\:\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}\:? \\ $$
Commented by bemath last updated on 25/Jul/20

$${thank}\:{you}\:{all} \\ $$
Answered by som(math1967) last updated on 25/Jul/20
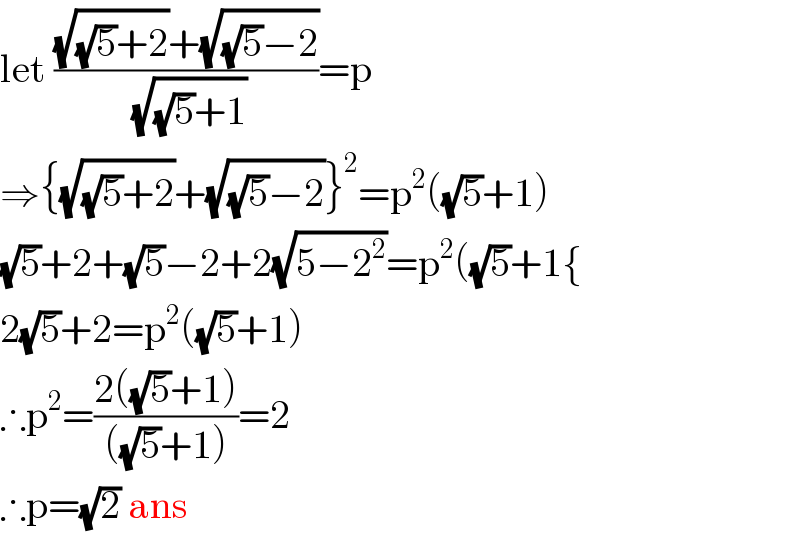
$$\mathrm{let}\:\frac{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}=\mathrm{p} \\ $$$$\Rightarrow\left\{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}\right\}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}+\mathrm{1}\right) \\ $$$$\sqrt{\mathrm{5}}+\mathrm{2}+\sqrt{\mathrm{5}}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}−\mathrm{2}^{\mathrm{2}} }=\mathrm{p}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}+\mathrm{1}\left\{\right.\right. \\ $$$$\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}=\mathrm{p}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}+\mathrm{1}\right) \\ $$$$\therefore\mathrm{p}^{\mathrm{2}} =\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}=\mathrm{2} \\ $$$$\therefore\mathrm{p}=\sqrt{\mathrm{2}}\:\mathrm{ans} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jul/20
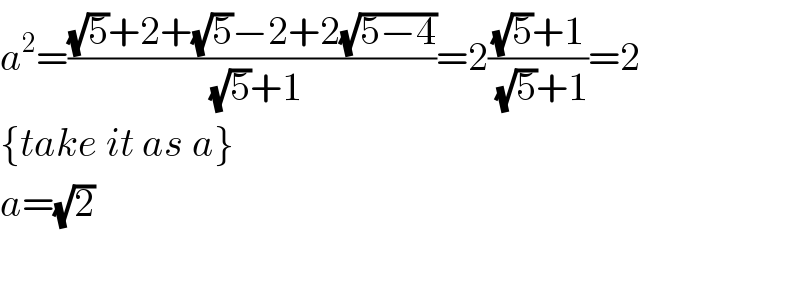
$${a}^{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}+\mathrm{2}+\sqrt{\mathrm{5}}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}−\mathrm{4}}}{\sqrt{\mathrm{5}}+\mathrm{1}}=\mathrm{2}\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\sqrt{\mathrm{5}}+\mathrm{1}}=\mathrm{2} \\ $$$$\left\{{take}\:{it}\:{as}\:{a}\right\} \\ $$$${a}=\sqrt{\mathrm{2}} \\ $$$$ \\ $$
Answered by john santu last updated on 25/Jul/20
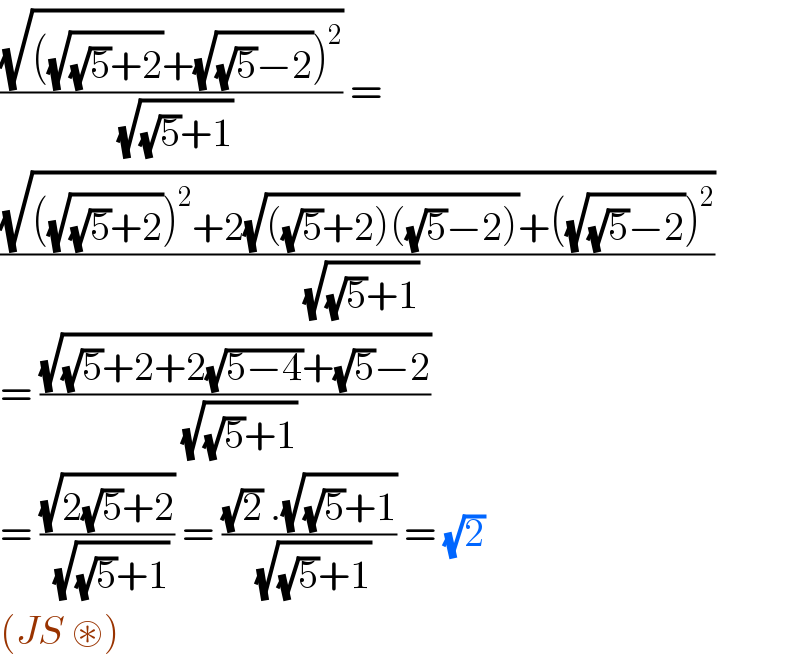
$$\frac{\sqrt{\left(\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}+\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}\right)^{\mathrm{2}} }}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}\:=\: \\ $$$$\frac{\sqrt{\left(\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}+\left(\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}\right)^{\mathrm{2}} }}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}} \\ $$$$=\:\frac{\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}−\mathrm{4}}+\sqrt{\mathrm{5}}−\mathrm{2}}}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}} \\ $$$$=\:\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}}}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}\:=\:\frac{\sqrt{\mathrm{2}}\:.\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}{\sqrt{\sqrt{\mathrm{5}}+\mathrm{1}}}\:=\:\sqrt{\mathrm{2}}\: \\ $$$$\left({JS}\:\circledast\right)\: \\ $$
