
Question Number 105026 by mohammad17 last updated on 25/Jul/20

Answered by john santu last updated on 25/Jul/20
![Q−3 (dx/dy) = (y^2 /2)−(1/(2y^2 )) = ((y^4 −1)/(2y^2 )) length of curve = ∫_a ^(1.5a) (√(1+((dx/dy))^2 )) dy = ∫_a ^(1.5a) (√(1+(((y^4 −1)/(2y^2 )))^2 )) dy = ∫_a ^(1.5a) (√((y^8 +4y^4 −2y^4 +1)/(4y^4 ))) dy = ∫_a ^(1.5a) (1/(2y^2 )) (√((y^4 +1)^2 )) dy =∫_a ^(1.5a) ((y^4 +1)/(2y^2 )) dy = [(1/6)y^3 −(1/(2y))]_a ^(1.5a) (JS ♠⧫)](Q105030.png)
$${Q}−\mathrm{3} \\ $$$$\frac{{dx}}{{dy}}\:=\:\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }\:=\:\frac{{y}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} } \\ $$$${length}\:{of}\:{curve}\: \\ $$$$=\:\underset{{a}} {\overset{\mathrm{1}.\mathrm{5}{a}} {\int}}\sqrt{\mathrm{1}+\left(\frac{{dx}}{{dy}}\right)^{\mathrm{2}} }\:{dy}\: \\ $$$$=\:\underset{{a}} {\overset{\mathrm{1}.\mathrm{5}{a}} {\int}}\sqrt{\mathrm{1}+\left(\frac{{y}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{dy}\: \\ $$$$=\:\underset{{a}} {\overset{\mathrm{1}.\mathrm{5}{a}} {\int}}\sqrt{\frac{{y}^{\mathrm{8}} +\mathrm{4}{y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}}{\mathrm{4}{y}^{\mathrm{4}} }}\:{dy} \\ $$$$=\:\underset{{a}} {\overset{\mathrm{1}.\mathrm{5}{a}} {\int}}\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }\:\sqrt{\left({y}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dy}\: \\ $$$$=\underset{{a}} {\overset{\mathrm{1}.\mathrm{5}{a}} {\int}}\frac{{y}^{\mathrm{4}} +\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }\:{dy}\:=\:\left[\frac{\mathrm{1}}{\mathrm{6}}{y}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}{y}}\right]_{{a}} ^{\mathrm{1}.\mathrm{5}{a}} \\ $$$$\left({JS}\:\spadesuit\blacklozenge\right) \\ $$
Commented by mohammad17 last updated on 25/Jul/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jul/20
![2)∫_0 ^a (√(4−9x^2 ))dx =[((3x)/2)(√(4−9x^2 ))]_0 ^a −[(((2)^2 )/2)sin^(−1) ((3x)/2)]_0 ^a =((3a)/2)(√(4−9a^2 ))−2sin^(−1) ((3a)/2)](Q105031.png)
$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{{a}} \sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }{dx} \\ $$$$=\left[\frac{\mathrm{3}{x}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{9}{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{{a}} −\left[\frac{\left(\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{\mathrm{3}{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{{a}} \\ $$$$=\frac{\mathrm{3}{a}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{9}{a}^{\mathrm{2}} }−\mathrm{2}{sin}^{−\mathrm{1}} \frac{\mathrm{3}{a}}{\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 25/Jul/20

$${thank}\:{you}\:{sir} \\ $$
Answered by john santu last updated on 25/Jul/20
![Q−4.(1) ∫(ax+3a)^(a+3) dx = (1/a)∫(ax+3a)^(a+3) d(ax+3a) [ b = ax+3a ] (1/a)∫ b^(a+3) db = (b^(a+4) /(a(a+4))) + c = (((ax+3a)^(a+4) )/(a^2 +4a)) + c](Q105035.png)
$${Q}−\mathrm{4}.\left(\mathrm{1}\right) \\ $$$$\int\left({ax}+\mathrm{3}{a}\right)^{{a}+\mathrm{3}} \:{dx}\:=\:\frac{\mathrm{1}}{{a}}\int\left({ax}+\mathrm{3}{a}\right)^{{a}+\mathrm{3}} {d}\left({ax}+\mathrm{3}{a}\right) \\ $$$$\left[\:{b}\:=\:{ax}+\mathrm{3}{a}\:\right]\: \\ $$$$\frac{\mathrm{1}}{{a}}\int\:{b}^{{a}+\mathrm{3}} \:{db}\:=\:\frac{{b}^{{a}+\mathrm{4}} }{{a}\left({a}+\mathrm{4}\right)}\:+\:{c}\: \\ $$$$=\:\frac{\left({ax}+\mathrm{3}{a}\right)^{{a}+\mathrm{4}} }{{a}^{\mathrm{2}} +\mathrm{4}{a}}\:+\:{c}\: \\ $$
Answered by mathmax by abdo last updated on 25/Jul/20
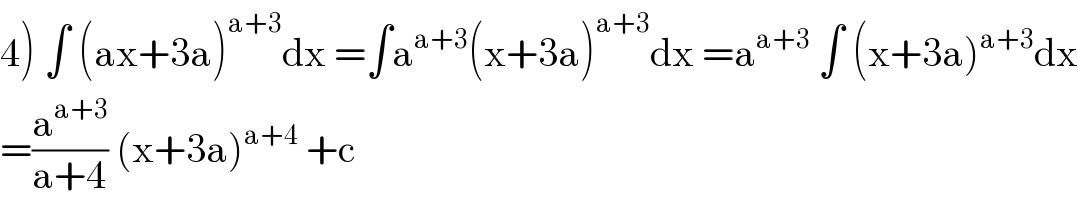
$$\left.\mathrm{4}\right)\:\int\:\left(\mathrm{ax}+\mathrm{3a}\right)^{\mathrm{a}+\mathrm{3}} \mathrm{dx}\:=\int\mathrm{a}^{\mathrm{a}+\mathrm{3}} \left(\mathrm{x}+\mathrm{3a}\right)^{\mathrm{a}+\mathrm{3}} \mathrm{dx}\:=\mathrm{a}^{\mathrm{a}+\mathrm{3}} \:\int\:\left(\mathrm{x}+\mathrm{3a}\right)^{\mathrm{a}+\mathrm{3}} \mathrm{dx} \\ $$$$=\frac{\mathrm{a}^{\mathrm{a}+\mathrm{3}} }{\mathrm{a}+\mathrm{4}}\:\left(\mathrm{x}+\mathrm{3a}\right)^{\mathrm{a}+\mathrm{4}} \:+\mathrm{c} \\ $$
Commented by bemath last updated on 26/Jul/20
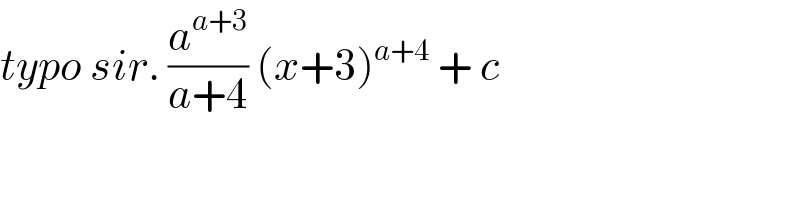
$${typo}\:{sir}.\:\frac{{a}^{{a}+\mathrm{3}} }{{a}+\mathrm{4}}\:\left({x}+\mathrm{3}\right)^{{a}+\mathrm{4}} \:+\:{c}\: \\ $$
Commented by mathmax by abdo last updated on 26/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 25/Jul/20
![2) I =∫_0 ^a (√(4−9x^2 ))dx =2 ∫_0 ^a (√(1−(9/4)x^2 ))dx we do the changement (3/2)x =sint ⇒ I =2 ∫_0 ^(arcsin(((3a)/2))) (√(1−sin^2 t))×(2/3) cost dt =(4/3) ∫_0 ^(arcsin(((3a)/2))) cos^2 t dt =(2/3)∫_0 ^(arcsin(((3a)/2))) (1+cos(2t))dt =(2/3) arcsin(((3a)/2)) +(1/3)[sin(2t)]_o ^(arcsin(((3a)/2))) =(2/3) arcsin(((3a)/2)) +(2/3)[sint (√(1−sin^2 t))]_0 ^(arcsin(((3a)/2))) =(2/3) arcsin(((3a)/2))+(2/3){((3a)/2)(√(1−((9a^2 )/4)))} =(2/3) arcsin(((3a)/2)) +a(√(1−((9a^2 )/4)))](Q105052.png)
$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{a}} \sqrt{\mathrm{4}−\mathrm{9x}^{\mathrm{2}} }\mathrm{dx}\:\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{a}} \sqrt{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}\:=\mathrm{sint}\:\Rightarrow\:\mathrm{I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)} \sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{t}}×\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{cost}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)} \mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)} \:\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\mathrm{o}} ^{\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)\:+\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{sint}\:\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\right]_{\mathrm{0}} ^{\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)+\frac{\mathrm{2}}{\mathrm{3}}\left\{\frac{\mathrm{3a}}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{9a}^{\mathrm{2}} }{\mathrm{4}}}\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{arcsin}\left(\frac{\mathrm{3a}}{\mathrm{2}}\right)\:+\mathrm{a}\sqrt{\mathrm{1}−\frac{\mathrm{9a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$
