
Question Number 105039 by bemath last updated on 25/Jul/20

$$\left(\mathrm{1}\right)\:\int\:\frac{{dx}}{{x}^{\mathrm{6}} −\mathrm{64}} \\ $$$$\left(\mathrm{2}\right)\:{y}'\:+\:{y}\:\mathrm{tan}\:{x}\:=\:\mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$
Answered by bobhans last updated on 25/Jul/20
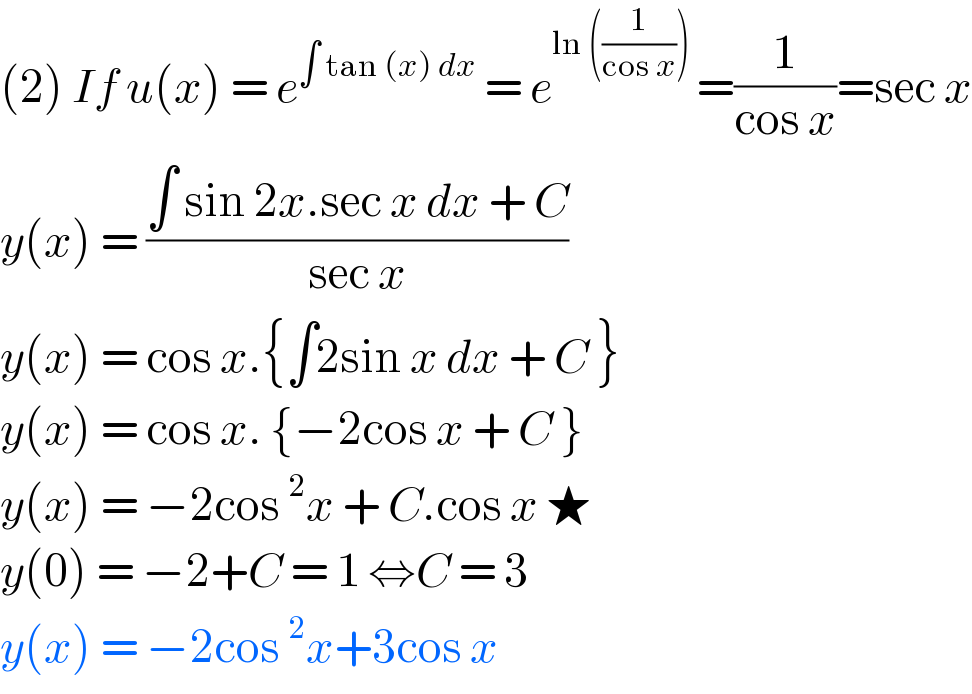
$$\left(\mathrm{2}\right)\:{If}\:{u}\left({x}\right)\:=\:{e}^{\int\:\mathrm{tan}\:\left({x}\right)\:{dx}} \:=\:{e}^{\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{cos}\:{x}}\right)\:} =\frac{\mathrm{1}}{\mathrm{cos}\:{x}}=\mathrm{sec}\:{x} \\ $$$${y}\left({x}\right)\:=\:\frac{\int\:\mathrm{sin}\:\mathrm{2}{x}.\mathrm{sec}\:{x}\:{dx}\:+\:{C}}{\mathrm{sec}\:{x}} \\ $$$${y}\left({x}\right)\:=\:\mathrm{cos}\:{x}.\left\{\int\mathrm{2sin}\:{x}\:{dx}\:+\:{C}\:\right\} \\ $$$${y}\left({x}\right)\:=\:\mathrm{cos}\:{x}.\:\left\{−\mathrm{2cos}\:{x}\:+\:{C}\:\right\} \\ $$$${y}\left({x}\right)\:=\:−\mathrm{2cos}\:^{\mathrm{2}} {x}\:+\:{C}.\mathrm{cos}\:{x}\:\bigstar \\ $$$${y}\left(\mathrm{0}\right)\:=\:−\mathrm{2}+{C}\:=\:\mathrm{1}\:\Leftrightarrow{C}\:=\:\mathrm{3} \\ $$$${y}\left({x}\right)\:=\:−\mathrm{2cos}\:^{\mathrm{2}} {x}+\mathrm{3cos}\:{x}\: \\ $$
Answered by mathmax by abdo last updated on 25/Jul/20
![1) complex method we decompose F(z) =(1/(z^6 −64)) ⇒ z^6 =64 let z =re^(iθ) so e ⇒r^6 e^(i6θ) =64 e^(i(2kπ)) ⇒r =^6 (√(64)) =2 θ =((kπ)/3) and k∈[[0,5]] so the roots are z_k =2e^(i((kπ)/3)) and 0≤k≤5 ⇒F(z) =(1/(Π_(k=0) ^5 (z−z_k ))) =Σ_(k=0) ^5 (a_k /(z−z_k )) with a_k =(1/(6z_k ^5 )) =(z_k /(6(64))) =(z_k /(384)) ⇒F(z) =(1/(384)) Σ_(k=0) ^5 (z_k /(z−z_k )) ⇒∫ F(z)dz =(1/(384)) Σ_(k=0) ^5 z_k ∫ (dz/(z−2e^((ikπ)/3) )) =(1/(384)) Σ_(k=0) ^5 (2e^((ikπ)/3) )ln(z−2e^((ikπ)/3) ) +C](Q105049.png)
$$\left.\mathrm{1}\right)\:\mathrm{complex}\:\mathrm{method}\:\:\mathrm{we}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} −\mathrm{64}}\:\Rightarrow \\ $$$$\mathrm{z}^{\mathrm{6}} \:=\mathrm{64}\:\:\:\mathrm{let}\:\mathrm{z}\:=\mathrm{re}^{\mathrm{i}\theta} \:\:\:\:\:\mathrm{so}\:\mathrm{e}\:\Rightarrow\mathrm{r}^{\mathrm{6}} \:\mathrm{e}^{\mathrm{i6}\theta} \:=\mathrm{64}\:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}\pi\right)} \:\Rightarrow\mathrm{r}\:=^{\mathrm{6}} \sqrt{\mathrm{64}}\:=\mathrm{2} \\ $$$$\theta\:=\frac{\mathrm{k}\pi}{\mathrm{3}}\:\:\mathrm{and}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{5}\right]\right]\:\mathrm{so}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{z}_{\mathrm{k}} =\mathrm{2e}^{\mathrm{i}\frac{\mathrm{k}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{k}\leqslant\mathrm{5} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\:\mathrm{with}\:\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{6z}_{\mathrm{k}} ^{\mathrm{5}} }\:=\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{6}\left(\mathrm{64}\right)}\:=\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{384}} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\mathrm{384}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \:\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow\int\:\mathrm{F}\left(\mathrm{z}\right)\mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{384}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \mathrm{z}_{\mathrm{k}} \:\int\:\:\frac{\mathrm{dz}}{\mathrm{z}−\mathrm{2e}^{\frac{\mathrm{ik}\pi}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{384}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \:\left(\mathrm{2e}^{\frac{\mathrm{ik}\pi}{\mathrm{3}}} \right)\mathrm{ln}\left(\mathrm{z}−\mathrm{2e}^{\frac{\mathrm{ik}\pi}{\mathrm{3}}} \right)\:\:+\mathrm{C} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jul/20
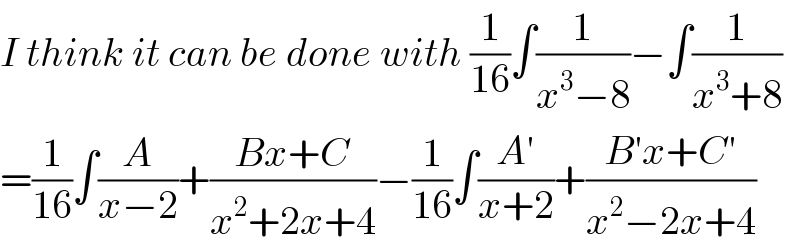
$${I}\:{think}\:{it}\:{can}\:{be}\:{done}\:{with}\:\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{8}}−\int\frac{\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{A}}{{x}−\mathrm{2}}+\frac{{Bx}+{C}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{A}'}{{x}+\mathrm{2}}+\frac{{B}'{x}+{C}'}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 26/Jul/20
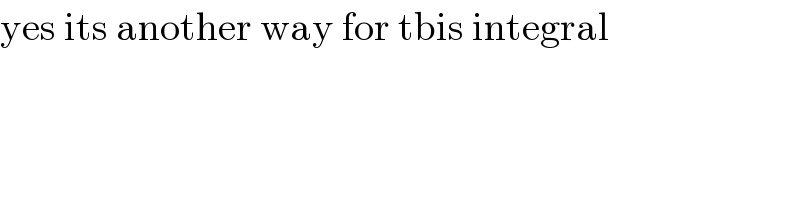
$$\mathrm{yes}\:\mathrm{its}\:\mathrm{another}\:\mathrm{way}\:\mathrm{for}\:\mathrm{tbis}\:\mathrm{integral} \\ $$
Answered by mathmax by abdo last updated on 25/Jul/20
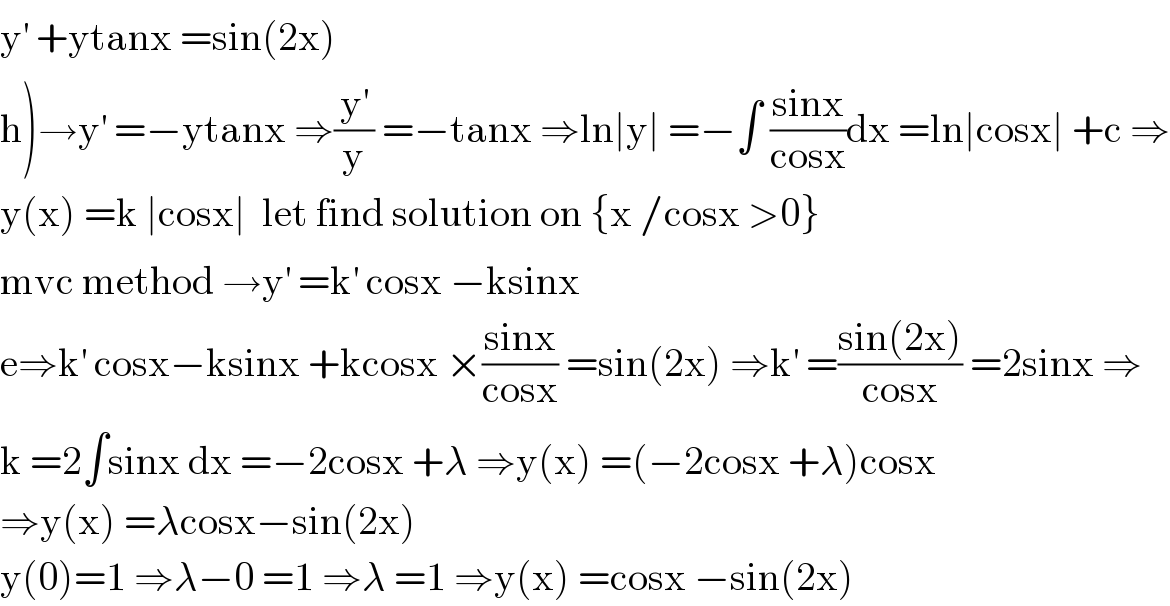
$$\mathrm{y}^{'} \:+\mathrm{ytanx}\:=\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\left.\mathrm{h}\right)\rightarrow\mathrm{y}^{'} \:=−\mathrm{ytanx}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\mathrm{tanx}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\int\:\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx}\:=\mathrm{ln}\mid\mathrm{cosx}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\:\mid\mathrm{cosx}\mid\:\:\mathrm{let}\:\mathrm{find}\:\mathrm{solution}\:\mathrm{on}\:\left\{\mathrm{x}\:/\mathrm{cosx}\:>\mathrm{0}\right\} \\ $$$$\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{cosx}\:−\mathrm{ksinx}\: \\ $$$$\mathrm{e}\Rightarrow\mathrm{k}^{'} \:\mathrm{cosx}−\mathrm{ksinx}\:+\mathrm{kcosx}\:×\frac{\mathrm{sinx}}{\mathrm{cosx}}\:=\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{cosx}}\:=\mathrm{2sinx}\:\Rightarrow \\ $$$$\mathrm{k}\:=\mathrm{2}\int\mathrm{sinx}\:\mathrm{dx}\:=−\mathrm{2cosx}\:+\lambda\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\left(−\mathrm{2cosx}\:+\lambda\right)\mathrm{cosx} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\lambda\mathrm{cosx}−\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\lambda−\mathrm{0}\:=\mathrm{1}\:\Rightarrow\lambda\:=\mathrm{1}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{cosx}\:−\mathrm{sin}\left(\mathrm{2x}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jul/20
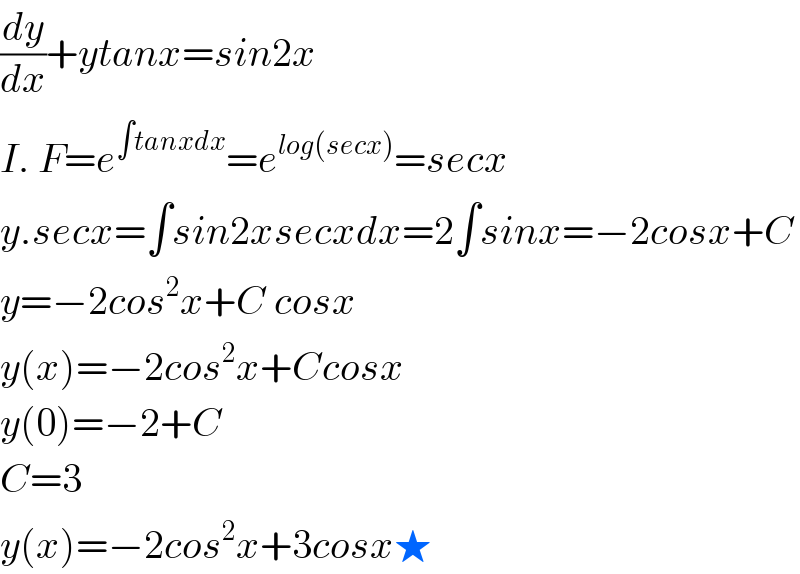
$$\frac{{dy}}{{dx}}+{ytanx}={sin}\mathrm{2}{x} \\ $$$${I}.\:{F}={e}^{\int{tanxdx}} ={e}^{{log}\left({secx}\right)} ={secx} \\ $$$${y}.{secx}=\int{sin}\mathrm{2}{xsecxdx}=\mathrm{2}\int{sinx}=−\mathrm{2}{cosx}+{C} \\ $$$${y}=−\mathrm{2}{cos}^{\mathrm{2}} {x}+{C}\:{cosx} \\ $$$${y}\left({x}\right)=−\mathrm{2}{cos}^{\mathrm{2}} {x}+{Ccosx} \\ $$$${y}\left(\mathrm{0}\right)=−\mathrm{2}+{C} \\ $$$${C}=\mathrm{3} \\ $$$${y}\left({x}\right)=−\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{3}{cosx}\bigstar \\ $$
Answered by OlafThorendsen last updated on 25/Jul/20
![(1) R(x) = (1/(x^6 −1)) R(x) = (1/((x−1)(x+1)(x^2 −x+1)(x^2 −x+1))) ∫R(x)dx = ∫((1/(6(x−1)))−(1/(6(x+1)))+((x−2)/(6(x^2 −x+1)))−((x+2)/(6(x^2 +x+1))))dx = (1/6)ln∣((x−1)/(x+1))∣ +(1/(12))∫((2x−1)/(x^2 −x+1))dx−(1/(12))∫((2x+1)/(x^2 +x+1))dx −(1/4)∫(dx/(x^2 −x+1))−(1/4)∫(dx/(x^2 +x+1)) =(1/6)ln∣((x−1)/(x+1))∣+(1/(12))ln∣((x^2 −x+1)/(x^2 +x+1))∣ −(1/3)∫(dx/((4/3)(x−(1/2))^2 +1))−(1/3)∫(dx/((4/3)(x+(1/2))^2 +1)) =(1/6)ln∣((x−1)/(x+1))∣+(1/(12))ln∣((x^2 −x+1)/(x^2 +x+1))∣ −(1/(2(√3)))arctan[(2/(√3))(x−(1/2))]−(1/(2(√3)))arctan[(2/(√3))(x+(1/2))] arctanu+arctanv = arctan((u+v)/(1−uv)) u = (2/(√3))(x−(1/2)) and v = (2/(√3))(x+(1/2)) ((u+v)/(1−uv)) = (((4/(√3))x)/(1−(4/3)(x^2 −(1/4)))) = (((√3)x)/(1−x^2 )) Finally : ∫R(x)dx = (1/6)ln∣((x−1)/(x+1))∣+(1/(12))ln∣((x^2 −x+1)/(x^2 +x+1))∣−(1/(2(√3)))arctan(((√3)x)/(1−x^2 ))+C](Q105067.png)
$$\left(\mathrm{1}\right)\:\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{6}} −\mathrm{1}} \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$$\int\mathrm{R}\left({x}\right){dx}\:= \\ $$$$\int\left(\frac{\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}+\frac{{x}−\mathrm{2}}{\mathrm{6}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}−\frac{{x}+\mathrm{2}}{\mathrm{6}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}\right){dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid \\ $$$$+\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\frac{\mathrm{4}}{\mathrm{3}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\frac{\mathrm{4}}{\mathrm{3}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left[\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left[\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right] \\ $$$$\mathrm{arctan}{u}+\mathrm{arctan}{v}\:=\:\mathrm{arctan}\frac{{u}+{v}}{\mathrm{1}−{uv}} \\ $$$${u}\:=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{and}\:{v}\:=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{{u}+{v}}{\mathrm{1}−{uv}}\:=\:\frac{\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}{x}}{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)}\:=\:\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{Finally}\:: \\ $$$$\int\mathrm{R}\left({x}\right){dx}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{C} \\ $$$$ \\ $$
Commented by bemath last updated on 27/Jul/20
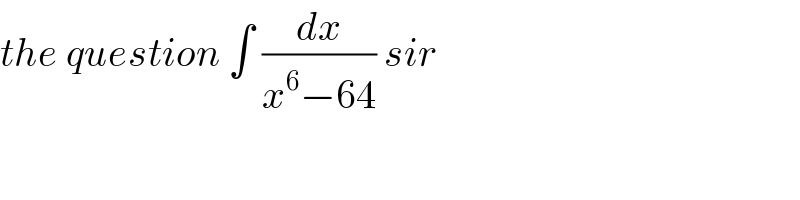
$${the}\:{question}\:\int\:\frac{{dx}}{{x}^{\mathrm{6}} −\mathrm{64}}\:{sir}\: \\ $$
Answered by OlafThorendsen last updated on 25/Jul/20
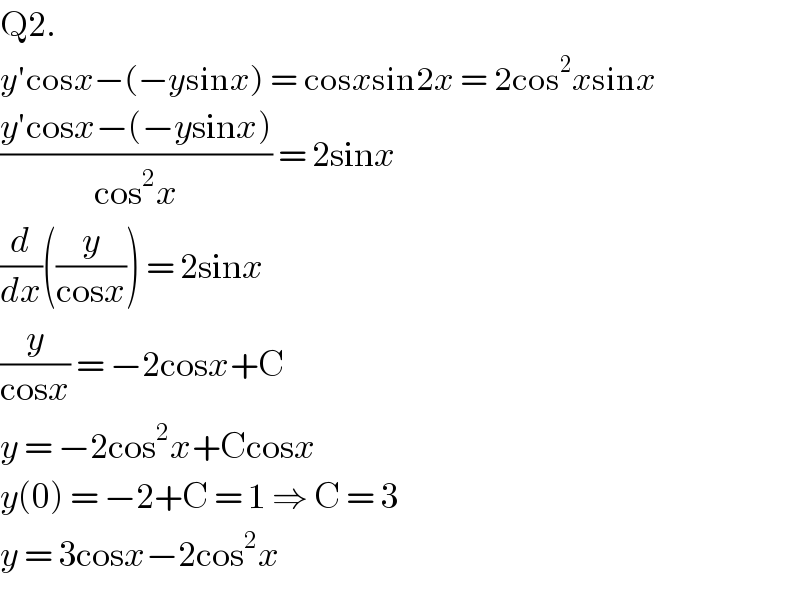
$$\mathrm{Q2}. \\ $$$${y}'\mathrm{cos}{x}−\left(−{y}\mathrm{sin}{x}\right)\:=\:\mathrm{cos}{x}\mathrm{sin2}{x}\:=\:\mathrm{2cos}^{\mathrm{2}} {x}\mathrm{sin}{x} \\ $$$$\frac{{y}'\mathrm{cos}{x}−\left(−{y}\mathrm{sin}{x}\right)}{\mathrm{cos}^{\mathrm{2}} {x}}\:=\:\mathrm{2sin}{x} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{y}}{\mathrm{cos}{x}}\right)\:=\:\mathrm{2sin}{x} \\ $$$$\frac{{y}}{\mathrm{cos}{x}}\:=\:−\mathrm{2cos}{x}+\mathrm{C} \\ $$$${y}\:=\:−\mathrm{2cos}^{\mathrm{2}} {x}+\mathrm{Ccos}{x} \\ $$$${y}\left(\mathrm{0}\right)\:=\:−\mathrm{2}+\mathrm{C}\:=\:\mathrm{1}\:\Rightarrow\:\mathrm{C}\:=\:\mathrm{3} \\ $$$${y}\:=\:\mathrm{3cos}{x}−\mathrm{2cos}^{\mathrm{2}} {x} \\ $$
Answered by bramlex last updated on 26/Jul/20
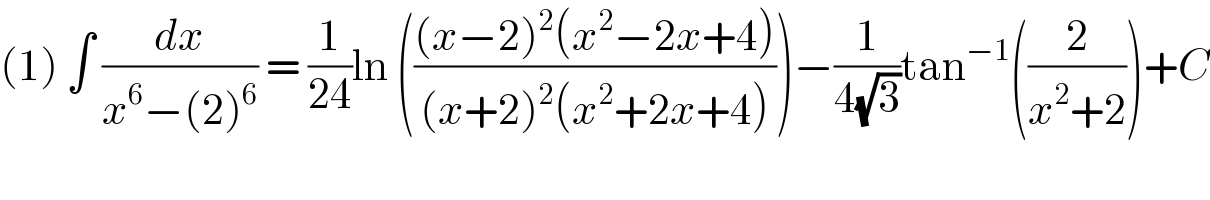
$$\left(\mathrm{1}\right)\:\int\:\frac{{dx}}{{x}^{\mathrm{6}} −\left(\mathrm{2}\right)^{\mathrm{6}} }\:=\:\frac{\mathrm{1}}{\mathrm{24}}\mathrm{ln}\:\left(\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{2}}\right)+{C} \\ $$
