
Question Number 105104 by bemath last updated on 26/Jul/20
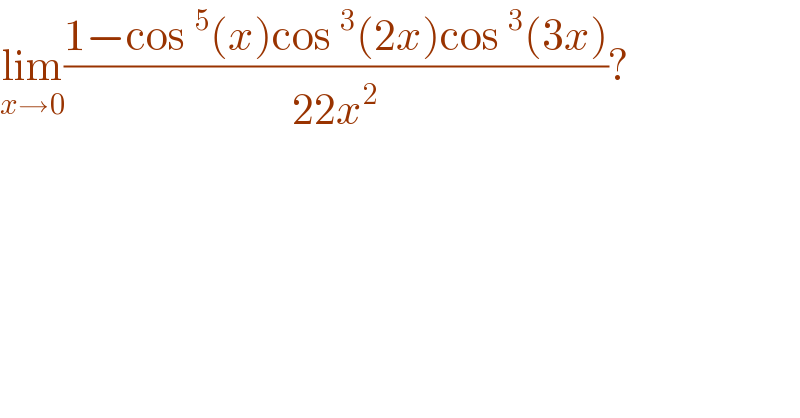
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{5}} \left({x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{2}{x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)}{\mathrm{22}{x}^{\mathrm{2}} }? \\ $$
Answered by bramlex last updated on 26/Jul/20
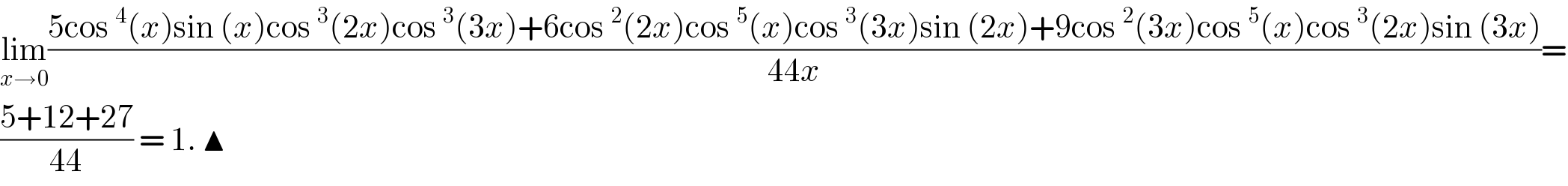
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{5cos}\:^{\mathrm{4}} \left({x}\right)\mathrm{sin}\:\left({x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{2}{x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)+\mathrm{6cos}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)\mathrm{cos}\:^{\mathrm{5}} \left({x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)\mathrm{sin}\:\left(\mathrm{2}{x}\right)+\mathrm{9cos}\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)\mathrm{cos}\:^{\mathrm{5}} \left({x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{2}{x}\right)\mathrm{sin}\:\left(\mathrm{3}{x}\right)}{\mathrm{44}{x}}= \\ $$$$\frac{\mathrm{5}+\mathrm{12}+\mathrm{27}}{\mathrm{44}}\:=\:\mathrm{1}.\:\blacktriangle \\ $$
Answered by bobhans last updated on 26/Jul/20

$$\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:\approx\:\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{5}} \left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{3}} }{\mathrm{22}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{27}{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{22}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\left(\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{6}+\frac{\mathrm{27}}{\mathrm{2}}\right){x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)\right)}{\mathrm{22}{x}^{\mathrm{2}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{6}+\frac{\mathrm{27}}{\mathrm{2}}\right){x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)}{\mathrm{22}{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{44}}{\mathrm{2}\left(\mathrm{22}\right)}\:=\:\mathrm{1} \\ $$$$\left({B}\circledcirc{B}\right) \\ $$
