
Previous in Differential Equation Next in Differential Equation
Question Number 105118 by john santu last updated on 26/Jul/20
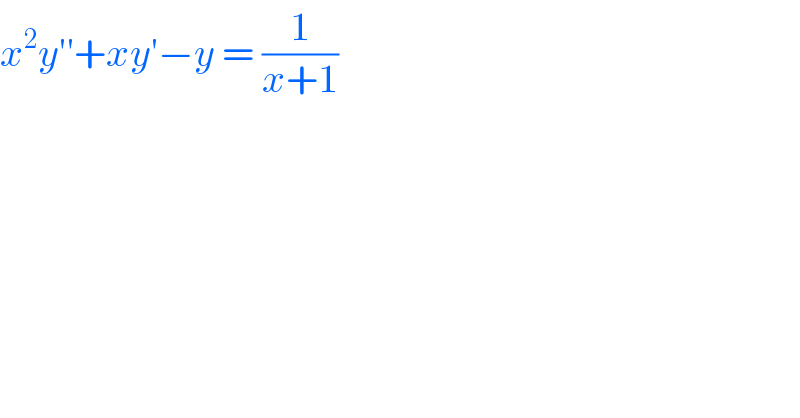
$${x}^{\mathrm{2}} {y}''+{xy}'−{y}\:=\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\: \\ $$
Answered by john santu last updated on 26/Jul/20
![⇒ x^2 y′′+2xy′−xy′ − y = (1/(x+1)) (d/dx)[ x^2 y′−xy ] = (d/dx)[ ln (x+1) ] ∫ (d/dx)[ x^2 y′−xy ] = ∫ (d/dx)[ ln(x+1)] x^2 y′−xy = ln (x+1)+c ((y′)/x) − (y/x^2 ) = ((ln (x+1)+c)/x^3 ) (d/dx)[ (y/x) ] = ((ln (x+1)+c)/x^3 ) ⇔ y = x { ∫ ((ln (x+1)+c)/x^3 ) dx } y = x { −(c/(2x^2 )) + ∫x^(−3) ln (1+x)dx} let J=∫x^(−3) ln (1+x) dx by parts → { ((u=ln (1+x)→du=(1/(1+x))dx)),((v = −(x^(−2) /2))) :} J = −((ln (1+x))/(2x^2 ))+∫(dx/(2x^2 (1+x))) (1/(x^2 (x+1))) = (A/x)+(B/x^2 )+(C/(x+1)) 1 = Ax(x+1)+B(x+1)+Cx^2 x=0→1=B x=−1→1=C x=1→1=2A+2B+C 1 =2A+3 →A=−1 J= −((ln (x+1))/(2x^2 ))+(1/2)∫((1/(x+1))+(1/x^2 )−(1/x))dx J= −((ln (x+1))/(2x^2 ))+(1/2){ln (x+1)−(1/x)−ln x} ∴ y = −(((ln C(x+1))/(2x)))+(x/2){ln (((x+1)/x))−(1/x)}](Q105119.png)
$$\Rightarrow\:{x}^{\mathrm{2}} {y}''+\mathrm{2}{xy}'−{xy}'\:−\:{y}\:=\:\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\frac{{d}}{{dx}}\left[\:{x}^{\mathrm{2}} {y}'−{xy}\:\right]\:=\:\frac{{d}}{{dx}}\left[\:\mathrm{ln}\:\left({x}+\mathrm{1}\right)\:\right] \\ $$$$\int\:\frac{{d}}{{dx}}\left[\:{x}^{\mathrm{2}} {y}'−{xy}\:\right]\:=\:\int\:\frac{{d}}{{dx}}\left[\:\mathrm{ln}\left({x}+\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{2}} {y}'−{xy}\:=\:\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{c} \\ $$$$\frac{{y}'}{{x}}\:−\:\frac{{y}}{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{c}}{{x}^{\mathrm{3}} } \\ $$$$\frac{{d}}{{dx}}\left[\:\frac{{y}}{{x}}\:\right]\:=\:\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{c}}{{x}^{\mathrm{3}} } \\ $$$$\Leftrightarrow\:{y}\:=\:{x}\:\left\{\:\int\:\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{c}}{{x}^{\mathrm{3}} }\:{dx}\:\right\} \\ $$$${y}\:=\:{x}\:\left\{\:−\frac{{c}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\:\int{x}^{−\mathrm{3}} \mathrm{ln}\:\left(\mathrm{1}+{x}\right){dx}\right\} \\ $$$${let}\:{J}=\int{x}^{−\mathrm{3}} \mathrm{ln}\:\left(\mathrm{1}+{x}\right)\:{dx}\: \\ $$$${by}\:{parts}\:\rightarrow\begin{cases}{{u}=\mathrm{ln}\:\left(\mathrm{1}+{x}\right)\rightarrow{du}=\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}}\\{{v}\:=\:−\frac{{x}^{−\mathrm{2}} }{\mathrm{2}}}\end{cases} \\ $$$${J}\:=\:−\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }+\int\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}\:=\:\frac{{A}}{{x}}+\frac{{B}}{{x}^{\mathrm{2}} }+\frac{{C}}{{x}+\mathrm{1}} \\ $$$$\mathrm{1}\:=\:{Ax}\left({x}+\mathrm{1}\right)+{B}\left({x}+\mathrm{1}\right)+{Cx}^{\mathrm{2}} \\ $$$${x}=\mathrm{0}\rightarrow\mathrm{1}={B}\: \\ $$$${x}=−\mathrm{1}\rightarrow\mathrm{1}={C} \\ $$$${x}=\mathrm{1}\rightarrow\mathrm{1}=\mathrm{2}{A}+\mathrm{2}{B}+{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:=\mathrm{2}{A}+\mathrm{3}\:\rightarrow{A}=−\mathrm{1} \\ $$$${J}=\:−\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$${J}=\:−\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{ln}\:\left({x}+\mathrm{1}\right)−\frac{\mathrm{1}}{{x}}−\mathrm{ln}\:{x}\right\} \\ $$$$\therefore\:{y}\:=\:−\left(\frac{\mathrm{ln}\:{C}\left({x}+\mathrm{1}\right)}{\mathrm{2}{x}}\right)+\frac{{x}}{\mathrm{2}}\left\{\mathrm{ln}\:\left(\frac{{x}+\mathrm{1}}{{x}}\right)−\frac{\mathrm{1}}{{x}}\right\} \\ $$
