Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 105132 by mohammad17 last updated on 26/Jul/20

Answered by Dwaipayan Shikari last updated on 26/Jul/20

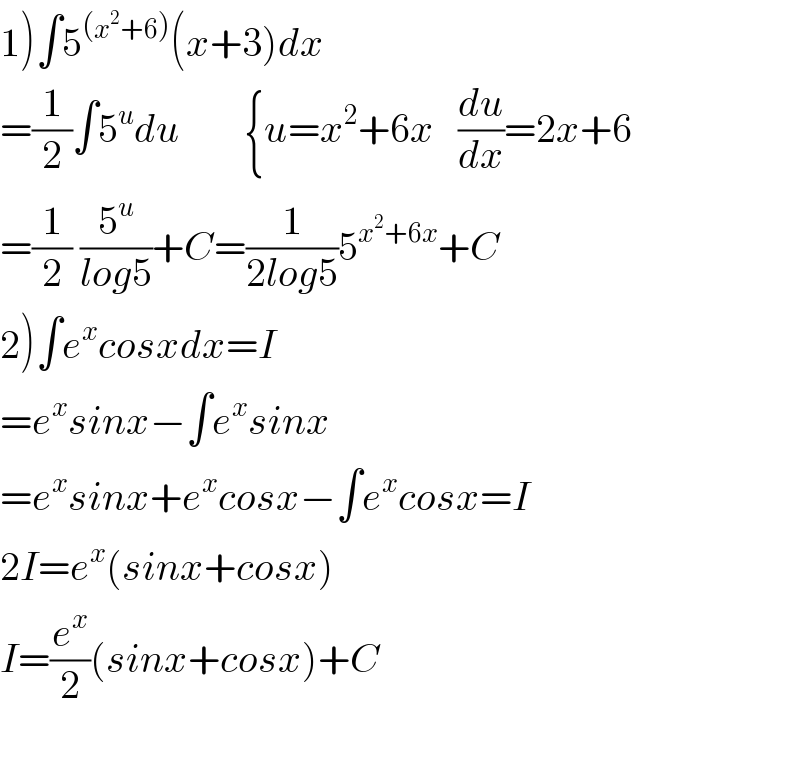
1)∫5^((x^2 +6)) (x+3)dx =(1/2)∫5^u du {u=x^2 +6x (du/dx)=2x+6 =(1/2) (5^u /(log5))+C=(1/(2log5))5^(x^2 +6x) +C 2)∫e^x cosxdx=I =e^x sinx−∫e^x sinx =e^x sinx+e^x cosx−∫e^x cosx=I 2I=e^x (sinx+cosx) I=(e^x /2)(sinx+cosx)+C

$$\left.\mathrm{1}\right)\int\mathrm{5}^{\left({x}^{\mathrm{2}} +\mathrm{6}\right)} \left({x}+\mathrm{3}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{5}^{{u}} {du}\:\:\:\:\:\:\:\:\left\{{u}={x}^{\mathrm{2}} +\mathrm{6}{x}\:\:\:\frac{{du}}{{dx}}=\mathrm{2}{x}+\mathrm{6}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{5}^{{u}} }{{log}\mathrm{5}}+{C}=\frac{\mathrm{1}}{\mathrm{2}{log}\mathrm{5}}\mathrm{5}^{{x}^{\mathrm{2}} +\mathrm{6}{x}} +{C} \\ $$$$\left.\mathrm{2}\right)\int{e}^{{x}} {cosxdx}={I} \\ $$$$={e}^{{x}} {sinx}−\int{e}^{{x}} {sinx} \\ $$$$={e}^{{x}} {sinx}+{e}^{{x}} {cosx}−\int{e}^{{x}} {cosx}={I} \\ $$$$\mathrm{2}{I}={e}^{{x}} \left({sinx}+{cosx}\right) \\ $$$${I}=\frac{{e}^{{x}} }{\mathrm{2}}\left({sinx}+{cosx}\right)+{C} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 26/Jul/20

b)lim_(x→0) ((tanx)/x)=((sinx)/x).(1/(cosx))=(x/x).1=1 as sinx→x

$$\left.{b}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tanx}}{{x}}=\frac{{sinx}}{{x}}.\frac{\mathrm{1}}{{cosx}}=\frac{{x}}{{x}}.\mathrm{1}=\mathrm{1}\:\:\:\:{as}\:{sinx}\rightarrow{x} \\ $$

Answered by Dwaipayan Shikari last updated on 26/Jul/20

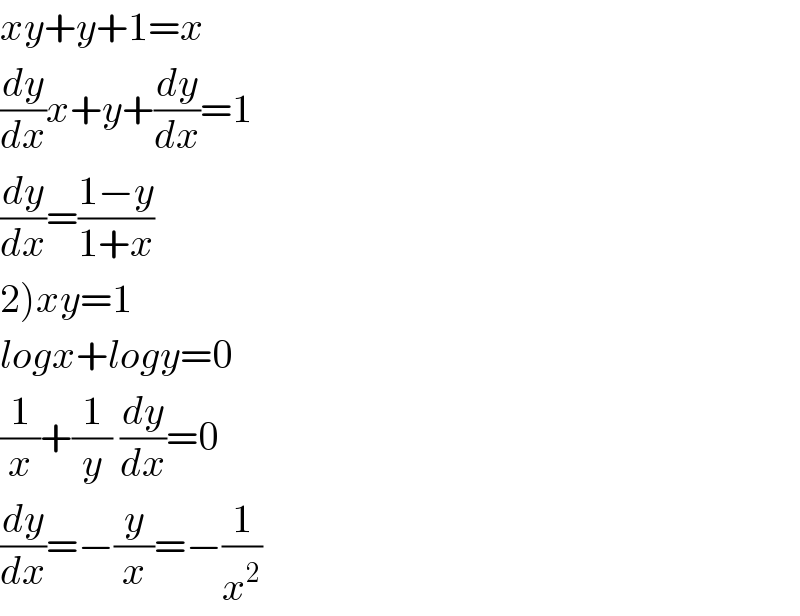
xy+y+1=x (dy/dx)x+y+(dy/dx)=1 (dy/dx)=((1−y)/(1+x)) 2)xy=1 logx+logy=0 (1/x)+(1/y) (dy/dx)=0 (dy/dx)=−(y/x)=−(1/x^2 )

$${xy}+{y}+\mathrm{1}={x} \\ $$$$\frac{{dy}}{{dx}}{x}+{y}+\frac{{dy}}{{dx}}=\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}−{y}}{\mathrm{1}+{x}} \\ $$$$\left.\mathrm{2}\right){xy}=\mathrm{1} \\ $$$${logx}+{logy}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{y}}{{x}}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$

Answered by Dwaipayan Shikari last updated on 26/Jul/20

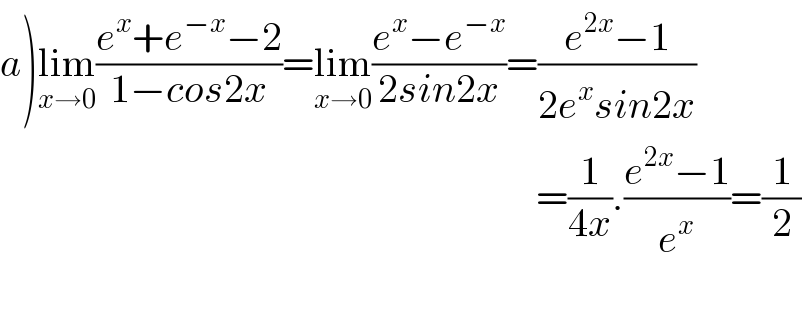
a)lim_(x→0) ((e^x +e^(−x) −2)/(1−cos2x))=lim_(x→0) ((e^x −e^(−x) )/(2sin2x))=((e^(2x) −1)/(2e^x sin2x)) =(1/(4x)).((e^(2x) −1)/e^x )=(1/2)

$$\left.{a}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} +{e}^{−{x}} −\mathrm{2}}{\mathrm{1}−{cos}\mathrm{2}{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}{sin}\mathrm{2}{x}}=\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{2}{e}^{{x}} {sin}\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}{x}}.\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{{x}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Answered by Dwaipayan Shikari last updated on 26/Jul/20

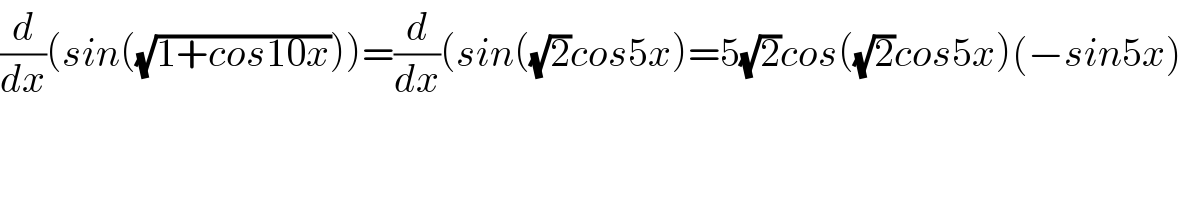
(d/dx)(sin((√(1+cos10x))))=(d/dx)(sin((√2)cos5x)=5(√2)cos((√2)cos5x)(−sin5x)

$$\frac{{d}}{{dx}}\left({sin}\left(\sqrt{\mathrm{1}+{cos}\mathrm{10}{x}}\right)\right)=\frac{{d}}{{dx}}\left({sin}\left(\sqrt{\mathrm{2}}{cos}\mathrm{5}{x}\right)=\mathrm{5}\sqrt{\mathrm{2}}{cos}\left(\sqrt{\mathrm{2}}{cos}\mathrm{5}{x}\right)\left(−{sin}\mathrm{5}{x}\right)\right. \\ $$

Answered by mathmax by abdo last updated on 26/Jul/20

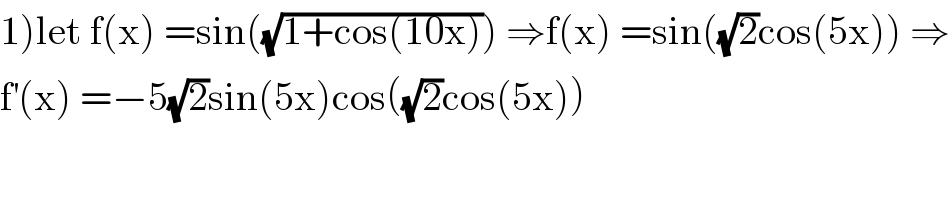
1)let f(x) =sin((√(1+cos(10x)))) ⇒f(x) =sin((√2)cos(5x)) ⇒ f^′ (x) =−5(√2)sin(5x)cos((√2)cos(5x))

$$\left.\mathrm{1}\right)\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{sin}\left(\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{sin}\left(\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{5x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\mathrm{5}\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{5x}\right)\mathrm{cos}\left(\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{5x}\right)\right) \\ $$

Answered by mathmax by abdo last updated on 26/Jul/20

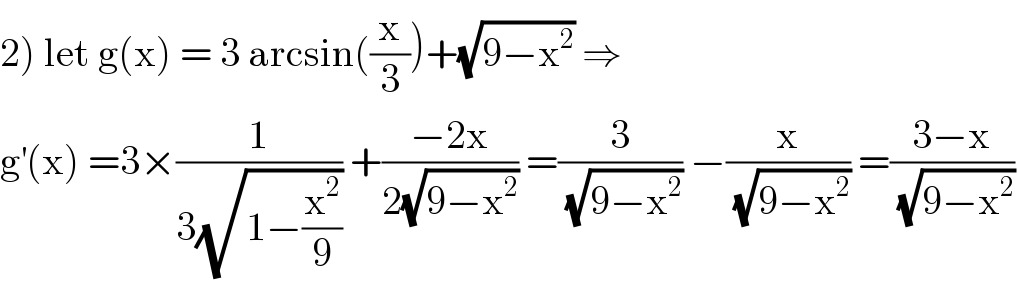
2) let g(x) = 3 arcsin((x/3))+(√(9−x^2 )) ⇒ g^′ (x) =3×(1/(3(√(1−(x^2 /9))))) +((−2x)/(2(√(9−x^2 )))) =(3/(√(9−x^2 ))) −(x/(√(9−x^2 ))) =((3−x)/(√(9−x^2 )))

$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\:\mathrm{3}\:\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)+\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{x}\right)\:=\mathrm{3}×\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}}}\:+\frac{−\mathrm{2x}}{\mathrm{2}\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }}\:=\frac{\mathrm{3}}{\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }}\:−\frac{\mathrm{x}}{\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }}\:=\frac{\mathrm{3}−\mathrm{x}}{\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }} \\ $$

Answered by mathmax by abdo last updated on 26/Jul/20

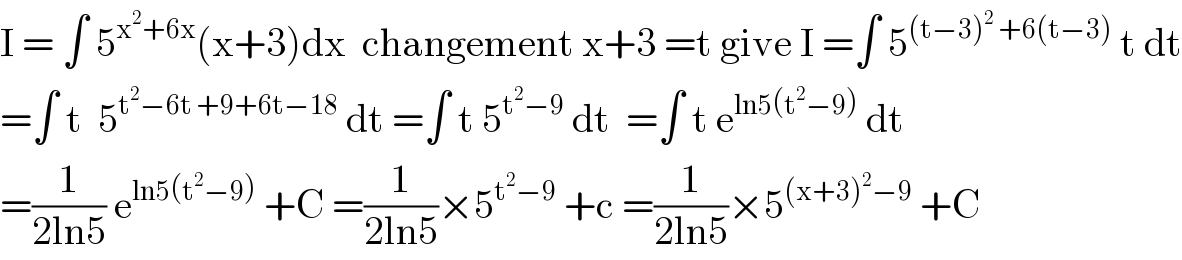
I = ∫ 5^(x^2 +6x) (x+3)dx changement x+3 =t give I =∫ 5^((t−3)^2 +6(t−3)) t dt =∫ t 5^(t^2 −6t +9+6t−18) dt =∫ t 5^(t^2 −9) dt =∫ t e^(ln5(t^2 −9)) dt =(1/(2ln5)) e^(ln5(t^2 −9)) +C =(1/(2ln5))×5^(t^2 −9) +c =(1/(2ln5))×5^((x+3)^2 −9) +C

$$\mathrm{I}\:=\:\int\:\mathrm{5}^{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}} \left(\mathrm{x}+\mathrm{3}\right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}+\mathrm{3}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{I}\:=\int\:\mathrm{5}^{\left(\mathrm{t}−\mathrm{3}\right)^{\mathrm{2}} \:+\mathrm{6}\left(\mathrm{t}−\mathrm{3}\right)} \:\mathrm{t}\:\mathrm{dt} \\ $$$$=\int\:\mathrm{t}\:\:\mathrm{5}^{\mathrm{t}^{\mathrm{2}} −\mathrm{6t}\:+\mathrm{9}+\mathrm{6t}−\mathrm{18}} \:\mathrm{dt}\:=\int\:\mathrm{t}\:\mathrm{5}^{\mathrm{t}^{\mathrm{2}} −\mathrm{9}} \:\mathrm{dt}\:\:=\int\:\mathrm{t}\:\mathrm{e}^{\mathrm{ln5}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{9}\right)} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2ln5}}\:\mathrm{e}^{\mathrm{ln5}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{9}\right)} \:+\mathrm{C}\:=\frac{\mathrm{1}}{\mathrm{2ln5}}×\mathrm{5}^{\mathrm{t}^{\mathrm{2}} −\mathrm{9}} \:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{2ln5}}×\mathrm{5}^{\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}} \:+\mathrm{C} \\ $$

Answered by 1549442205PVT last updated on 26/Jul/20

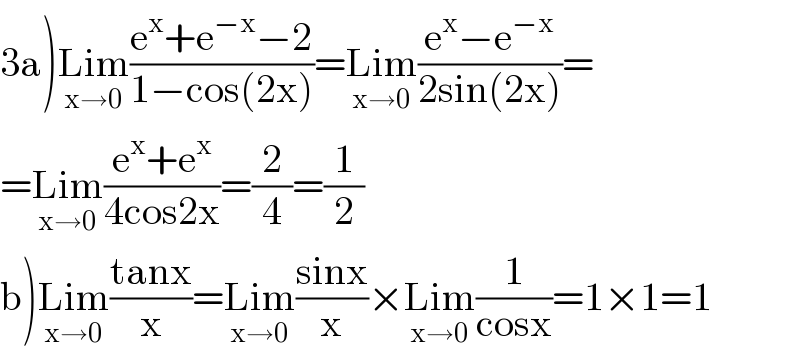
3a)Lim_(x→0) ((e^x +e^(−x) −2)/(1−cos(2x)))=Lim_(x→0) ((e^x −e^(−x) )/(2sin(2x)))= =Lim_(x→0) ((e^x +e^x )/(4cos2x))=(2/4)=(1/2) b)Lim_(x→0) ((tanx)/x)=Lim_(x→0) ((sinx)/x)×Lim_(x→0) (1/(cosx))=1×1=1

$$\left.\mathrm{3a}\right)\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} −\mathrm{2}}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{2sin}\left(\mathrm{2x}\right)}= \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{\mathrm{x}} }{\mathrm{4cos2x}}=\frac{\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{b}\right)\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{tanx}}{\mathrm{x}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{sinx}}{\mathrm{x}}×\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{1}}{\mathrm{cosx}}=\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$

Answered by 1549442205PVT last updated on 26/Jul/20

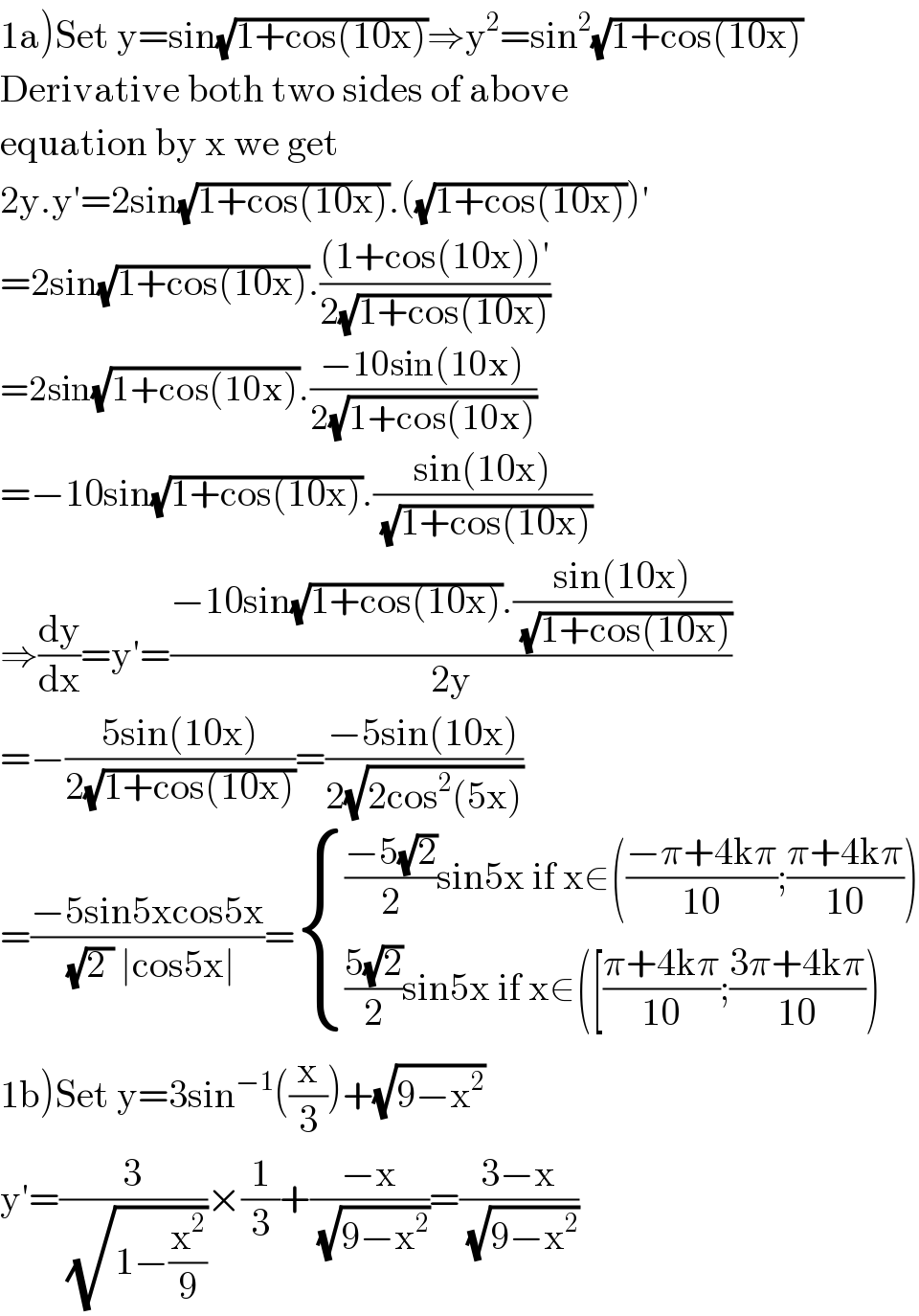
1a)Set y=sin(√(1+cos(10x)))⇒y^2 =sin^2 (√(1+cos(10x))) Derivative both two sides of above equation by x we get 2y.y′=2sin(√(1+cos(10x))).((√(1+cos(10x))))′ =2sin(√(1+cos(10x))).(((1+cos(10x))′)/(2(√(1+cos(10x))))) =2sin(√(1+cos(10x))).((−10sin(10x))/(2(√(1+cos(10x))))) =−10sin(√(1+cos(10x))).((sin(10x))/(√(1+cos(10x)))) ⇒(dy/dx)=y′=((−10sin(√(1+cos(10x))).((sin(10x))/(√(1+cos(10x)))))/(2y)) =−((5sin(10x))/(2(√(1+cos(10x)))))=((−5sin(10x))/(2(√(2cos^2 (5x))))) =((−5sin5xcos5x)/((√(2 )) ∣cos5x∣))= { ((((−5(√2))/2)sin5x if x∈(((−π+4kπ)/(10));((π+4kπ)/(10))))),((((5(√2))/2)sin5x if x∈([((π+4kπ)/(10));((3π+4kπ)/(10))))) :} 1b)Set y=3sin^(−1) ((x/3))+(√(9−x^2 )) y′=(3/(√(1−(x^2 /9))))×(1/3)+((−x)/(√(9−x^2 )))=((3−x)/(√(9−x^2 )))

$$\left.\mathrm{1a}\right)\mathrm{Set}\:\mathrm{y}=\mathrm{sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{sin}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)} \\ $$$$\mathrm{Derivative}\:\mathrm{both}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{above} \\ $$$$\mathrm{equation}\:\mathrm{by}\:\mathrm{x}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{2y}.\mathrm{y}'=\mathrm{2sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}.\left(\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}\right)' \\ $$$$=\mathrm{2sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}.\frac{\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)\right)'}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}} \\ $$$$=\mathrm{2sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}.\frac{−\mathrm{10sin}\left(\mathrm{10x}\right)}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}} \\ $$$$=−\mathrm{10sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}.\frac{\mathrm{sin}\left(\mathrm{10x}\right)}{\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}} \\ $$$$\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{y}'=\frac{−\mathrm{10sin}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}.\frac{\mathrm{sin}\left(\mathrm{10x}\right)}{\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}}}{\mathrm{2y}} \\ $$$$=−\frac{\mathrm{5sin}\left(\mathrm{10x}\right)}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}}=\frac{−\mathrm{5sin}\left(\mathrm{10x}\right)}{\mathrm{2}\sqrt{\mathrm{2cos}^{\mathrm{2}} \left(\mathrm{5x}\right)}} \\ $$$$=\frac{−\mathrm{5sin5xcos5x}}{\sqrt{\mathrm{2}\:}\:\mid\mathrm{cos5x}\mid}=\begin{cases}{\frac{−\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{sin5x}\:\mathrm{if}\:\mathrm{x}\in\left(\frac{−\pi+\mathrm{4k}\pi}{\mathrm{10}};\frac{\pi+\mathrm{4k}\pi}{\mathrm{10}}\right)}\\{\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{sin5x}\:\mathrm{if}\:\mathrm{x}\in\left(\left[\frac{\pi+\mathrm{4k}\pi}{\mathrm{10}};\frac{\mathrm{3}\pi+\mathrm{4k}\pi}{\mathrm{10}}\right)\right.}\end{cases} \\ $$$$\left.\mathrm{1b}\right)\mathrm{Set}\:\mathrm{y}=\mathrm{3sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{3}}\right)+\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }\: \\ $$$$\mathrm{y}'=\frac{\mathrm{3}}{\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}}}×\frac{\mathrm{1}}{\mathrm{3}}+\frac{−\mathrm{x}}{\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }}=\frac{\mathrm{3}−\mathrm{x}}{\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }} \\ $$

Answered by 1549442205PVT last updated on 26/Jul/20

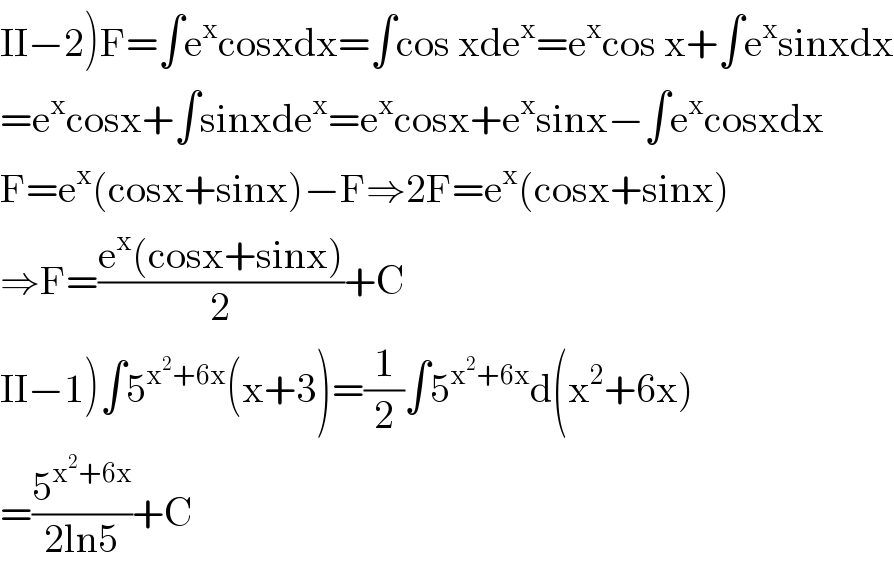
II−2)F=∫e^x cosxdx=∫cos xde^x =e^x cos x+∫e^x sinxdx =e^x cosx+∫sinxde^x =e^x cosx+e^x sinx−∫e^x cosxdx F=e^x (cosx+sinx)−F⇒2F=e^x (cosx+sinx) ⇒F=((e^x (cosx+sinx))/2)+C II−1)∫5^(x^2 +6x) (x+3)=(1/2)∫5^(x^2 +6x) d(x^2 +6x) =(5^(x^2 +6x) /(2ln5))+C

$$\left.\mathrm{II}−\mathrm{2}\right)\mathrm{F}=\int\mathrm{e}^{\mathrm{x}} \mathrm{cosxdx}=\int\mathrm{cos}\:\mathrm{xde}^{\mathrm{x}} =\mathrm{e}^{\mathrm{x}} \mathrm{cos}\:\mathrm{x}+\int\mathrm{e}^{\mathrm{x}} \mathrm{sinxdx} \\ $$$$=\mathrm{e}^{\mathrm{x}} \mathrm{cosx}+\int\mathrm{sinxde}^{\mathrm{x}} =\mathrm{e}^{\mathrm{x}} \mathrm{cosx}+\mathrm{e}^{\mathrm{x}} \mathrm{sinx}−\int\mathrm{e}^{\mathrm{x}} \mathrm{cosxdx} \\ $$$$\mathrm{F}=\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{sinx}\right)−\mathrm{F}\Rightarrow\mathrm{2F}=\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{sinx}\right) \\ $$$$\Rightarrow\mathrm{F}=\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{cosx}+\mathrm{sinx}\right)}{\mathrm{2}}+\mathrm{C} \\ $$$$\left.\mathrm{II}−\mathrm{1}\right)\int\mathrm{5}^{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}} \left(\mathrm{x}+\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{5}^{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}} \mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}\right) \\ $$$$=\frac{\mathrm{5}^{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}} }{\mathrm{2ln5}}+\mathrm{C} \\ $$

Answered by 1549442205PVT last updated on 26/Jul/20

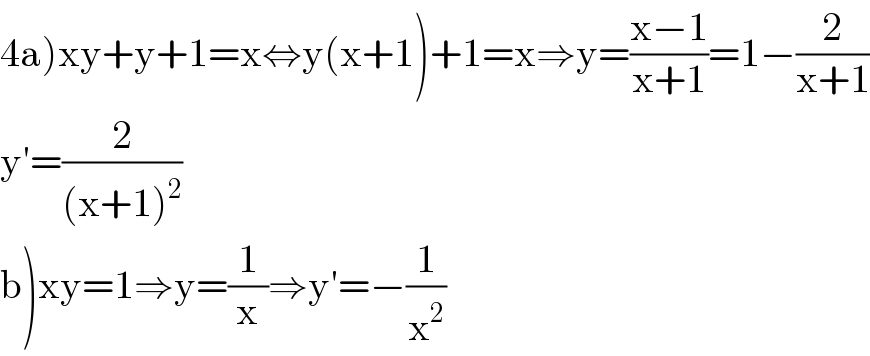
4a)xy+y+1=x⇔y(x+1)+1=x⇒y=((x−1)/(x+1))=1−(2/(x+1)) y′=(2/((x+1)^2 )) b)xy=1⇒y=(1/x)⇒y′=−(1/x^2 )

$$\left.\mathrm{4a}\right)\mathrm{xy}+\mathrm{y}+\mathrm{1}=\mathrm{x}\Leftrightarrow\mathrm{y}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{1}=\mathrm{x}\Rightarrow\mathrm{y}=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{y}'=\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{b}\right)\mathrm{xy}=\mathrm{1}\Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{x}}\Rightarrow\mathrm{y}'=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com