Question Number 105163 by bemath last updated on 26/Jul/20

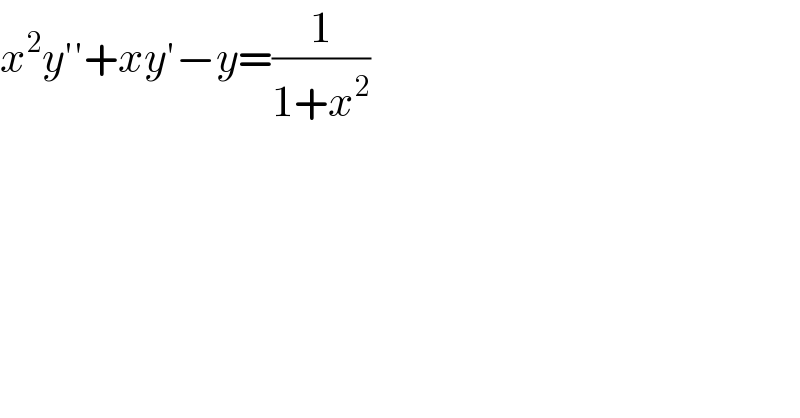
x^2 y′′+xy′−y=(1/(1+x^2 ))

Answered by bramlex last updated on 27/Jul/20

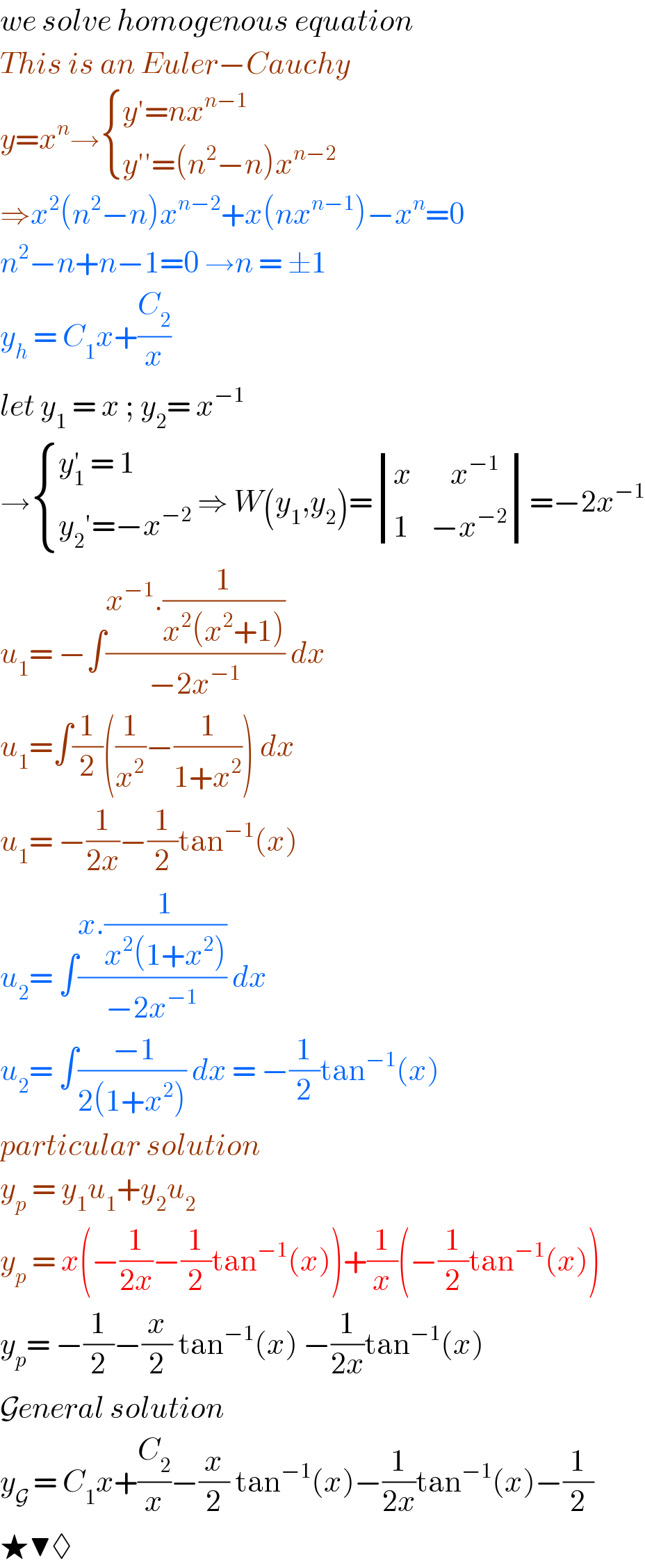
we solve homogenous equation This is an Euler−Cauchy y=x^n → { ((y′=nx^(n−1) )),((y′′=(n^2 −n)x^(n−2) )) :} ⇒x^2 (n^2 −n)x^(n−2) +x(nx^(n−1) )−x^n =0 n^2 −n+n−1=0 →n = ±1 y_h = C_1 x+(C_2 /x) let y_1 = x ; y_2 = x^(−1) → { ((y_1 ^′ = 1)),((y_2 ′=−x^(−2) )) :} ⇒ W(y_1 ,y_2 )= determinant (((x x^(−1) )),((1 −x^(−2) )))=−2x^(−1) u_1 = −∫((x^(−1) .(1/(x^2 (x^2 +1))))/(−2x^(−1) )) dx u_1 =∫(1/2)((1/x^2 )−(1/(1+x^2 ))) dx u_1 = −(1/(2x))−(1/2)tan^(−1) (x) u_2 = ∫((x.(1/(x^2 (1+x^2 ))))/(−2x^(−1) )) dx u_2 = ∫(( −1)/(2(1+x^2 ))) dx = −(1/2)tan^(−1) (x) particular solution y_p = y_1 u_1 +y_2 u_2 y_p = x(−(1/(2x))−(1/2)tan^(−1) (x))+(1/x)(−(1/2)tan^(−1) (x)) y_p = −(1/2)−(x/2) tan^(−1) (x) −(1/(2x))tan^(−1) (x) General solution y_G = C_1 x+(C_2 /x)−(x/2) tan^(−1) (x)−(1/(2x))tan^(−1) (x)−(1/2) ★▼◊

Answered by OlafThorendsen last updated on 26/Jul/20

(x^2 y′′+2xy′)−(xy′+y) = (1/(1+x^2 )) (x^2 y′)′−(xy)′ = (1/(1+x^2 )) x^2 y′−xy = arctanx+C_1 ((xy′−y)/x^2 ) = (1/x^3 )arctanx+(C_1 /x^3 ) (d/dx)((y/x)) = (1/x^3 )arctanx+(C_1 /x^3 ) (y/x) = −(1/(2x^2 ))arctanx+∫(dx/(2x^2 (1+x^2 )))+(C_2 /x^2 )+C_3 (1/(x^2 (1+x^2 ))) = (1/x^2 )−(1/(1+x^2 )) (y/x) = −(1/(2x^2 ))arctanx−(1/(2x))−(1/2)arctanx+(C_2 /x^2 )+C_3 y = −(1/(2x))arctanx−(1/2)xarctanx+(C_2 /x)+C_3 x−(1/2)

Answered by mathmax by abdo last updated on 26/Jul/20

x^2 y^(′′) +xy^′ −y =(1/(1+x^2 )) h→x^2 y^((2)) +xy^((1)) −y =0 let y =x^m ⇒y^′ =mx^(m−1) and y^((2)) =m(m−1)x^(m−2) e⇒m(m−1)x^m +mx^m −x^m =0 ⇒(m^2 −m+m−1)x^m =0 ⇒ m^2 −1=0 ⇒m =+^− 1 ⇒y =αx +(β/x) =αu_1 +β u_2 W(u_1 ,u_2 ) = determinant (((x (1/x))),((1 −(1/x^2 ))))=−(1/x)−(1/x) =−(2/x) ≠0 W_1 = determinant (((o (1/x))),(((1/(1+x^2 )) −(1/x^2 ))))=−(1/(x(1+x^2 ))) W_2 = determinant (((x 0)),((1 (1/(1+x^2 )))))=(x/(1+x^2 )) v_1 =∫ (w_1 /w)dx =−∫ (1/(x(1+x^2 )))×(((−x)/2))dx =(1/2) ∫ (dx/((1+x^2 )))=(1/2)arctanx =∫ (w_2 /w)dx =∫ (x/(1+x^2 ))×(−(x/2))dx =−(1/2)∫ (x^2 /(1+x^2 ))dx =−(1/2)∫((1+x^2 −1)/(1+x^2 ))dx =−(x/2) +(1/2)arctanx ⇒ y_p =u_1 v_1 +u_2 v_2 =(x/2)arctanx+(1/x)(−(x/2) +(1/2) arctanx) =(x/2) arctanx−(1/2) +(1/(2x)) arctanx =(1/2)(x+(1/x))arctanx−(1/2) the general solution is y =αx +βx^(−1) +(1/2)(x+(1/x))arctanx −(1/2)