Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 10521 by ajfour last updated on 16/Feb/17

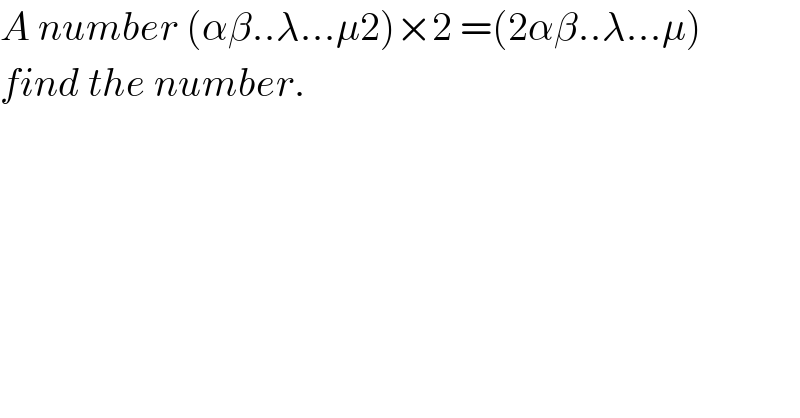
A number (αβ..λ...μ2)×2 =(2αβ..λ...μ) find the number.

$${A}\:{number}\:\left(\alpha\beta..\lambda...\mu\mathrm{2}\right)×\mathrm{2}\:=\left(\mathrm{2}\alpha\beta..\lambda...\mu\right) \\ $$$${find}\:{the}\:{number}. \\ $$$$ \\ $$

Answered by mrW1 last updated on 17/Feb/17

(Part I) let x=(αβ..λ...μ)=a number with n−1 digits let y=(αβ..λ...μ2)=a number with n digits let z=(2αβ..λ...μ)=a number with n digits y=x×10+2=10x+2 z=2×10...0+x=2×10^(n−1) +x (αβ..λ...μ2)×2 =(2αβ..λ...μ) ⇔y×2=z (10x+2)×2=2×10^(n−1) +x 19x=2×10^(n−1) −4=2(10^(n−1) −2) x=((2(10^(n−1) −2))/(19)) the first suitable number is n=18 and x=((2(10^(17) −2))/(19))=10526315789473684 y=105263157894736842 (105263157894736842)×2=(210526315789473684) the second suitable number is n=36 and x=((2(10^(35) −2))/(19))=10526315789473684210526315789473684 y=105263157894736842105263157894736842 (105263157894736842105263157894736842)×2=(210526315789473684210526315789473684) the third suitable number is n=54 and x=((2(10^(53) −2))/(19))=10526315789473684210526315789473684210526315789474684 y=105263157894736842105263157894736842105263157894736842 (105263157894736842105263157894736842105263157894736842)×2=(210526315789473684210526315789473684210526315789473684) the general solution is n=18i with i=1,2,... and the number is y=105263157894736842105263157894736842105263157894736842105263157894736842......

$$\left({Part}\:{I}\right) \\ $$$${let}\:{x}=\left(\alpha\beta..\lambda...\mu\right)={a}\:{number}\:{with}\:{n}−\mathrm{1}\:{digits} \\ $$$${let}\:{y}=\left(\alpha\beta..\lambda...\mu\mathrm{2}\right)={a}\:{number}\:{with}\:{n}\:{digits} \\ $$$${let}\:{z}=\left(\mathrm{2}\alpha\beta..\lambda...\mu\right)={a}\:{number}\:{with}\:{n}\:{digits} \\ $$$${y}={x}×\mathrm{10}+\mathrm{2}=\mathrm{10}{x}+\mathrm{2} \\ $$$${z}=\mathrm{2}×\mathrm{10}...\mathrm{0}+{x}=\mathrm{2}×\mathrm{10}^{{n}−\mathrm{1}} +{x} \\ $$$$ \\ $$$$\left(\alpha\beta..\lambda...\mu\mathrm{2}\right)×\mathrm{2}\:=\left(\mathrm{2}\alpha\beta..\lambda...\mu\right) \\ $$$$\Leftrightarrow{y}×\mathrm{2}={z} \\ $$$$\left(\mathrm{10}{x}+\mathrm{2}\right)×\mathrm{2}=\mathrm{2}×\mathrm{10}^{{n}−\mathrm{1}} +{x} \\ $$$$\mathrm{19}{x}=\mathrm{2}×\mathrm{10}^{{n}−\mathrm{1}} −\mathrm{4}=\mathrm{2}\left(\mathrm{10}^{{n}−\mathrm{1}} −\mathrm{2}\right) \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{10}^{{n}−\mathrm{1}} −\mathrm{2}\right)}{\mathrm{19}} \\ $$$$ \\ $$$${the}\:{first}\:{suitable}\:{number}\:{is}\:{n}=\mathrm{18}\:{and} \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{10}^{\mathrm{17}} −\mathrm{2}\right)}{\mathrm{19}}=\mathrm{10526315789473684} \\ $$$${y}=\mathrm{105263157894736842} \\ $$$$\left(\mathrm{105263157894736842}\right)×\mathrm{2}=\left(\mathrm{210526315789473684}\right) \\ $$$$ \\ $$$${the}\:{second}\:{suitable}\:{number}\:{is}\:{n}=\mathrm{36}\:{and} \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{10}^{\mathrm{35}} −\mathrm{2}\right)}{\mathrm{19}}=\mathrm{10526315789473684210526315789473684} \\ $$$${y}=\mathrm{105263157894736842105263157894736842} \\ $$$$\left(\mathrm{105263157894736842105263157894736842}\right)×\mathrm{2}=\left(\mathrm{210526315789473684210526315789473684}\right) \\ $$$$ \\ $$$${the}\:{third}\:{suitable}\:{number}\:{is}\:{n}=\mathrm{54}\:{and} \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{10}^{\mathrm{53}} −\mathrm{2}\right)}{\mathrm{19}}=\mathrm{10526315789473684210526315789473684210526315789474684} \\ $$$${y}=\mathrm{105263157894736842105263157894736842105263157894736842} \\ $$$$\left(\mathrm{105263157894736842105263157894736842105263157894736842}\right)×\mathrm{2}=\left(\mathrm{210526315789473684210526315789473684210526315789473684}\right) \\ $$$$ \\ $$$${the}\:{general}\:{solution}\:{is}\:{n}=\mathrm{18}{i}\:{with}\:{i}=\mathrm{1},\mathrm{2},... \\ $$$${and}\:{the}\:{number}\:{is} \\ $$$${y}=\mathrm{105263157894736842105263157894736842105263157894736842105263157894736842}...... \\ $$

Commented by ajfour last updated on 16/Feb/17

great explanation, i cud arrive at the answer but ur explanation is elaborate. but wait, it should end with.... 736842.typing error probably.

$${great}\:{explanation},\:{i}\:{cud}\:{arrive}\:{at}\:{the}\:{answer}\:{but}\:{ur}\:{explanation}\:{is}\:{elaborate}.\:{but}\:{wait},\:{it}\:{should}\:{end}\:{with}....\:\mathrm{736842}.{typing}\:{error}\:{probably}. \\ $$

Commented by mrW1 last updated on 16/Feb/17

you are right. i had a typing error. now it′s fixed. thank you for pointing out that.

$${you}\:{are}\:{right}.\:{i}\:{had}\:{a}\:{typing}\:{error}.\: \\ $$$${now}\:{it}'{s}\:{fixed}.\:{thank}\:{you}\:{for}\:{pointing}\:{out}\:{that}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com