
Question Number 105230 by mathmax by abdo last updated on 27/Jul/20
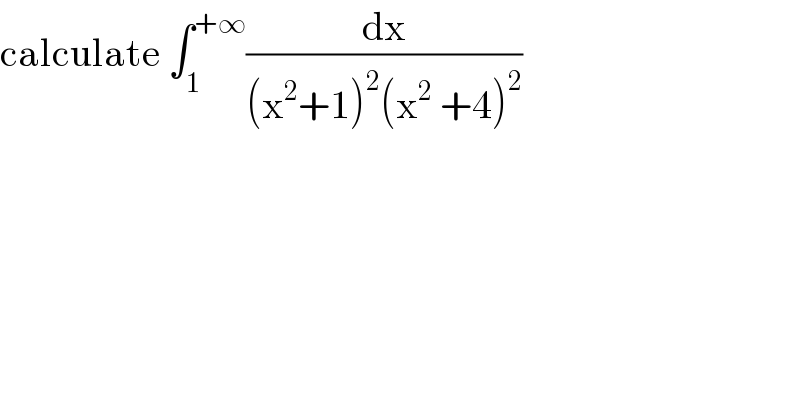
$$\mathrm{calculate}\:\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} } \\ $$
Answered by 1549442205PVT last updated on 27/Jul/20
![F=∫[(1/4)((1/x^2 )−(1/(x^2 +4)))]^2 dx 16F=∫[(1/x^4 )+(1/((x^2 +4)^2 ))−(2/(x^2 (x^2 +4)))]dx =∫(dx/x^4 )+∫((1/(2(x^2 +4)))−(1/(2x^2 )))dx+∫ (dx/((x^2 +4)^2 )) =−(1/(3x^3 ))+(1/(2x))+(1/2)×(1/2)tan^(−1) ((x/2))+I_2 =−(1/(3x^3 ))+(1/(2x))+(1/4)tan^(−1) ((x/2))+(1/(2.4)).(x/((x^2 +4)))+(1/4).(1/2).(1/2)tan^(−1) ((x/2)) =−(1/(3x^3 ))+(1/(2x))+(x/(8(x^2 +4)))+(5/(16))tan^(−1) ((x/2)) F=(1/(16)){−(1/(3x^3 ))+(1/(2x))+(x/(8(x^2 +4)))+(5/(16))tan^(−1) ((x/2))} I= ∫_1 ^(+∞) (dx/((x^2 +1)^2 (x^2 +4)^2 ))=F(+∞)−F(1) =(1/(16)){(5/(16))×(𝛑/2)−[((23)/(120))+(5/(16))tan^(−1) ((1/2))]}](Q105339.png)
$$\mathrm{F}=\int\left[\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}\right)\right]^{\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{16F}=\int\left[\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}\right]\mathrm{dx} \\ $$$$=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} }+\int\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}−\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\right)\mathrm{dx}+\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{I}_{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}}.\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{x}}{\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$$$\mathrm{F}=\frac{\mathrm{1}}{\mathrm{16}}\left\{−\frac{\mathrm{1}}{\mathrm{3x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{x}}{\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right\} \\ $$$$\mathrm{I}=\:\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{F}\left(+\infty\right)−\mathrm{F}\left(\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left\{\frac{\mathrm{5}}{\mathrm{16}}×\frac{\boldsymbol{\pi}}{\mathrm{2}}−\left[\frac{\mathrm{23}}{\mathrm{120}}+\frac{\mathrm{5}}{\mathrm{16}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right]\right\} \\ $$
Commented by abdomsup last updated on 28/Jul/20

$${thank}\:{you}\:{sir} \\ $$
Commented by 1549442205PVT last updated on 28/Jul/20

$$\mathrm{Thank},\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
Answered by mathmax by abdo last updated on 29/Jul/20
![I =∫_1 ^(+∞) (dx/((x^2 +1)^2 (x^2 +4)^2 )) we have F(x)= (1/((x^2 +1)^2 (x^2 +4)^2 )) =(1/9)((1/(x^2 +1))−(1/(x^2 +4)))^2 =(1/9){ (1/((x^2 +1)^2 )) −(2/((x^2 +1)(x^2 +4))) +(1/((x^2 +4)^2 ))} ⇒ 9F(x) =(1/((x^2 +1)^2 )) −(2/3)((1/(x^2 +1))−(1/(x^2 +4)))+(1/((x^2 +4)^2 )) =(1/((x^2 +1)^2 ))−(2/(3(x^2 +1))) +(2/(3(x^2 +4))) +(1/((x^2 +4)^2 )) ⇒ 9 ∫_1 ^∞ F(x) =∫_1 ^∞ (dx/((1+x^2 )^2 ))−(2/3)∫_1 ^∞ (dx/(1+x^2 )) +(2/3)∫_1 ^∞ (dx/(x^2 +4)) +∫_1 ^∞ (dx/((x^2 +4)^2 )) we have ∫_1 ^∞ (dx/((1+x^2 )^2 )) =_(x=tant) ∫_(π/4) ^(π/2) (((1+tan^2 t))/((1+tan^2 t)^2 ))dt =∫_(π/4) ^(π/2) cos^2 t dt =(1/2)∫_(π/4) ^(π/2) (1+cos(2t))dt =(π/8) +(1/4)[sin(2t)]_(π/4) ^(π/2) =(π/8) −(1/4) and ∫_1 ^∞ (dx/(1+x^2 )) =[arctanx]_1 ^∞ =(π/2)−(π/4) =(π/4) ∫_1 ^∞ (dx/(x^2 +4)) =_(x=2t) ∫_(1/2) ^∞ ((2dt)/(4(1+t^2 ))) =(1/2)((π/2)−arctan((1/2))) =(π/4) −(1/2)((π/2)−arctan2) =((arctan2)/2) ∫_1 ^∞ (dx/((x^2 +4)^2 )) =_(x=2t) ∫_(1/2) ^∞ ((2dt)/(16(t^2 +1)^2 )) =(1/8) ∫_(1/2) ^∞ (dt/((1+t^2 )^2 )) =_(t=tanu) (1/8) ∫_(arctan((1/2))) ^(π/2) ((1+tan^2 u)/((1+tan^2 u)^2 ))du =(1/8)∫_(arctan((1/2))) ^(π/2) ((1+cos(2u))/2) du =(1/(16))∫_(arctan((1/2))) ^(π/2) (1+cos(2u)du =(1/(16))((π/2)−arctan((1/2)))+(1/(32))[sin(2u)]_(...) ^(...) =((arctan2)/(16)) +(1/(32))(−sin(2arctan((1/2))) so the value of I is known](Q105445.png)
$$\mathrm{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{F}\left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left\{\:\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\:+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$$\mathrm{9F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\right)+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\:+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{9}\:\int_{\mathrm{1}} ^{\infty} \:\mathrm{F}\left(\mathrm{x}\right)\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{\mathrm{x}=\mathrm{tant}} \:\:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt}\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\:\mathrm{and}\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\left[\mathrm{arctanx}\right]_{\mathrm{1}} ^{\infty} \:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:=_{\mathrm{x}=\mathrm{2t}} \:\:\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\infty} \:\frac{\mathrm{2dt}}{\mathrm{4}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan2}\right)\:=\frac{\mathrm{arctan2}}{\mathrm{2}} \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\:=_{\mathrm{x}=\mathrm{2t}} \:\:\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\infty} \:\frac{\mathrm{2dt}}{\mathrm{16}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=_{\mathrm{t}=\mathrm{tanu}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{u}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2u}\right)}{\mathrm{2}}\:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2u}\right)\mathrm{du}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\frac{\mathrm{1}}{\mathrm{32}}\left[\mathrm{sin}\left(\mathrm{2u}\right)\right]_{...} ^{...} \\ $$$$=\frac{\mathrm{arctan2}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{32}}\left(−\mathrm{sin}\left(\mathrm{2arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{I}\:\mathrm{is}\:\mathrm{known}\right. \\ $$
