
Question Number 106779 by bobhans last updated on 07/Aug/20
$$\:\:\:\:\:\:\:\:\:^{\succ\mathrm{bobhans}\prec} \\ $$$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{find}\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{closest}\:\mathrm{to}\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{0},\mathrm{18}\right)\:? \\ $$
Answered by john santu last updated on 07/Aug/20

$$\:\:\:\:\:\:\:^{@\mathrm{JS}@} \\ $$$$\mathrm{let}\:\left(\sqrt{\mathrm{x}}\:,\mathrm{x}\right)\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{closest}\:\mathrm{to}\:\mathrm{point}\:\left(\mathrm{0},\mathrm{18}\right) \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\mathrm{d}\:=\:\sqrt{\left(\sqrt{\mathrm{x}}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{x}−\mathrm{18}\right)^{\mathrm{2}} } \\ $$$$\mathrm{d}\:=\:\sqrt{\mathrm{x}+\mathrm{x}^{\mathrm{2}} −\mathrm{36x}+\mathrm{324}}\: \\ $$$$\mathrm{d}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{35x}+\mathrm{324}} \\ $$$$\mathrm{put}\:\mathrm{d}'\:=\:\mathrm{0}\:\Rightarrow\mathrm{d}'=\frac{\mathrm{2x}−\mathrm{35}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{35x}+\mathrm{324}}}=\mathrm{0} \\ $$$$\rightarrow\mathrm{so}\:\mathrm{the}\:\mathrm{coordinates}\:\mathrm{point}\:\mathrm{we} \\ $$$$\mathrm{search}\:\mathrm{is}\:\left(\pm\sqrt{\frac{\mathrm{35}}{\mathrm{2}}}\:,\:\frac{\mathrm{35}}{\mathrm{2}}\right)\:.\: \\ $$
Answered by bobhans last updated on 07/Aug/20

$$\:\:\:\:\:\:\:^{\succ\mathrm{bobhans}\prec} \\ $$$$\mathrm{find}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} \:\mathrm{at}\:\left(\mathrm{x}_{\mathrm{o}} ,\mathrm{y}_{\mathrm{o}} \right)\:\mathrm{is}\:\mathrm{y}=\mathrm{2x}_{\mathrm{o}} \left(\mathrm{x}−\mathrm{x}_{\mathrm{o}} \right)+\mathrm{y}_{\mathrm{o}} \\ $$$$\mathrm{find}\:\mathrm{normal}\:\mathrm{to}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} \:\mathrm{at}\:\left(\mathrm{x}_{\mathrm{o}} ,\mathrm{y}_{\mathrm{o}} \right)\:\mathrm{is}\: \\ $$$$\mathrm{y}=−\frac{\mathrm{1}}{\mathrm{2x}_{\mathrm{o}} }\left(\mathrm{x}−\mathrm{x}_{\mathrm{o}} \right)+\mathrm{y}_{\mathrm{o}} \:\mathrm{passes}\:\mathrm{through}\:\left(\mathrm{0},\mathrm{18}\right) \\ $$$$\mathrm{18}\:=\:−\frac{\mathrm{1}}{\mathrm{2x}_{\mathrm{o}} }\left(−\mathrm{x}_{\mathrm{o}} \right)+\mathrm{y}_{\mathrm{o}} \Rightarrow\mathrm{y}_{\mathrm{o}} =\mathrm{18}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{35}}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}_{\mathrm{o}} =\:\pm\sqrt{\mathrm{y}_{\mathrm{o}} }\:=\:\pm\sqrt{\frac{\mathrm{35}}{\mathrm{2}}} \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{point}\:\mathrm{are}\:\left(\pm\sqrt{\frac{\mathrm{35}}{\mathrm{2}}},\:\frac{\mathrm{35}}{\mathrm{2}}\right)\: \\ $$
Answered by 1549442205PVT last updated on 07/Aug/20

$$ \\ $$$$\mathrm{Let}\:\mathrm{A}\:\left(\mathrm{x},\mathrm{x}^{\mathrm{2}} \right)\mathrm{be}\:\mathrm{any}\:\mathrm{point}\:\mathrm{lying}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{curve}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} .\mathrm{Then} \\ $$$$\mathrm{MA}=\sqrt{\left(\mathrm{x}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{2}} −\mathrm{18}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{35x}^{\mathrm{2}} +\mathrm{324}}=\sqrt{\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{35}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{71}}{\mathrm{4}}} \\ $$$$\geqslant\sqrt{\frac{\mathrm{71}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{71}}}{\mathrm{2}}. \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{when}\:\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{35}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{x}=\pm\sqrt{\frac{\mathrm{35}}{\mathrm{2}}}=\pm\frac{\sqrt{\mathrm{70}}}{\mathrm{2}}\Rightarrow\mathrm{y}=\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{35}}{\mathrm{2}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{point}\:\mathrm{lying}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{2}} \:\mathrm{which}\:\mathrm{is}\:\mathrm{nearest}\:\mathrm{point}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{point}\:\left(\mathrm{0};\mathrm{18}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{point}\:\mathrm{A}\left(\pm\frac{\sqrt{\mathrm{70}}}{\mathrm{2}};\frac{\mathrm{35}}{\mathrm{2}}\right) \\ $$$$\mathrm{and}\:\mathrm{that}\:\mathrm{shortest}\:\:\mathrm{distance}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\frac{\sqrt{\mathrm{71}}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 07/Aug/20
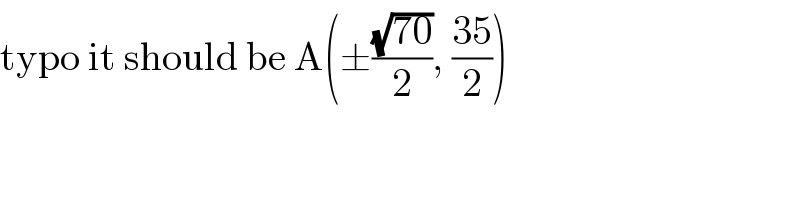
$$\mathrm{typo}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{A}\left(\pm\frac{\sqrt{\mathrm{70}}}{\mathrm{2}},\:\frac{\mathrm{35}}{\mathrm{2}}\right) \\ $$
Commented by 1549442205PVT last updated on 07/Aug/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{I}\:\mathrm{corrected} \\ $$
