
Question Number 108582 by mathmax by abdo last updated on 17/Aug/20
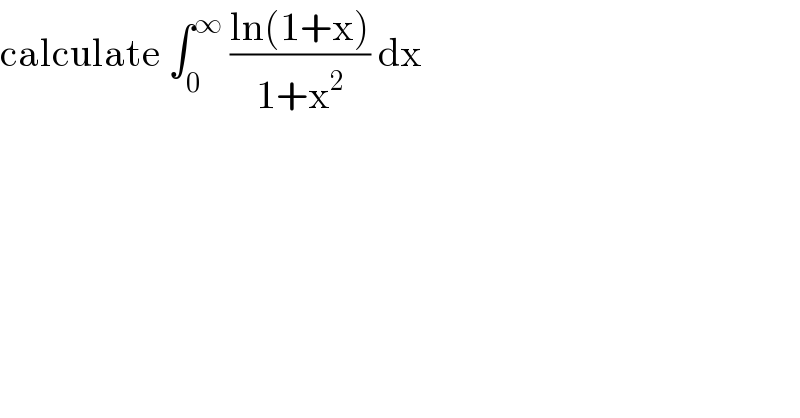
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 18/Aug/20
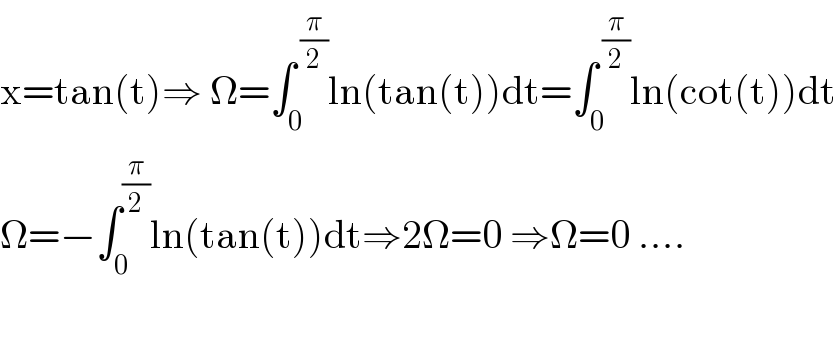
$$\mathrm{x}=\mathrm{tan}\left(\mathrm{t}\right)\Rightarrow\:\Omega=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{tan}\left(\mathrm{t}\right)\right)\mathrm{dt}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cot}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\Omega=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{tan}\left(\mathrm{t}\right)\right)\mathrm{dt}\Rightarrow\mathrm{2}\Omega=\mathrm{0}\:\Rightarrow\Omega=\mathrm{0}\:.... \\ $$$$\: \\ $$
Commented by Her_Majesty last updated on 18/Aug/20

$${how}??? \\ $$
Commented by mathmax by abdo last updated on 18/Aug/20

$$\mathrm{you}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 18/Aug/20
![I =∫_0 ^∞ ((ln(1+x))/(1+x^2 ))dx we do the changement x=tant ⇒ I =∫_0 ^(π/2) ((ln(1+tant))/(1+tan^2 t))(1+tan^2 t) dt =∫_0 ^(π/2) ln(1+tant)dt let f(a) =∫_0 ^(π/2) ln(a+tant)dt (a>0) ⇒ f^′ (a) =∫_0 ^(π/2) (dt/(a+tant)) =_(tant =u) ∫_0 ^∞ (du/((1+u^2 )(a+u))) let decompose F(u) =(1/((u+a)(u^2 +1))) ⇒F(u) =(α/(u+a)) +((βu +c)/(u^2 +1)) α =(1/(a^2 +1)) lim_(u→+∞) uF(u) =o =α+β ⇒β =−(1/(a^2 +1)) F(o) =(1/a) =(α/a) +c ⇒c =(1/a)−(1/(a(a^2 +1))) =(1/a){1−(1/(a^2 +1))} =(1/a)×(a^2 /(a^2 +1)) =(a/(a^2 +1)) ⇒F(u) =(1/((a^2 +1)(u+a)))+((−(1/(a^2 +1))u +(a/(a^2 +1)))/(u^2 +1)) ⇒f^′ (a) =(1/(a^2 +1)){ ∫_0 ^∞ (du/(u+a))−(1/2)∫_0 ^∞ ((2u)/(u^2 +1))du +a ∫_0 ^∞ (du/(u^2 +1))} =(1/(a^2 +1)){ [ln∣((u+a)/(√(u^2 +1)))∣]_0 ^(+∞) +((aπ)/2)} =−((lna)/(1+a^2 ))+(π/2)(a/(a^2 +1)) ⇒ f(a) =−∫_0 ^a ((lnz)/(1+z^2 ))dz +(π/2)∫_0 ^a ((zdz)/(z^2 +1))+c =(π/4)ln(a^2 +1)−∫_0 ^a ((lnz)/(1+z^2 ))dz +c c=f(0) =∫_0 ^(π/2) ln(((sint)/(cost)))dt =∫_0 ^(π/2) ln(sing)dt−∫_0 ^(π/2) ln(cost)dt =0 ⇒ f(a) =(π/4)ln(1+a^2 )−∫_0 ^a ((lnz)/(1+z^2 ))dz ⇒ f(1) =(π/4)ln(2)−∫_0 ^(1 ) ((lnz)/(1+z^2 ))dz but ∫_0 ^1 ((lnz)/(1+z^2 ))dz=∫_0 ^1 lnzΣ_(n=0) ^∞ (−1)^n z^(2n) dz=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 z^(2n) ln(z)dz =Σ_(n=0) ^∞ (−1)^n {[(z^(2n+1) /(2n+1)) lnz]_0 ^1 −(1/(2n+1))∫_0 ^1 z^(2n) dz} =−Σ_(n=0) ^∞ (−1)^n (1/((2n+1)^2 )) =−K ( catalan constant) ⇒ ∫_0 ^∞ ((ln(1+x))/(1+x^2 ))dx =((πln(2))/4) +K](Q108660.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{tant}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)\:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)\mathrm{dt}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{a}+\mathrm{tant}\right)\mathrm{dt}\:\:\left(\mathrm{a}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{a}+\mathrm{tant}}\:\:=_{\mathrm{tant}\:=\mathrm{u}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{a}+\mathrm{u}\right)}\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{u}+\mathrm{a}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\alpha}{\mathrm{u}+\mathrm{a}}\:+\frac{\beta\mathrm{u}\:+\mathrm{c}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha\:=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:\:\:\:\:\:\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \mathrm{uF}\left(\mathrm{u}\right)\:=\mathrm{o}\:=\alpha+\beta\:\Rightarrow\beta\:=−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{F}\left(\mathrm{o}\right)\:=\frac{\mathrm{1}}{\mathrm{a}}\:=\frac{\alpha}{\mathrm{a}}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{a}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{a}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}×\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{u}+\mathrm{a}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{u}\:+\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\left\{\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{u}+\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:+\mathrm{a}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\left\{\:\left[\mathrm{ln}\mid\frac{\mathrm{u}+\mathrm{a}}{\sqrt{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}}\mid\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{a}\pi}{\mathrm{2}}\right\}\:=−\frac{\mathrm{lna}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }+\frac{\pi}{\mathrm{2}}\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{lnz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\mathrm{dz}\:+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{zdz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}+\mathrm{c}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)−\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{lnz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\mathrm{dz}\:+\mathrm{c} \\ $$$$\mathrm{c}=\mathrm{f}\left(\mathrm{0}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\frac{\mathrm{sint}}{\mathrm{cost}}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sing}\right)\mathrm{dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cost}\right)\mathrm{dt}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{lnz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\mathrm{dz}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{lnz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\mathrm{dz}\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\mathrm{dz}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{lnz}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}} \:\mathrm{dz}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{z}^{\mathrm{2n}} \:\mathrm{ln}\left(\mathrm{z}\right)\mathrm{dz} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\left[\frac{\mathrm{z}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\:\mathrm{lnz}\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{z}^{\mathrm{2n}} \:\mathrm{dz}\right\} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:=−\mathrm{K}\:\:\left(\:\mathrm{catalan}\:\mathrm{constant}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:+\mathrm{K} \\ $$
