Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 111620 by mathdave last updated on 04/Sep/20

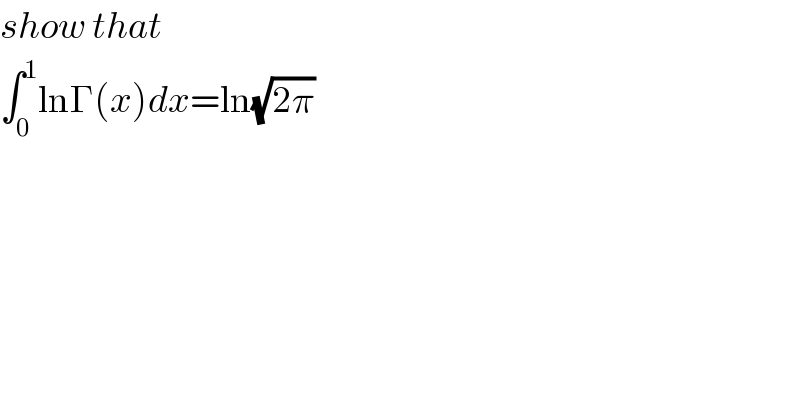
show that ∫_0 ^1 lnΓ(x)dx=ln(√(2π))

$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left({x}\right){dx}=\mathrm{ln}\sqrt{\mathrm{2}\pi} \\ $$

Answered by mathmax by abdo last updated on 04/Sep/20

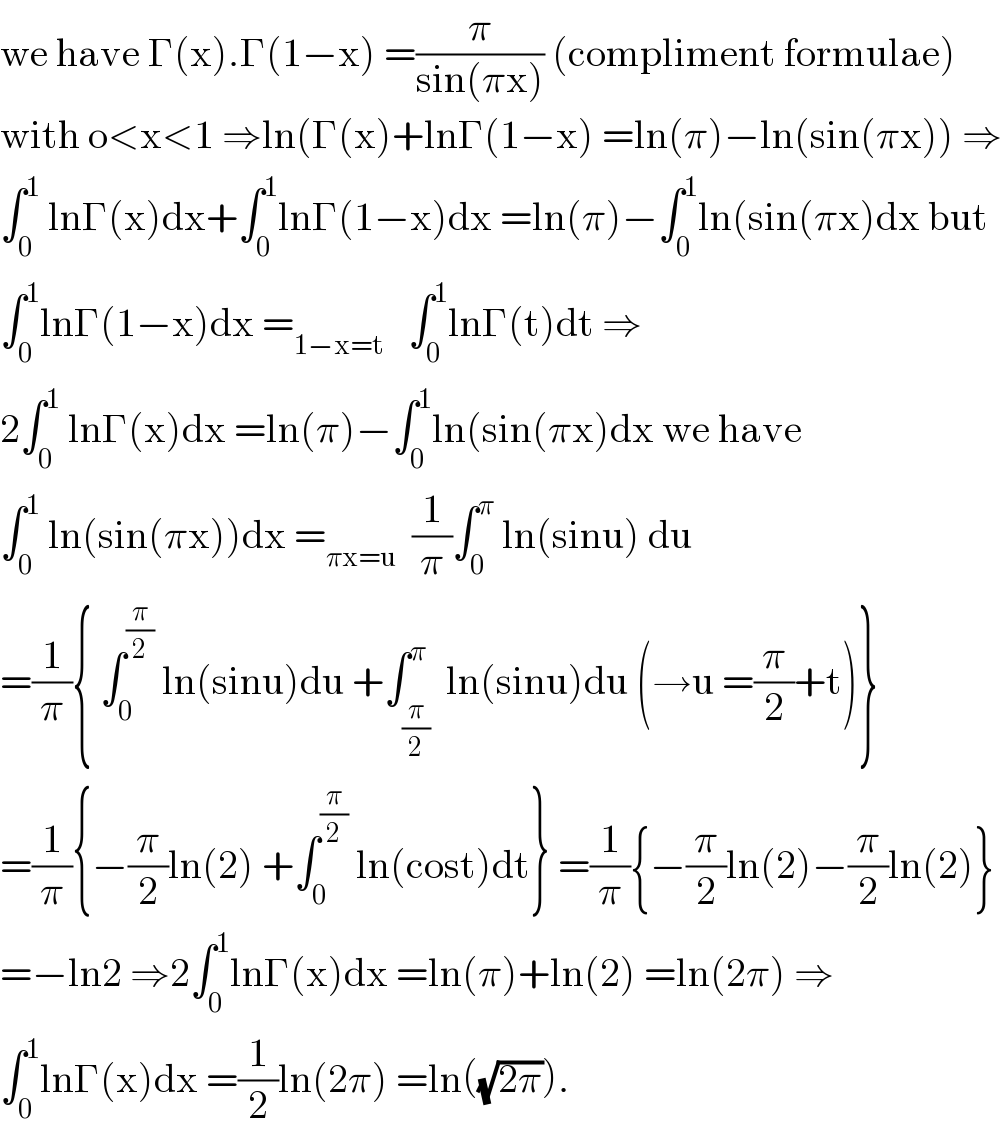
we have Γ(x).Γ(1−x) =(π/(sin(πx))) (compliment formulae) with o<x<1 ⇒ln(Γ(x)+lnΓ(1−x) =ln(π)−ln(sin(πx)) ⇒ ∫_0 ^1 lnΓ(x)dx+∫_0 ^1 lnΓ(1−x)dx =ln(π)−∫_0 ^1 ln(sin(πx)dx but ∫_0 ^1 lnΓ(1−x)dx =_(1−x=t) ∫_0 ^1 lnΓ(t)dt ⇒ 2∫_0 ^1 lnΓ(x)dx =ln(π)−∫_0 ^1 ln(sin(πx)dx we have ∫_0 ^1 ln(sin(πx))dx =_(πx=u) (1/π)∫_0 ^π ln(sinu) du =(1/π){ ∫_0 ^(π/2) ln(sinu)du +∫_(π/2) ^π ln(sinu)du (→u =(π/2)+t)} =(1/π){−(π/2)ln(2) +∫_0 ^(π/2) ln(cost)dt} =(1/π){−(π/2)ln(2)−(π/2)ln(2)} =−ln2 ⇒2∫_0 ^1 lnΓ(x)dx =ln(π)+ln(2) =ln(2π) ⇒ ∫_0 ^1 lnΓ(x)dx =(1/2)ln(2π) =ln((√(2π))).

$$\mathrm{we}\:\mathrm{have}\:\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{1}−\mathrm{x}\right)\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{x}\right)}\:\left(\mathrm{compliment}\:\mathrm{formulae}\right) \\ $$$$\mathrm{with}\:\mathrm{o}<\mathrm{x}<\mathrm{1}\:\Rightarrow\mathrm{ln}\left(\Gamma\left(\mathrm{x}\right)+\mathrm{ln}\Gamma\left(\mathrm{1}−\mathrm{x}\right)\:=\mathrm{ln}\left(\pi\right)−\mathrm{ln}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\:\Rightarrow\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\Gamma\left(\mathrm{x}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:=\mathrm{ln}\left(\pi\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\mathrm{dx}\:\mathrm{but}\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:=_{\mathrm{1}−\mathrm{x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left(\mathrm{t}\right)\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\Gamma\left(\mathrm{x}\right)\mathrm{dx}\:=\mathrm{ln}\left(\pi\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\mathrm{dx}\:\mathrm{we}\:\mathrm{have}\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\mathrm{dx}\:=_{\pi\mathrm{x}=\mathrm{u}} \:\:\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} \:\mathrm{ln}\left(\mathrm{sinu}\right)\:\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\pi}\left\{\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{sinu}\right)\mathrm{du}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{ln}\left(\mathrm{sinu}\right)\mathrm{du}\:\left(\rightarrow\mathrm{u}\:=\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\pi}\left\{−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cost}\right)\mathrm{dt}\right\}\:=\frac{\mathrm{1}}{\pi}\left\{−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\right\} \\ $$$$=−\mathrm{ln2}\:\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left(\mathrm{x}\right)\mathrm{dx}\:=\mathrm{ln}\left(\pi\right)+\mathrm{ln}\left(\mathrm{2}\right)\:=\mathrm{ln}\left(\mathrm{2}\pi\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\Gamma\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\pi\right)\:=\mathrm{ln}\left(\sqrt{\mathrm{2}\pi}\right). \\ $$

Commented by mnjuly1970 last updated on 06/Sep/20

thank you so much ′ sir′ for your effort ...

$${thank}\:{you}\:{so}\:{much}\:'\:{sir}'\:{for} \\ $$$${your}\:\:{effort}\:... \\ $$

Commented by Tawa11 last updated on 06/Sep/21

great sir

$$\mathrm{great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com