
Question Number 112478 by dw last updated on 08/Sep/20
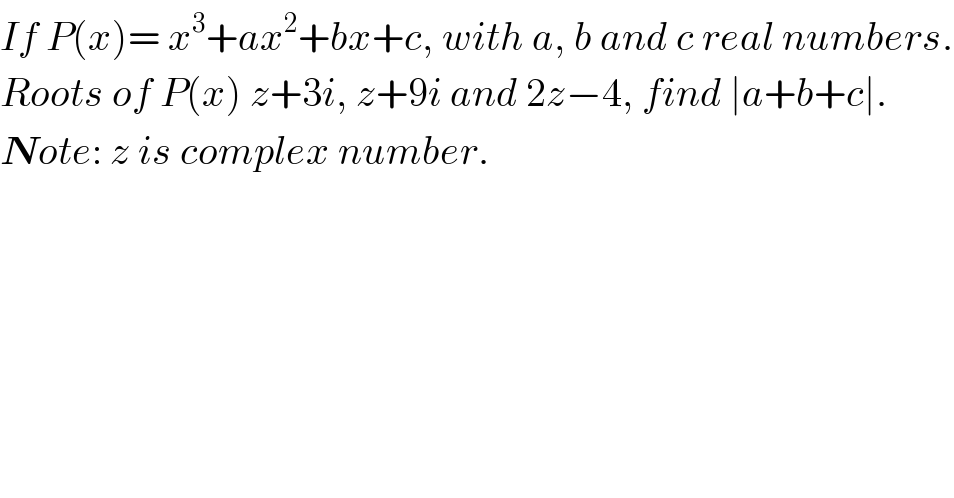
$${If}\:{P}\left({x}\right)=\:{x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c},\:{with}\:{a},\:{b}\:{and}\:{c}\:{real}\:{numbers}. \\ $$$${Roots}\:{of}\:{P}\left({x}\right)\:{z}+\mathrm{3}{i},\:{z}+\mathrm{9}{i}\:{and}\:\mathrm{2}{z}−\mathrm{4},\:{find}\:\mid{a}+{b}+{c}\mid. \\ $$$$\boldsymbol{{N}}{ote}:\:{z}\:{is}\:{complex}\:{number}. \\ $$
Answered by floor(10²Eta[1]) last updated on 08/Sep/20
![we know that a cubic polynomial with real coefficients can have: 3 real roots or 1 real root and 2 complex roots because if a polynomial has a complex root, the conjugate of this complex number is also a root. If z∈R⇒2z−4∈R, but if z+3i and z+9i are the complex roots so z−3i and z−9i also should be. But that′s impossible because we just have 3 roots. So z have an imaginary part⇒2z−4 is one of the complex roots. z=u+vi roots: [2u−4+2vi], [u+(3+v)i], [u+(9+v)i] 1 case: u+(9+v)i is the real root: ⇒9+v=0∴v=−9 so (2u−4−18i) is the conjugate of (u−6i) but this is impossible because the imaginary parts are different. 2 case: u+(3+v)i is the real root: ⇒3+v=0∴v=−3 so (2u−4−6i) is the conjugate of (u+6i) ⇒2u−4=u∴u=4 roots: (4), (4+6i), (4−6i) ⇒P(x)=(x−4)(x−4−6i)(x−4+6i) P(1)=1+a+b+c =−3(−3−6i)(−3+6i)=−3.45 ⇒a+b+c=−135−1=−136 ∣a+b+c∣=136.](Q112483.png)
$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{a}\:\mathrm{cubic}\:\mathrm{polynomial}\:\mathrm{with} \\ $$$$\mathrm{real}\:\mathrm{coefficients}\:\mathrm{can}\:\mathrm{have}: \\ $$$$\mathrm{3}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{or}\:\mathrm{1}\:\mathrm{real}\:\mathrm{root}\:\mathrm{and}\:\mathrm{2}\:\mathrm{complex}\:\mathrm{roots} \\ $$$$\mathrm{because}\:\mathrm{if}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{has}\:\mathrm{a}\:\mathrm{complex}\: \\ $$$$\mathrm{root},\:\mathrm{the}\:\mathrm{conjugate}\:\mathrm{of}\:\mathrm{this}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{root}. \\ $$$$\mathrm{If}\:\mathrm{z}\in\mathbb{R}\Rightarrow\mathrm{2z}−\mathrm{4}\in\mathbb{R},\:\mathrm{but}\:\mathrm{if}\:\mathrm{z}+\mathrm{3i}\:\mathrm{and}\:\mathrm{z}+\mathrm{9i} \\ $$$$\mathrm{are}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{roots}\:\mathrm{so}\:\mathrm{z}−\mathrm{3i}\:\mathrm{and}\:\mathrm{z}−\mathrm{9i} \\ $$$$\mathrm{also}\:\mathrm{should}\:\mathrm{be}.\:\mathrm{But}\:\mathrm{that}'\mathrm{s}\:\mathrm{impossible} \\ $$$$\mathrm{because}\:\mathrm{we}\:\mathrm{just}\:\mathrm{have}\:\mathrm{3}\:\mathrm{roots}. \\ $$$$\mathrm{So}\:\mathrm{z}\:\mathrm{have}\:\mathrm{an}\:\mathrm{imaginary}\:\mathrm{part}\Rightarrow\mathrm{2z}−\mathrm{4} \\ $$$$\mathrm{is}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{roots}. \\ $$$$\mathrm{z}=\mathrm{u}+\mathrm{vi} \\ $$$$\mathrm{roots}:\:\left[\mathrm{2u}−\mathrm{4}+\mathrm{2vi}\right],\:\left[\mathrm{u}+\left(\mathrm{3}+\mathrm{v}\right)\mathrm{i}\right],\:\left[\mathrm{u}+\left(\mathrm{9}+\mathrm{v}\right)\mathrm{i}\right] \\ $$$$\mathrm{1}\:\mathrm{case}: \\ $$$$\mathrm{u}+\left(\mathrm{9}+\mathrm{v}\right)\mathrm{i}\:\mathrm{is}\:\mathrm{the}\:\mathrm{real}\:\mathrm{root}: \\ $$$$\Rightarrow\mathrm{9}+\mathrm{v}=\mathrm{0}\therefore\mathrm{v}=−\mathrm{9} \\ $$$$\mathrm{so}\:\left(\mathrm{2u}−\mathrm{4}−\mathrm{18i}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{conjugate}\:\mathrm{of}\:\left(\mathrm{u}−\mathrm{6i}\right) \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{impossible}\:\mathrm{because}\:\mathrm{the} \\ $$$$\mathrm{imaginary}\:\mathrm{parts}\:\mathrm{are}\:\mathrm{different}. \\ $$$$\mathrm{2}\:\mathrm{case}: \\ $$$$\mathrm{u}+\left(\mathrm{3}+\mathrm{v}\right)\mathrm{i}\:\mathrm{is}\:\mathrm{the}\:\mathrm{real}\:\mathrm{root}: \\ $$$$\Rightarrow\mathrm{3}+\mathrm{v}=\mathrm{0}\therefore\mathrm{v}=−\mathrm{3} \\ $$$$\mathrm{so}\:\left(\mathrm{2u}−\mathrm{4}−\mathrm{6i}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{conjugate}\:\mathrm{of}\:\left(\mathrm{u}+\mathrm{6i}\right) \\ $$$$\Rightarrow\mathrm{2u}−\mathrm{4}=\mathrm{u}\therefore\mathrm{u}=\mathrm{4} \\ $$$$\mathrm{roots}:\:\left(\mathrm{4}\right),\:\left(\mathrm{4}+\mathrm{6i}\right),\:\left(\mathrm{4}−\mathrm{6i}\right) \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}−\mathrm{4}−\mathrm{6i}\right)\left(\mathrm{x}−\mathrm{4}+\mathrm{6i}\right) \\ $$$$\mathrm{P}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{a}+\mathrm{b}+\mathrm{c} \\ $$$$=−\mathrm{3}\left(−\mathrm{3}−\mathrm{6i}\right)\left(−\mathrm{3}+\mathrm{6i}\right)=−\mathrm{3}.\mathrm{45} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}=−\mathrm{135}−\mathrm{1}=−\mathrm{136} \\ $$$$\mid\mathrm{a}+\mathrm{b}+\mathrm{c}\mid=\mathrm{136}. \\ $$
Commented by MJS_new last updated on 08/Sep/20

$$\mathrm{good}\:\mathrm{job}! \\ $$
Commented by dw last updated on 09/Sep/20

$${Thank}\:{you}\:{Sir} \\ $$
