
Question Number 112971 by ajfour last updated on 10/Sep/20
Commented by ajfour last updated on 11/Sep/20

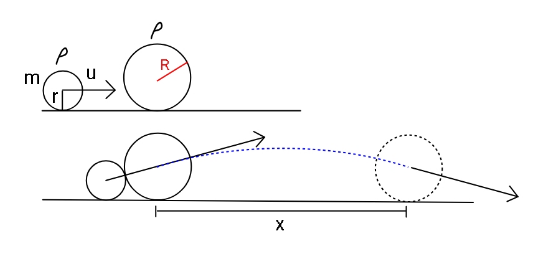
$${A}\:{small}\:{sphere}\:{of}\:{radius}\:{r},\:{mass}\:{m}, \\ $$$${collides}\:{elastically}\:{with}\:{another}\: \\ $$$${sphere}\:{of}\:{same}\:{density}\:{as}\:{that}\:{of} \\ $$$${smaller}\:{sphere}.\:{Find}\:{radius}\:{of} \\ $$$${larger}\:{sphere}\:{such}\:{that}\:{its}\:{range} \\ $$$${x}\:{be}\:{maximum}. \\ $$$$\:\:\:\:\: \\ $$
Answered by mr W last updated on 12/Sep/20

Commented by mr W last updated on 12/Sep/20
![M=((R/r))^3 m sin θ=((R−r)/(R+r))=1−(2/((R/r)+1)) ⇒(R/r)=(2/(1−sin θ))−1 mu=MV cos θ+mv ⇒u=((R/r))^3 V cos θ+v ((mu^2 )/2)=((MV^2 )/2)+((mv^2 )/2) ⇒u^2 =((R/r))^3 V^2 +v^2 ⇒u^2 =((R/r))^3 V^2 +[u−((R/r))^3 cos θ V]^2 ⇒[1+((R/r))^3 cos^2 θ]V=2u cos θ ⇒V=((2u cos θ)/(1+((R/r))^3 cos^2 θ)) 0=V sin θ ×(x/(V cos θ))−(g/2)((x/(V cos θ)))^2 ⇒gx=sin 2θ V^2 ⇒gx=sin 2θ[((2u cos θ)/(1+((R/r))^3 cos^2 θ))]^2 ⇒((gx)/(8u^2 ))=((sin θ cos^3 θ)/([1+((R/r))^3 cos^2 θ]^2 )) ⇒((gx)/(8u^2 ))=((sin θ cos^3 θ)/([1+((2/(1−sin θ))−1)^3 cos^2 θ]^2 )) x_(max) is at θ=6.9827° or (R/r)=1.277](Q113286.png)
$${M}=\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {m} \\ $$$$\mathrm{sin}\:\theta=\frac{{R}−{r}}{{R}+{r}}=\mathrm{1}−\frac{\mathrm{2}}{\frac{{R}}{{r}}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{R}}{{r}}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{sin}\:\theta}−\mathrm{1} \\ $$$${mu}={MV}\:\mathrm{cos}\:\theta+{mv} \\ $$$$\Rightarrow{u}=\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {V}\:\mathrm{cos}\:\theta+{v} \\ $$$$\frac{{mu}^{\mathrm{2}} }{\mathrm{2}}=\frac{{MV}^{\mathrm{2}} }{\mathrm{2}}+\frac{{mv}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {V}^{\mathrm{2}} +{v}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {V}^{\mathrm{2}} +\left[{u}−\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \mathrm{cos}\:\theta\:{V}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\left[\mathrm{1}+\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \:\theta\right]{V}=\mathrm{2}{u}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{V}=\frac{\mathrm{2}{u}\:\mathrm{cos}\:\theta}{\mathrm{1}+\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{0}={V}\:\mathrm{sin}\:\theta\:×\frac{{x}}{{V}\:\mathrm{cos}\:\theta}−\frac{{g}}{\mathrm{2}}\left(\frac{{x}}{{V}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{gx}=\mathrm{sin}\:\mathrm{2}\theta\:{V}^{\mathrm{2}} \\ $$$$\Rightarrow{gx}=\mathrm{sin}\:\mathrm{2}\theta\left[\frac{\mathrm{2}{u}\:\mathrm{cos}\:\theta}{\mathrm{1}+\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \:\theta}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{gx}}{\mathrm{8}{u}^{\mathrm{2}} }=\frac{\mathrm{sin}\:\theta\:\mathrm{cos}^{\mathrm{3}} \:\theta}{\left[\mathrm{1}+\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \:\theta\right]^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{gx}}{\mathrm{8}{u}^{\mathrm{2}} }=\frac{\mathrm{sin}\:\theta\:\mathrm{cos}^{\mathrm{3}} \:\theta}{\left[\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{sin}\:\theta}−\mathrm{1}\right)^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \:\theta\right]^{\mathrm{2}} } \\ $$$$ \\ $$$${x}_{{max}} \:{is}\:{at}\:\theta=\mathrm{6}.\mathrm{9827}° \\ $$$${or}\:\frac{{R}}{{r}}=\mathrm{1}.\mathrm{277} \\ $$
Commented by mr W last updated on 13/Sep/20

$${to}\:{be}\:{honest},\:{i}'{m}\:{not}\:{sure}\:{if}\:{it}'{s} \\ $$$${correct}\:{to}\:{take}\:{the}\:{direction}\:{of}\:{V} \\ $$$${at}\:{angle}\:\theta. \\ $$
Commented by ajfour last updated on 14/Sep/20
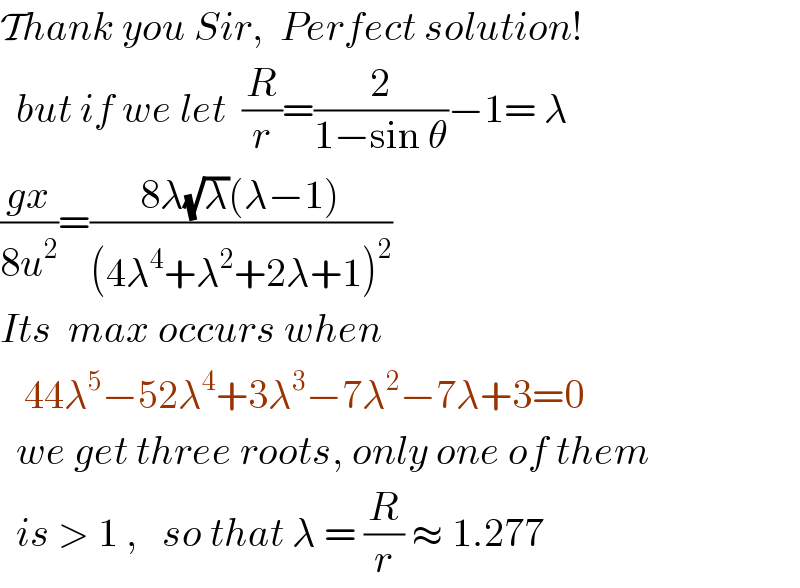
$$\mathcal{T}{hank}\:{you}\:{Sir},\:\:{Perfect}\:{solution}! \\ $$$$\:\:{but}\:{if}\:{we}\:{let}\:\:\frac{{R}}{{r}}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{sin}\:\theta}−\mathrm{1}=\:\lambda \\ $$$$\frac{{gx}}{\mathrm{8}{u}^{\mathrm{2}} }=\frac{\mathrm{8}\lambda\sqrt{\lambda}\left(\lambda−\mathrm{1}\right)}{\left(\mathrm{4}\lambda^{\mathrm{4}} +\lambda^{\mathrm{2}} +\mathrm{2}\lambda+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Its}\:\:{max}\:{occurs}\:{when} \\ $$$$\:\:\:\mathrm{44}\lambda^{\mathrm{5}} −\mathrm{52}\lambda^{\mathrm{4}} +\mathrm{3}\lambda^{\mathrm{3}} −\mathrm{7}\lambda^{\mathrm{2}} −\mathrm{7}\lambda+\mathrm{3}=\mathrm{0} \\ $$$$\:\:{we}\:{get}\:{three}\:{roots},\:{only}\:{one}\:{of}\:{them} \\ $$$$\:\:{is}\:>\:\mathrm{1}\:,\:\:\:{so}\:{that}\:\lambda\:=\:\frac{{R}}{{r}}\:\approx\:\mathrm{1}.\mathrm{277}\: \\ $$
Commented by mr W last updated on 14/Sep/20

$${great}! \\ $$
