Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 113857 by ayenisamuel last updated on 15/Sep/20

find the values of k for which the line y=kx−3 does not meet the curve y=2x^2 −3x+k.

$${find}\:{the}\:{values}\:{of}\:{k}\:{for}\:{which}\:{the} \\ $$$${line}\:{y}={kx}−\mathrm{3}\:{does}\:{not}\:{meet}\:{the}\:{curve} \\ $$$${y}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k}. \\ $$

Answered by MJS_new last updated on 15/Sep/20

first, intersect them kx−3=2x^2 −3x+k x^2 −((k+3)/2)x+((k+3)/2)=0 let x=t+((k+3)/4) and solve for t^2 t^2 =(((k−5)(k+3))/(16)) ⇒ if (((k−5)(k+3))/(16))<0 ⇒ no solution ⇒ −3<k<5 is the answer

$$\mathrm{first},\:\mathrm{intersect}\:\mathrm{them} \\ $$$${kx}−\mathrm{3}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k} \\ $$$${x}^{\mathrm{2}} −\frac{{k}+\mathrm{3}}{\mathrm{2}}{x}+\frac{{k}+\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={t}+\frac{{k}+\mathrm{3}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:{t}^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} =\frac{\left({k}−\mathrm{5}\right)\left({k}+\mathrm{3}\right)}{\mathrm{16}} \\ $$$$\Rightarrow\:\mathrm{if}\:\frac{\left({k}−\mathrm{5}\right)\left({k}+\mathrm{3}\right)}{\mathrm{16}}<\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\Rightarrow\:−\mathrm{3}<{k}<\mathrm{5}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer} \\ $$

Answered by 1549442205PVT last updated on 16/Sep/20

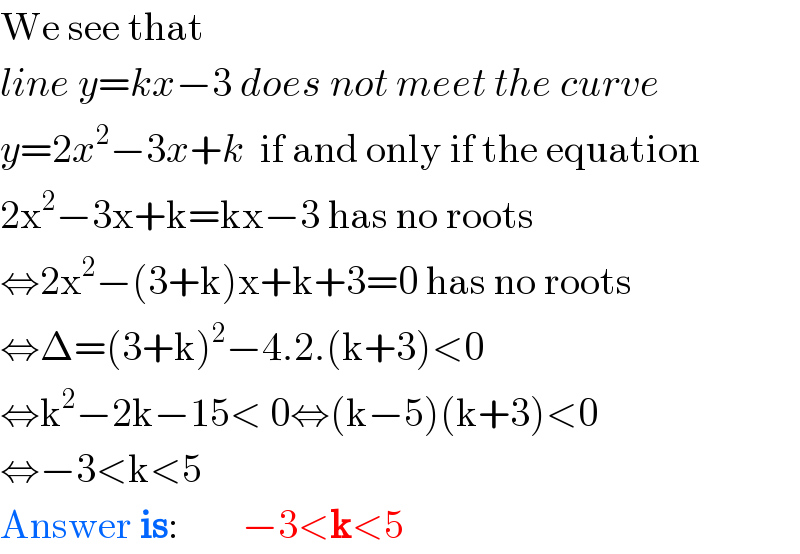
We see that line y=kx−3 does not meet the curve y=2x^2 −3x+k if and only if the equation 2x^2 −3x+k=kx−3 has no roots ⇔2x^2 −(3+k)x+k+3=0 has no roots ⇔Δ=(3+k)^2 −4.2.(k+3)<0 ⇔k^2 −2k−15< 0⇔(k−5)(k+3)<0 ⇔−3<k<5 Answer is: −3<k<5

$$\mathrm{We}\:\mathrm{see}\:\mathrm{that} \\ $$$${line}\:{y}={kx}−\mathrm{3}\:{does}\:{not}\:{meet}\:{the}\:{curve} \\ $$$${y}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k}\:\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{k}=\mathrm{kx}−\mathrm{3}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} −\left(\mathrm{3}+\mathrm{k}\right)\mathrm{x}+\mathrm{k}+\mathrm{3}=\mathrm{0}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\Leftrightarrow\Delta=\left(\mathrm{3}+\mathrm{k}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{2}.\left(\mathrm{k}+\mathrm{3}\right)<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{k}^{\mathrm{2}} −\mathrm{2k}−\mathrm{15}<\:\mathrm{0}\Leftrightarrow\left(\mathrm{k}−\mathrm{5}\right)\left(\mathrm{k}+\mathrm{3}\right)<\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{3}<\mathrm{k}<\mathrm{5} \\ $$$$\mathrm{Answer}\:\boldsymbol{\mathrm{is}}:\:\:\:\:\:\:\:\:−\mathrm{3}<\boldsymbol{\mathrm{k}}<\mathrm{5} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com