
Question Number 113867 by Ar Brandon last updated on 15/Sep/20
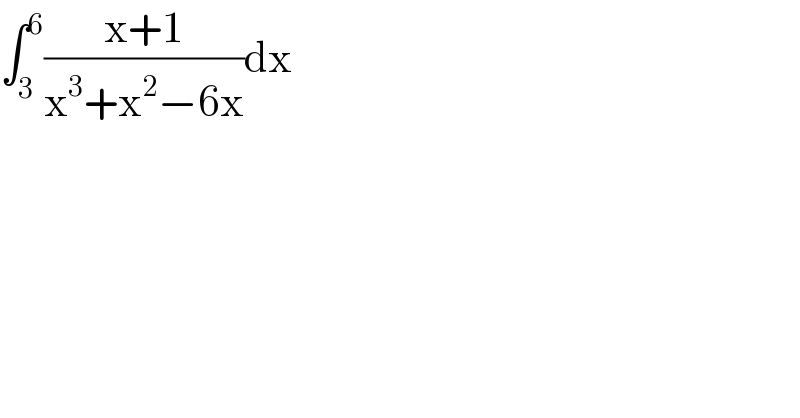
$$\int_{\mathrm{3}} ^{\mathrm{6}} \frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{6x}}\mathrm{dx} \\ $$
Answered by abdomsup last updated on 15/Sep/20
![I =∫_3 ^6 ((x+1)/(x^3 +x^2 −6x))dx let decompise F(x)=((x+1)/(x^3 +x^2 −6x)) ⇒ F(x) =((x+1)/(x(x^2 +x−6))) x^2 +x−6=0→Δ=1+24=25 x_1 =((−1+5)/2)=2 and x_2 =((−1−5)/2)=−3 ⇒F(x)=((x+1)/(x(x−2)(x+3))) =(a/x) +(b/(x−2)) +(c/(x+3)) a=−(1/6) , b=(3/(2(6))) =(1/4) c=((−2)/((−3)(−5))) =(2/(15)) ⇒ F(x)=−(1/(6x)) +(1/(4(x−2))) +(2/(15(x+3))) ⇒I =∫_3 ^6 (−(1/(6x)) +(1/(4(x−2)))+(2/(15(x+3))))dx =−(1/6)[ln∣x∣]_3 ^6 +(1/4)[ln∣x−2∣]_3 ^6 +(2/(15))[ln∣x+3∣]_3 ^6 =−(1/6)ln(2)+(1/4)(2ln2) +(2/(15)){2ln(3)−ln(6)} =((1/2)−(1/6))ln(2)+(2/(15)){ln(3)−ln(2)} =((1/3)−(2/(15)))ln(2)+(2/(15))ln(3) =(1/5)ln(2)+(2/(15))ln(3)](Q113870.png)
$${I}\:=\int_{\mathrm{3}} ^{\mathrm{6}} \:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} −\mathrm{6}{x}}{dx}\:{let}\:{decompise} \\ $$$${F}\left({x}\right)=\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} −\mathrm{6}{x}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{x}+\mathrm{1}}{{x}\left({x}^{\mathrm{2}} \:+{x}−\mathrm{6}\right)} \\ $$$${x}^{\mathrm{2}} \:+{x}−\mathrm{6}=\mathrm{0}\rightarrow\Delta=\mathrm{1}+\mathrm{24}=\mathrm{25} \\ $$$${x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}=\mathrm{2}\:{and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}=−\mathrm{3} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{{x}+\mathrm{1}}{{x}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)} \\ $$$$=\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{2}}\:+\frac{{c}}{{x}+\mathrm{3}} \\ $$$${a}=−\frac{\mathrm{1}}{\mathrm{6}}\:,\:{b}=\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{6}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${c}=\frac{−\mathrm{2}}{\left(−\mathrm{3}\right)\left(−\mathrm{5}\right)}\:=\frac{\mathrm{2}}{\mathrm{15}}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{6}{x}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{2}\right)}\:+\frac{\mathrm{2}}{\mathrm{15}\left({x}+\mathrm{3}\right)} \\ $$$$\Rightarrow{I}\:=\int_{\mathrm{3}} ^{\mathrm{6}} \left(−\frac{\mathrm{1}}{\mathrm{6}{x}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{2}\right)}+\frac{\mathrm{2}}{\mathrm{15}\left({x}+\mathrm{3}\right)}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\left[{ln}\mid{x}\mid\right]_{\mathrm{3}} ^{\mathrm{6}} \:+\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid{x}−\mathrm{2}\mid\right]_{\mathrm{3}} ^{\mathrm{6}} \\ $$$$+\frac{\mathrm{2}}{\mathrm{15}}\left[{ln}\mid{x}+\mathrm{3}\mid\right]_{\mathrm{3}} ^{\mathrm{6}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{ln}\mathrm{2}\right) \\ $$$$+\frac{\mathrm{2}}{\mathrm{15}}\left\{\mathrm{2}{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{6}\right)\right\} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}\right){ln}\left(\mathrm{2}\right)+\frac{\mathrm{2}}{\mathrm{15}}\left\{{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{2}\right)\right\} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{15}}\right){ln}\left(\mathrm{2}\right)+\frac{\mathrm{2}}{\mathrm{15}}{ln}\left(\mathrm{3}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{ln}\left(\mathrm{2}\right)+\frac{\mathrm{2}}{\mathrm{15}}{ln}\left(\mathrm{3}\right) \\ $$
