Question Number 113910 by bobhans last updated on 16/Sep/20

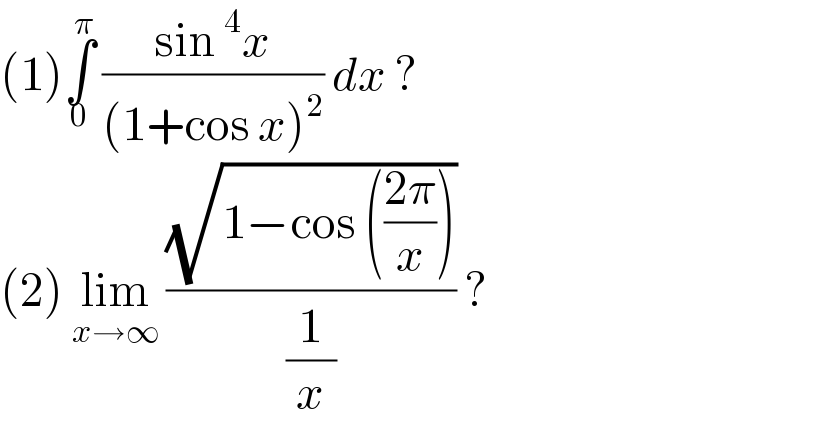
(1)∫_0 ^π ((sin ^4 x)/((1+cos x)^2 )) dx ? (2) lim_(x→∞) ((√(1−cos (((2π)/x))))/(1/x)) ?

Answered by bemath last updated on 16/Sep/20

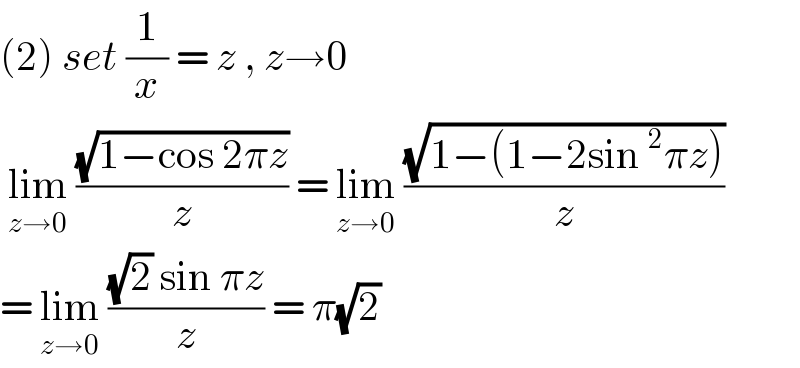
(2) set (1/x) = z , z→0 lim_(z→0) ((√(1−cos 2πz))/z) = lim_(z→0) ((√(1−(1−2sin ^2 πz)))/z) = lim_(z→0) (((√2) sin πz)/z) = π(√2)

Answered by 1549442205PVT last updated on 16/Sep/20

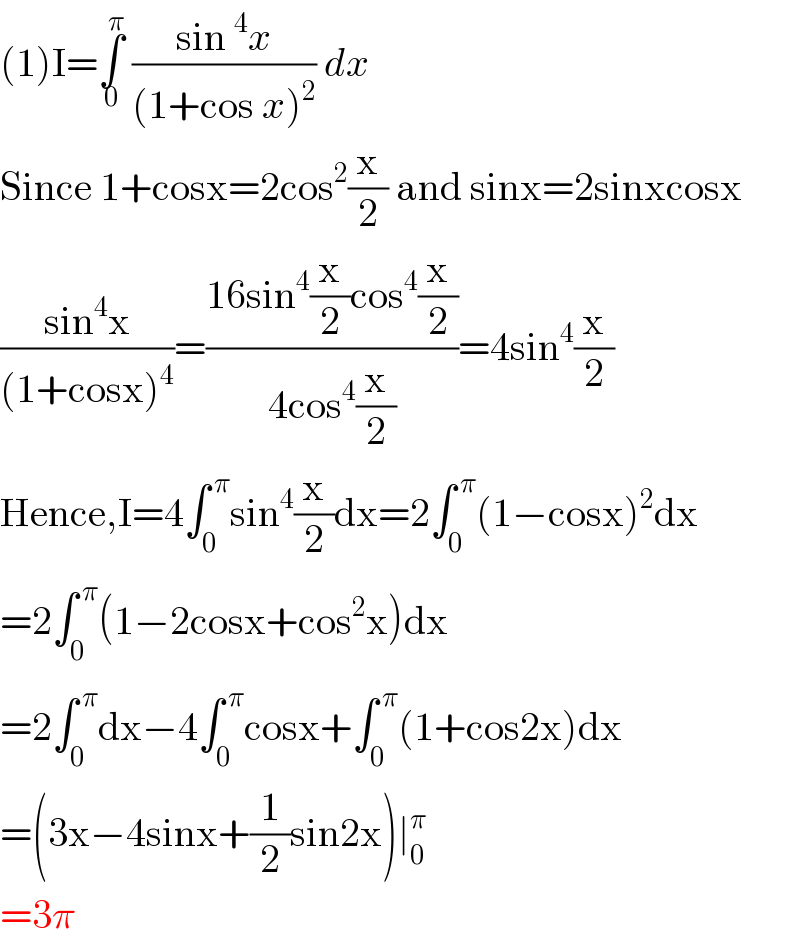
(1)I=∫_0 ^π ((sin ^4 x)/((1+cos x)^2 )) dx Since 1+cosx=2cos^2 (x/2) and sinx=2sinxcosx ((sin^4 x)/((1+cosx)^4 ))=((16sin^4 (x/2)cos^4 (x/2))/(4cos^4 (x/2)))=4sin^4 (x/2) Hence,I=4∫_0 ^( π) sin^4 (x/2)dx=2∫_0 ^( π) (1−cosx)^2 dx =2∫_0 ^( π) (1−2cosx+cos^2 x)dx =2∫_0 ^( π) dx−4∫_0 ^( π) cosx+∫_0 ^( π) (1+cos2x)dx =(3x−4sinx+(1/2)sin2x)∣_0 ^π =3π

Answered by MJS_new last updated on 16/Sep/20

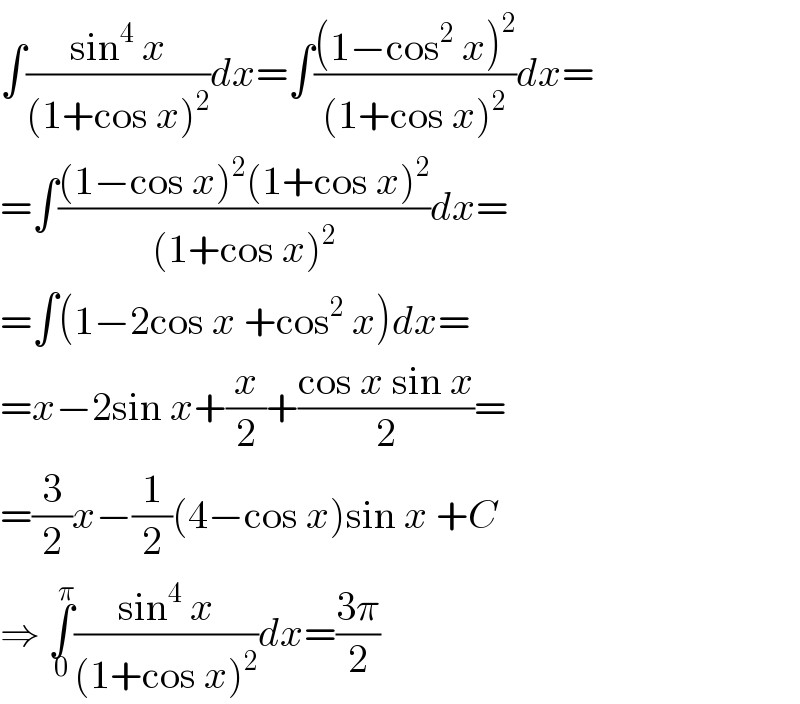
∫((sin^4 x)/((1+cos x)^2 ))dx=∫(((1−cos^2 x)^2 )/((1+cos x)^2 ))dx= =∫(((1−cos x)^2 (1+cos x)^2 )/((1+cos x)^2 ))dx= =∫(1−2cos x +cos^2 x)dx= =x−2sin x+(x/2)+((cos x sin x)/2)= =(3/2)x−(1/2)(4−cos x)sin x +C ⇒ ∫_0 ^π ((sin^4 x)/((1+cos x)^2 ))dx=((3π)/2)

Answered by mathmax by abdo last updated on 17/Sep/20

1) A =∫_0 ^π ((sin^4 x)/((1+cosx)^2 ))dx ⇒A =∫_0 ^π (((2sin((x/2))cos((x/2)))^4 )/((2cos^2 ((x/2)))^2 )) dx =4∫_0 ^π ((sin^4 ((x/2)) cos^4 ((x/2)))/(cos^4 ((x/2)))) dx =4 ∫_0 ^π sin^4 ((x/2))dx =_((x/2)=t) 8∫_0 ^(π/2) sin^4 (t) dt =8 ∫_0 ^(π/2) (((1−cos(2t))/2))^2 dt =2 ∫_0 ^(π/2) (1−2cos(2t) +cos^2 (2t))dt =2 [t−sin(2t)]_0 ^(π/2) +∫_0 ^(π/2) (1+cos(4t))dt =2{(π/2)} +(π/2) =π +(π/2) ⇒A =((3π)/2)