Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 113913 by Aina Samuel Temidayo last updated on 16/Sep/20

Find the square root of (√(50))+(√(48))

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{square}\:\mathrm{root}\:\mathrm{of}\:\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}} \\ $$

Answered by 1549442205PVT last updated on 16/Sep/20

We have ((√(50))+(√(48)))^2 =98+2(√(50.48)) =98+2(√(25.16.6))=98+40(√6) Hence (√((√(50))+(√(48))))=^4 (√(((√(50))+(√(48)))^2 )) =^4 (√(98+40(√6)))=^4 (√((a(√2)+b(√3))^4 )) (1) We need find a,b so that 98+40(√6)=(a(√2)+b(√3))^4 =4a^4 +8a^3 (√2).b(√3)+6.2a^2 .3b^2 +4.3b^3 (√3).a(√2) +9b^4 =(4a^4 +9b^4 +36a^2 b^2 +(8a^3 b+12ab^3 )(√6) ⇔ { ((4a^4 +36a^2 b^2 +9b^4 =98)),((8a^3 b+12ab^3 =40)) :} ⇔ { ((4a^4 +36a^2 b^2 +9b^4 =98)),((2a^3 b+3ab^3 =10(2))) :} ⇔10(4a^4 +36a^2 b^2 +9b^4 )=98(2a^3 b+3ab^3 ) Put a=kb substituting into above equality then divide two sides by k^4 we get 40k^4 +360k^2 +90=196k^3 +294k ⇔20k^4 −98k^3 +180k^2 −147k+45=0 This equation has one root k=1 ⇒a=b.Replace into (2)we get 5a^4 =10⇔a=^4 (√2).Replace into (1) we have (√((√(50))+(√(48))))=^4 (√(98+40(√6))) =^4 (√([^4 (√2)((√2)+(√3))]^4 )) =^4 (√2) ((√2)+(√3)) Thus, (√((√(50))+(√(48))))=^4 (√2) ((√2)+(√3))

$$\mathrm{We}\:\mathrm{have}\:\left(\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}\right)^{\mathrm{2}} =\mathrm{98}+\mathrm{2}\sqrt{\mathrm{50}.\mathrm{48}} \\ $$$$=\mathrm{98}+\mathrm{2}\sqrt{\mathrm{25}.\mathrm{16}.\mathrm{6}}=\mathrm{98}+\mathrm{40}\sqrt{\mathrm{6}} \\ $$$$\mathrm{Hence}\:\sqrt{\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}}=\:^{\mathrm{4}} \sqrt{\left(\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}\right)^{\mathrm{2}} } \\ $$$$=\:^{\mathrm{4}} \sqrt{\mathrm{98}+\mathrm{40}\sqrt{\mathrm{6}}}=\:^{\mathrm{4}} \sqrt{\left(\mathrm{a}\sqrt{\mathrm{2}}+\mathrm{b}\sqrt{\mathrm{3}}\right)^{\mathrm{4}} }\:\left(\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{find}\:\mathrm{a},\mathrm{b}\:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{98}+\mathrm{40}\sqrt{\mathrm{6}}=\left(\mathrm{a}\sqrt{\mathrm{2}}+\mathrm{b}\sqrt{\mathrm{3}}\right)^{\mathrm{4}} \\ $$$$=\mathrm{4a}^{\mathrm{4}} +\mathrm{8a}^{\mathrm{3}} \sqrt{\mathrm{2}}.\mathrm{b}\sqrt{\mathrm{3}}+\mathrm{6}.\mathrm{2a}^{\mathrm{2}} .\mathrm{3b}^{\mathrm{2}} +\mathrm{4}.\mathrm{3b}^{\mathrm{3}} \sqrt{\mathrm{3}}.\mathrm{a}\sqrt{\mathrm{2}} \\ $$$$+\mathrm{9b}^{\mathrm{4}} =\left(\mathrm{4a}^{\mathrm{4}} +\mathrm{9b}^{\mathrm{4}} +\mathrm{36a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\left(\mathrm{8a}^{\mathrm{3}} \mathrm{b}+\mathrm{12ab}^{\mathrm{3}} \right)\sqrt{\mathrm{6}}\right. \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{4a}^{\mathrm{4}} +\mathrm{36a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{4}} =\mathrm{98}}\\{\mathrm{8a}^{\mathrm{3}} \mathrm{b}+\mathrm{12ab}^{\mathrm{3}} =\mathrm{40}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{4a}^{\mathrm{4}} +\mathrm{36a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{4}} =\mathrm{98}}\\{\mathrm{2a}^{\mathrm{3}} \mathrm{b}+\mathrm{3ab}^{\mathrm{3}} =\mathrm{10}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\Leftrightarrow\mathrm{10}\left(\mathrm{4a}^{\mathrm{4}} +\mathrm{36a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{4}} \right)=\mathrm{98}\left(\mathrm{2a}^{\mathrm{3}} \mathrm{b}+\mathrm{3ab}^{\mathrm{3}} \right) \\ $$$$\mathrm{Put}\:\mathrm{a}=\mathrm{kb}\:\mathrm{substituting}\:\mathrm{into}\:\mathrm{above} \\ $$$$\mathrm{equality}\:\mathrm{then}\:\mathrm{divide}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{by}\:\mathrm{k}^{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{40k}^{\mathrm{4}} +\mathrm{360k}^{\mathrm{2}} +\mathrm{90}=\mathrm{196k}^{\mathrm{3}} +\mathrm{294k} \\ $$$$\Leftrightarrow\mathrm{20k}^{\mathrm{4}} −\mathrm{98k}^{\mathrm{3}} +\mathrm{180k}^{\mathrm{2}} −\mathrm{147k}+\mathrm{45}=\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{one}\:\mathrm{root}\:\mathrm{k}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{b}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{5a}^{\mathrm{4}} =\mathrm{10}\Leftrightarrow\mathrm{a}=\:^{\mathrm{4}} \sqrt{\mathrm{2}}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\sqrt{\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}}=\:^{\mathrm{4}} \sqrt{\mathrm{98}+\mathrm{40}\sqrt{\mathrm{6}}} \\ $$$$=\:^{\mathrm{4}} \sqrt{\left[\:^{\mathrm{4}} \sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)\right]^{\mathrm{4}} }\:=\:^{\mathrm{4}} \sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right) \\ $$$$\:\mathrm{Thus},\:\sqrt{\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}}=\:^{\mathrm{4}} \sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right) \\ $$

Commented by Aina Samuel Temidayo last updated on 16/Sep/20

Thanks.

$$\mathrm{Thanks}. \\ $$

Answered by mr W last updated on 16/Sep/20

(√(50))+(√(48)) =(√2)(5+2(√6)) =(√2)[((√2))^2 +2(√2)(√3)+((√3))^2 ] =(√2)[(√2)+(√3)]^2 ⇒(√((√(50))+(√(48))))=(2)^(1/4) ((√2)+(√3))

$$\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}} \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right) \\ $$$$=\sqrt{\mathrm{2}}\left[\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\sqrt{\mathrm{3}}+\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right] \\ $$$$=\sqrt{\mathrm{2}}\left[\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\sqrt{\mathrm{50}}+\sqrt{\mathrm{48}}}=\sqrt[{\mathrm{4}}]{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right) \\ $$

Answered by Dwaipayan Shikari last updated on 16/Sep/20

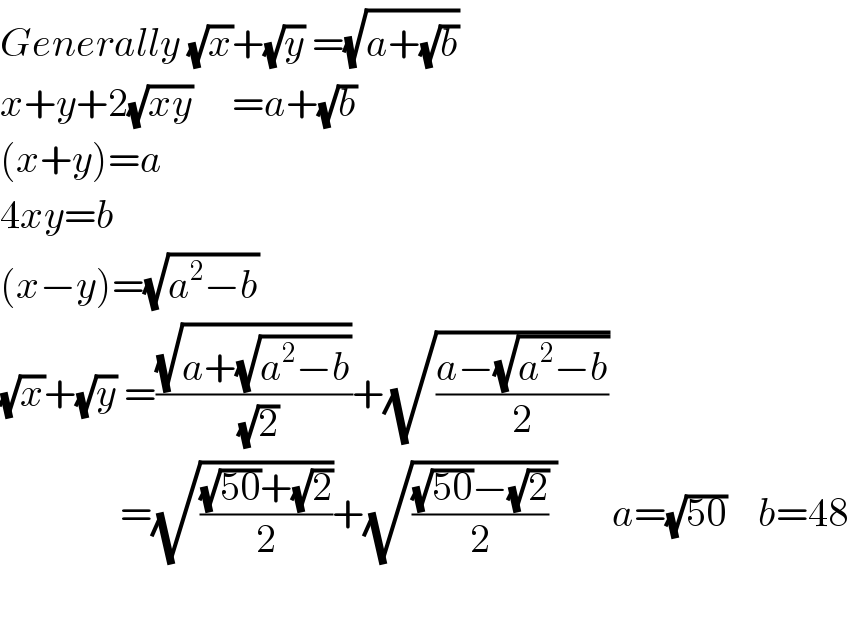
Generally (√x)+(√y) =(√(a+(√b))) x+y+2(√(xy)) =a+(√b) (x+y)=a 4xy=b (x−y)=(√(a^2 −b)) (√x)+(√y) =((√(a+(√(a^2 −b))))/( (√2)))+(√((a−(√(a^2 −b)))/2)) =(√(((√(50))+(√2))/2))+(√((((√(50))−(√2))/2) )) a=(√(50)) b=48

$${Generally}\:\sqrt{{x}}+\sqrt{{y}}\:=\sqrt{{a}+\sqrt{{b}}} \\ $$$${x}+{y}+\mathrm{2}\sqrt{{xy}}\:\:\:\:\:={a}+\sqrt{{b}} \\ $$$$\left({x}+{y}\right)={a} \\ $$$$\mathrm{4}{xy}={b} \\ $$$$\left({x}−{y}\right)=\sqrt{{a}^{\mathrm{2}} −{b}} \\ $$$$\sqrt{{x}}+\sqrt{{y}}\:=\frac{\sqrt{{a}+\sqrt{{a}^{\mathrm{2}} −{b}}}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{a}−\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\sqrt{\mathrm{50}}+\sqrt{\mathrm{2}}}{\mathrm{2}}}+\sqrt{\frac{\sqrt{\mathrm{50}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\:}\:\:\:\:\:\:\:{a}=\sqrt{\mathrm{50}}\:\:\:\:{b}=\mathrm{48} \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 16/Sep/20

(√((√(49))+(√(48)))) =(√(((√(49))+1)/2)) +(√(((√(49))−1)/2)) =2+(√3) =(√(8/2)) +(√(6/2)) (√((√(64))+(√(63)))) =(√((8+1)/2)) +(√(((8−1)/2) )) =(√(9/2))+(√(7/2)) (√((√(100))+(√(99)))) =(√(((11)/2) )) +(√(9/2)) (√((√(81))+(√(80)))) =(√((10)/2)) +(√(9/2)) Have you noticed any pattern? (√1) =(√((2/2) ))+(√(0/2)) (√((√4)+(√3))) =(√(3/2)) +(√(1/2)) (√((√9)+(√8))) =(√(4/2))+(√(2/2)) (√((√(16))+(√(15))))=(√(5/2)) +(√(3/2)) (√((√(25))+(√(24)))) =(√(6/2)) +(√(4/2)) (√((√(36))+(√(35))))=(√(7/2))+(√(5/2)) (√((√n^2 )+(√(n^2 −1)))) =(√((n+1)/2)) +(√((n−1)/2)) (√(n+(√(n^2 −1)))) =(√((n+1)/2)) +(√((n−1)/2))

$$\sqrt{\sqrt{\mathrm{49}}+\sqrt{\mathrm{48}}}\:=\sqrt{\frac{\sqrt{\mathrm{49}}+\mathrm{1}}{\mathrm{2}}}\:+\sqrt{\frac{\sqrt{\mathrm{49}}−\mathrm{1}}{\mathrm{2}}}\:=\mathrm{2}+\sqrt{\mathrm{3}}\:=\sqrt{\frac{\mathrm{8}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{6}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{64}}+\sqrt{\mathrm{63}}}\:=\sqrt{\frac{\mathrm{8}+\mathrm{1}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{8}−\mathrm{1}}{\mathrm{2}}\:}\:=\sqrt{\frac{\mathrm{9}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{100}}+\sqrt{\mathrm{99}}}\:=\sqrt{\frac{\mathrm{11}}{\mathrm{2}}\:}\:+\sqrt{\frac{\mathrm{9}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{81}}+\sqrt{\mathrm{80}}}\:\:=\sqrt{\frac{\mathrm{10}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{9}}{\mathrm{2}}} \\ $$$${Have}\:{you}\:{noticed}\:{any}\:{pattern}? \\ $$$$\sqrt{\mathrm{1}}\:=\sqrt{\frac{\mathrm{2}}{\mathrm{2}}\:}+\sqrt{\frac{\mathrm{0}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{4}}+\sqrt{\mathrm{3}}}\:\:=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{9}}+\sqrt{\mathrm{8}}}\:=\sqrt{\frac{\mathrm{4}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{2}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{16}}+\sqrt{\mathrm{15}}}=\sqrt{\frac{\mathrm{5}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{25}}+\sqrt{\mathrm{24}}}\:=\sqrt{\frac{\mathrm{6}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{4}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{\mathrm{36}}+\sqrt{\mathrm{35}}}=\sqrt{\frac{\mathrm{7}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$$\sqrt{\sqrt{{n}^{\mathrm{2}} }+\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}\:\:\:=\sqrt{\frac{{n}+\mathrm{1}}{\mathrm{2}}}\:+\sqrt{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \\ $$$$\sqrt{{n}+\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}\:=\sqrt{\frac{{n}+\mathrm{1}}{\mathrm{2}}}\:+\sqrt{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \\ $$

Commented by Rasheed.Sindhi last updated on 16/Sep/20

Actual learning from your general method! Thank you.

$$\mathcal{A}{ctual}\:{learning}\:{from}\:{your} \\ $$$${general}\:{method}!\:{Thank}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com