Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 113928 by ZiYangLee last updated on 16/Sep/20

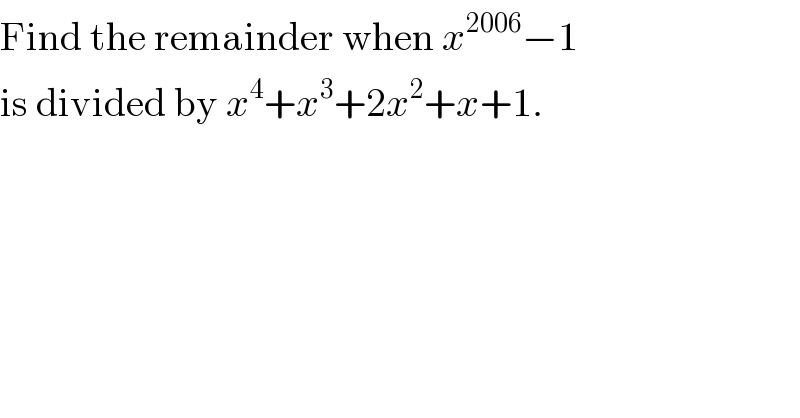
Find the remainder when x^(2006) −1 is divided by x^4 +x^3 +2x^2 +x+1.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:{x}^{\mathrm{2006}} −\mathrm{1}\: \\ $$$$\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}. \\ $$

Answered by MJS_new last updated on 16/Sep/20

x^4 +x^3 +2x^2 +x+1=(x^2 +1)(x^2 +x+1) the remaining fractions of ((x^(2n) −1)/((x^2 +1)(x^2 +x+1))) are 0 for n=6k ((x^2 −1)/((x^2 +1)(x^2 +x+1))) for n=6k+1 [2006=2(6×167+1)] −((x+2)/(x^2 +x+1)) for n=6k+2 ((2x)/(x^2 +1)) for n=6k+3 −((2x+1)/(x^2 +x+1)) for n=6k+4 ((x^3 +x−2)/((x^2 +1)(x^2 +x+1))) for n=6k+5

$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}=\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\mathrm{the}\:\mathrm{remaining}\:\mathrm{fractions}\:\mathrm{of} \\ $$$$\frac{{x}^{\mathrm{2}{n}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$$\mathrm{are} \\ $$$$\mathrm{0}\:\mathrm{for}\:{n}=\mathrm{6}{k} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{1}\:\left[\mathrm{2006}=\mathrm{2}\left(\mathrm{6}×\mathrm{167}+\mathrm{1}\right)\right] \\ $$$$−\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{2} \\ $$$$\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{3} \\ $$$$−\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{4} \\ $$$$\frac{{x}^{\mathrm{3}} +{x}−\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{5} \\ $$

Commented by 1549442205PVT last updated on 16/Sep/20

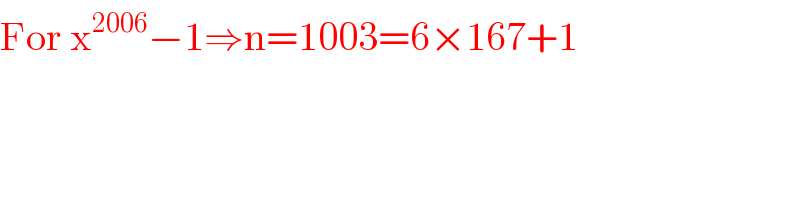
For x^(2006) −1⇒n=1003=6×167+1

$$\mathrm{For}\:\mathrm{x}^{\mathrm{2006}} −\mathrm{1}\Rightarrow\mathrm{n}=\mathrm{1003}=\mathrm{6}×\mathrm{167}+\mathrm{1} \\ $$

Commented by MJS_new last updated on 16/Sep/20

you are right, thank you

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right},\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com