Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 113929 by gloriousman last updated on 16/Sep/20

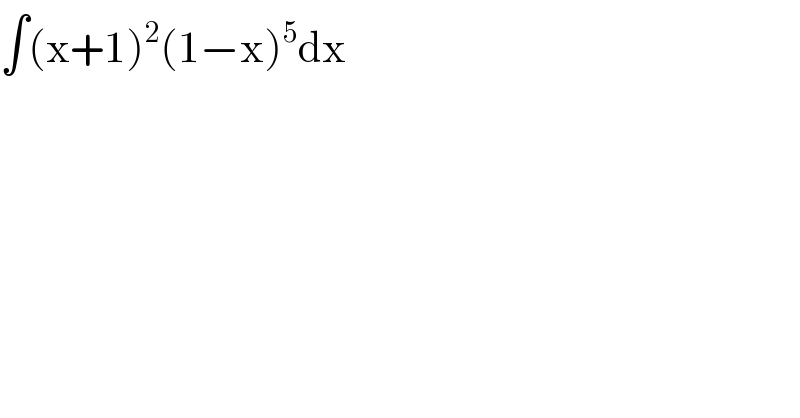
∫(x+1)^2 (1−x)^5 dx

$$\int\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{5}} \mathrm{dx}\: \\ $$$$ \\ $$

Commented by ShakaLaka last updated on 16/Sep/20

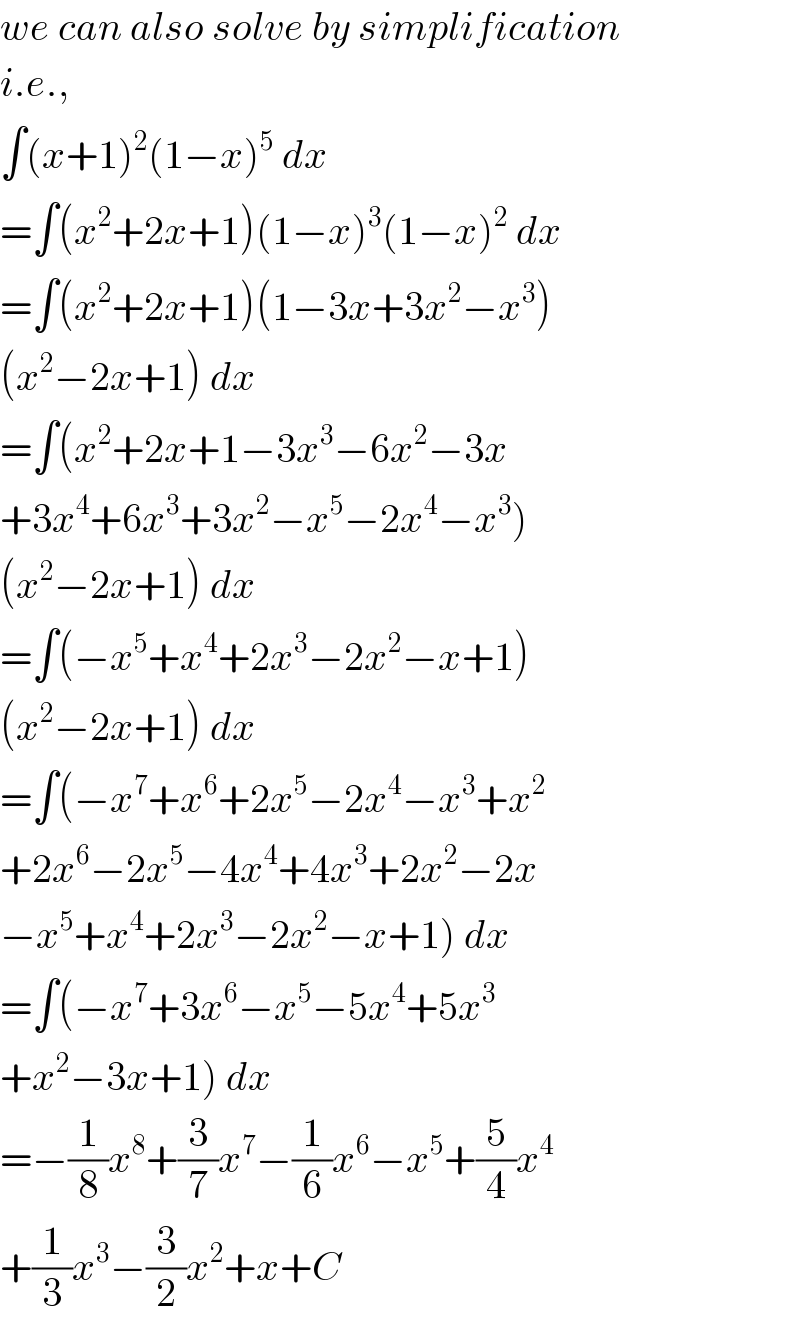
we can also solve by simplification i.e., ∫(x+1)^2 (1−x)^5 dx =∫(x^2 +2x+1)(1−x)^3 (1−x)^2 dx =∫(x^2 +2x+1)(1−3x+3x^2 −x^3 ) (x^2 −2x+1) dx =∫(x^2 +2x+1−3x^3 −6x^2 −3x +3x^4 +6x^3 +3x^2 −x^5 −2x^4 −x^3 ) (x^2 −2x+1) dx =∫(−x^5 +x^4 +2x^3 −2x^2 −x+1) (x^2 −2x+1) dx =∫(−x^7 +x^6 +2x^5 −2x^4 −x^3 +x^2 +2x^6 −2x^5 −4x^4 +4x^3 +2x^2 −2x −x^5 +x^4 +2x^3 −2x^2 −x+1) dx =∫(−x^7 +3x^6 −x^5 −5x^4 +5x^3 +x^2 −3x+1) dx =−(1/8)x^8 +(3/7)x^7 −(1/6)x^6 −x^5 +(5/4)x^4 +(1/3)x^3 −(3/2)x^2 +x+C

$${we}\:{can}\:{also}\:{solve}\:{by}\:{simplification} \\ $$$${i}.{e}., \\ $$$$\int\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{5}} \:{dx} \\ $$$$=\int\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} \:{dx} \\ $$$$=\int\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{3}{x}+\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} \right) \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)\:{dx} \\ $$$$=\int\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} −\mathrm{3}{x}\right. \\ $$$$\left.+\mathrm{3}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} \right) \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)\:{dx} \\ $$$$=\int\left(−{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)\:{dx} \\ $$$$=\int\left(−{x}^{\mathrm{7}} +{x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \right. \\ $$$$+\mathrm{2}{x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x} \\ $$$$\left.−{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:{dx} \\ $$$$=\int\left(−{x}^{\mathrm{7}} +\mathrm{3}{x}^{\mathrm{6}} −{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} \right. \\ $$$$\left.+{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}\right)\:{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{8}} +\frac{\mathrm{3}}{\mathrm{7}}{x}^{\mathrm{7}} −\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{6}} −{x}^{\mathrm{5}} +\frac{\mathrm{5}}{\mathrm{4}}{x}^{\mathrm{4}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} +{x}+{C} \\ $$

Commented by MJS_new last updated on 16/Sep/20

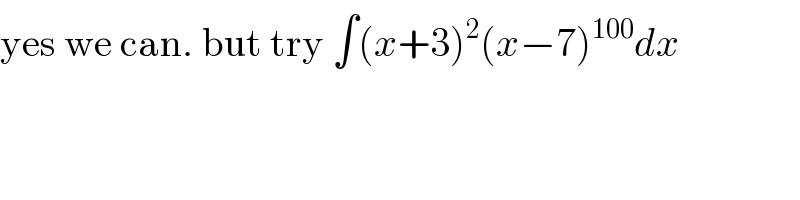
yes we can. but try ∫(x+3)^2 (x−7)^(100) dx

$$\mathrm{yes}\:\mathrm{we}\:\mathrm{can}.\:\mathrm{but}\:\mathrm{try}\:\int\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}−\mathrm{7}\right)^{\mathrm{100}} {dx} \\ $$

Commented by ShakaLaka last updated on 16/Sep/20

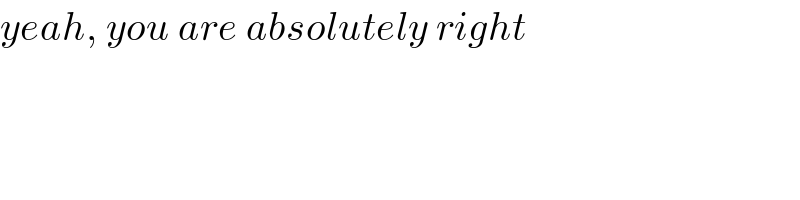
yeah, you are absolutely right

$${yeah},\:{you}\:{are}\:{absolutely}\:{right} \\ $$

Commented by mathmax by abdo last updated on 16/Sep/20

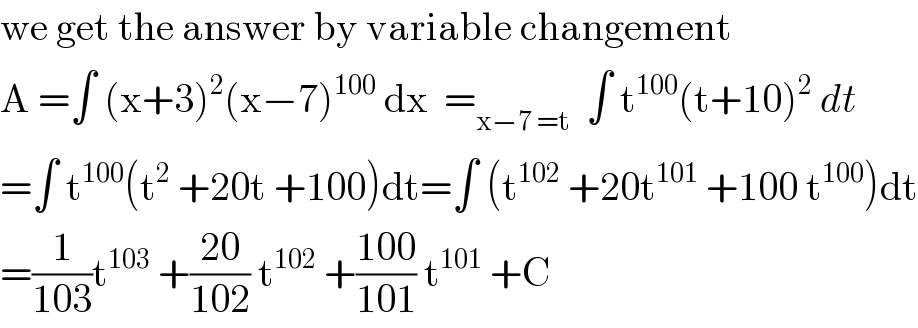
we get the answer by variable changement A =∫ (x+3)^2 (x−7)^(100) dx =_(x−7 =t) ∫ t^(100) (t+10)^2 dt =∫ t^(100) (t^2 +20t +100)dt=∫ (t^(102) +20t^(101) +100 t^(100) )dt =(1/(103))t^(103) +((20)/(102)) t^(102) +((100)/(101)) t^(101) +C

$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{by}\:\mathrm{variable}\:\mathrm{changement}\: \\ $$$$\mathrm{A}\:=\int\:\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{7}\right)^{\mathrm{100}} \:\mathrm{dx}\:\:=_{\mathrm{x}−\mathrm{7}\:=\mathrm{t}} \:\:\int\:\mathrm{t}^{\mathrm{100}} \left(\mathrm{t}+\mathrm{10}\right)^{\mathrm{2}} \:{dt} \\ $$$$=\int\:\mathrm{t}^{\mathrm{100}} \left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{20t}\:+\mathrm{100}\right)\mathrm{dt}=\int\:\left(\mathrm{t}^{\mathrm{102}} \:+\mathrm{20t}^{\mathrm{101}} \:+\mathrm{100}\:\mathrm{t}^{\mathrm{100}} \right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{103}}\mathrm{t}^{\mathrm{103}} \:+\frac{\mathrm{20}}{\mathrm{102}}\:\mathrm{t}^{\mathrm{102}} \:+\frac{\mathrm{100}}{\mathrm{101}}\:\mathrm{t}^{\mathrm{101}} \:+\mathrm{C} \\ $$

Answered by MJS_new last updated on 16/Sep/20

∫(x+1)^2 (1−x)^5 dx= [t=1−x → dx=dt] =∫t^5 (t−2)^2 dt=∫t^7 −4t^6 +4t^5 dt= =(1/8)t^8 −(4/7)t^7 +(2/3)t^6 =((t^6 (21t^2 −96t+112))/(168))= =(((1−x)^6 (21x^2 +54x+37))/(168))+C

$$\int\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{5}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{1}−{x}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int{t}^{\mathrm{5}} \left({t}−\mathrm{2}\right)^{\mathrm{2}} {dt}=\int{t}^{\mathrm{7}} −\mathrm{4}{t}^{\mathrm{6}} +\mathrm{4}{t}^{\mathrm{5}} {dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}{t}^{\mathrm{8}} −\frac{\mathrm{4}}{\mathrm{7}}{t}^{\mathrm{7}} +\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{6}} =\frac{{t}^{\mathrm{6}} \left(\mathrm{21}{t}^{\mathrm{2}} −\mathrm{96}{t}+\mathrm{112}\right)}{\mathrm{168}}= \\ $$$$=\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{6}} \left(\mathrm{21}{x}^{\mathrm{2}} +\mathrm{54}{x}+\mathrm{37}\right)}{\mathrm{168}}+{C} \\ $$

Answered by 1549442205PVT last updated on 16/Sep/20

(x+1)^2 (1−x)^5 =[(1−x)(1+x)]^2 (1−x)^3 =(1−x^2 )^2 (1−x)^3 =(x^4 −2x^2 +1)(1−3x+3x^2 −x^3 ) =x^4 −2x^2 +1−3x^5 +6x^3 −3x+3x^6 −6x^4 +3x^2 −x^7 +2x^5 −x^3 =−x^7 +3x^6 −x^5 −5x^4 +5x^3 +x^2 −3x+1 Hence,∫(x+1)^2 (1−x)^5 dx =∫(−x^7 +3x^6 −x^5 −5x^4 +5x^3 +x^2 −3x+1)dx =((−x^8 )/8)+((3x^7 )/7)−(x^6 /6)−x^5 +((5x^4 )/4)+(x^3 /3)−((3x^2 )/2)+x+C

$$\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{5}} =\left[\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)\right]^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} =\left(\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}−\mathrm{3x}+\mathrm{3x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} \right) \\ $$$$=\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{3x}^{\mathrm{5}} +\mathrm{6x}^{\mathrm{3}} −\mathrm{3x}+\mathrm{3x}^{\mathrm{6}} −\mathrm{6x}^{\mathrm{4}} \\ $$$$+\mathrm{3x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{7}} +\mathrm{2x}^{\mathrm{5}} −\mathrm{x}^{\mathrm{3}} \\ $$$$=−\mathrm{x}^{\mathrm{7}} +\mathrm{3x}^{\mathrm{6}} −\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} +\mathrm{5x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1} \\ $$$$\mathrm{Hence},\int\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{5}} \mathrm{dx} \\ $$$$=\int\left(−\mathrm{x}^{\mathrm{7}} +\mathrm{3x}^{\mathrm{6}} −\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} +\mathrm{5x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\right)\mathrm{dx} \\ $$$$=\frac{−\boldsymbol{\mathrm{x}}^{\mathrm{8}} }{\mathrm{8}}+\frac{\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{7}} }{\mathrm{7}}−\frac{\boldsymbol{\mathrm{x}}^{\mathrm{6}} }{\mathrm{6}}−\boldsymbol{\mathrm{x}}^{\mathrm{5}} +\frac{\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{4}} }{\mathrm{4}}+\frac{\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}+\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{C}} \\ $$

Commented by MJS_new last updated on 16/Sep/20

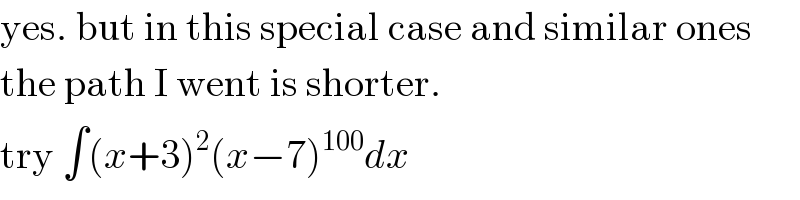
yes. but in this special case and similar ones the path I went is shorter. try ∫(x+3)^2 (x−7)^(100) dx

$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{in}\:\mathrm{this}\:\mathrm{special}\:\mathrm{case}\:\mathrm{and}\:\mathrm{similar}\:\mathrm{ones} \\ $$$$\mathrm{the}\:\mathrm{path}\:\mathrm{I}\:\mathrm{went}\:\mathrm{is}\:\mathrm{shorter}. \\ $$$$\mathrm{try}\:\int\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}−\mathrm{7}\right)^{\mathrm{100}} {dx} \\ $$

Commented by 1549442205PVT last updated on 16/Sep/20

Thank Sir.

$$\mathrm{Thank}\:\mathrm{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com