Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 113952 by bemath last updated on 16/Sep/20

find all asymptotes of function f(x)=(((x^2 +4x−5)/(x^2 +x+3)))^(x+5)

$${find}\:{all}\:{asymptotes}\:{of}\:{function} \\ $$$${f}\left({x}\right)=\left(\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right)^{{x}+\mathrm{5}} \\ $$

Commented by MJS_new last updated on 16/Sep/20

forgot the squares???

$$\mathrm{forgot}\:\mathrm{the}\:\mathrm{squares}??? \\ $$

Commented by bemath last updated on 16/Sep/20

yes sir. sorry

$${yes}\:{sir}.\:{sorry} \\ $$

Commented by MJS_new last updated on 16/Sep/20

if it′s f(x)=(((x^2 +4x−5)/(x^2 +x+3)))^(x+5) I get lim_(x→±∞) f(x) =e^3 ⇒ horizontal asymptote y=e^3 for the rest I′m not sure as we still get some real solutions for ((x^2 +4x−5)/(x^2 +x+3))<0

$$\mathrm{if}\:\mathrm{it}'\mathrm{s} \\ $$$${f}\left({x}\right)=\left(\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right)^{{x}+\mathrm{5}} \\ $$$$\mathrm{I}\:\mathrm{get}\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}{f}\left({x}\right)\:=\mathrm{e}^{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{horizontal}\:\mathrm{asymptote}\:{y}=\mathrm{e}^{\mathrm{3}} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{as}\:\mathrm{we}\:\mathrm{still}\:\mathrm{get}\:\mathrm{some} \\ $$$$\mathrm{real}\:\mathrm{solutions}\:\mathrm{for}\:\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}<\mathrm{0} \\ $$

Commented by MJS_new last updated on 16/Sep/20

...there is a vertical asymptote x=−5

$$...\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{vertical}\:\mathrm{asymptote}\:{x}=−\mathrm{5} \\ $$

Answered by 1549442205PVT last updated on 16/Sep/20

we find horizontal asymptote: y=limf(x)_(x→∞) =lim_(x→∞) (1+((3x−8)/(x^2 +x+3)))^(x+5) =lim_(x→∞) (1+(1/((x^2 +x+3)/(3x−8))))((x^2 +x+3)/(3x−8)).((((3x−8)(x+5))/(x^2 +x+3))) =e^(lim_(x→∞) ((3x^2 +7x−40)/(x^2 +x+3))) =e^(lim_(x→∞) (3+((4x−49)/(x^2 +x+3)))) =e^(3 ) since lim_(x→∞) (3+((4x−49)/(x^2 +x+3)))=3 Therefore graph of function f(x)=(((x^2 +4x−5)/(x^2 +x+3)))^(x+5) has the horizontal asymptote y=e^3

$$\mathrm{we}\:\mathrm{find}\:\mathrm{horizontal}\:\mathrm{asymptote}: \\ $$$$\mathrm{y}=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{limf}\left(\mathrm{x}\right)}=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{3x}−\mathrm{8}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}\right)^{\mathrm{x}+\mathrm{5}} \\ $$$$=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}{\mathrm{3x}−\mathrm{8}}}\right)\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}{\mathrm{3x}−\mathrm{8}}.\left(\frac{\left(\mathrm{3x}−\mathrm{8}\right)\left(\mathrm{x}+\mathrm{5}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}\right) \\ $$$$=\mathrm{e}^{\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{7x}−\mathrm{40}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}} =\mathrm{e}^{\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{3}+\frac{\mathrm{4x}−\mathrm{49}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}\right)} \\ $$$$=\mathrm{e}^{\mathrm{3}\:} \mathrm{since}\:\:\:\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{3}+\frac{\mathrm{4x}−\mathrm{49}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}}\right)=\mathrm{3} \\ $$$$\mathrm{Therefore}\:\mathrm{graph}\:\mathrm{of}\:\mathrm{function} \\ $$$${f}\left({x}\right)=\left(\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right)^{{x}+\mathrm{5}} \mathrm{has}\:\mathrm{the} \\ $$$$\mathrm{horizontal}\:\mathrm{asymptote}\:\mathrm{y}=\mathrm{e}^{\mathrm{3}} \\ $$

Answered by bobhans last updated on 16/Sep/20

(1) horizontal asymptotes y = lim_(x→±∞) f(x) = lim_(x→±∞) (((x^2 +4x−5)/(x^2 +x+3)))^(x+5) = e^(lim_(x→±∞) (((x^2 +4x−5)/(x^2 +x+3)) − 1).(x+5)) = e^(lim_(x→±∞) ((((3x−8)(x+5))/(x^2 +x+3)))) = e^3 (2)vertical asymptotes lim_(x→a) f(x)=±∞ . we aplly formula If f(x) = (((h(x))/(g(x))))^(u(x)) ; vertical asymptotes we get from h(x)=0 , in this case h(x)=x^2 +4x−5=(x+5)(x−1)=0 so the vertical asymptotes is x=−5 ∧x=1

$$\left(\mathrm{1}\right)\:{horizontal}\:{asymptotes}\: \\ $$$$\:{y}\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right)^{{x}+\mathrm{5}} \\ $$$$\:\:\:=\:{e}^{\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\:−\:\mathrm{1}\right).\left({x}+\mathrm{5}\right)} \\ $$$$\:\:\:=\:{e}^{\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\left(\frac{\left(\mathrm{3}{x}−\mathrm{8}\right)\left({x}+\mathrm{5}\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right)} \:=\:{e}^{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right){vertical}\:{asymptotes}\: \\ $$$$\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{f}\left({x}\right)=\pm\infty\:.\:{we}\:{aplly}\:{formula} \\ $$$$\:{If}\:{f}\left({x}\right)\:=\:\left(\frac{{h}\left({x}\right)}{{g}\left({x}\right)}\right)^{{u}\left({x}\right)} ;\:{vertical}\:{asymptotes} \\ $$$${we}\:{get}\:{from}\:{h}\left({x}\right)=\mathrm{0}\:,\:{in}\:{this}\:{case} \\ $$$${h}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{5}=\left({x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${so}\:{the}\:{vertical}\:{asymptotes}\:{is}\:{x}=−\mathrm{5}\:\wedge{x}=\mathrm{1} \\ $$

Commented by MJS_new last updated on 16/Sep/20

but f(1)=0 is defined, so there′s no asymptote

$$\mathrm{but}\:{f}\left(\mathrm{1}\right)=\mathrm{0}\:\mathrm{is}\:\mathrm{defined},\:\mathrm{so}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{asymptote} \\ $$

Commented by bobhans last updated on 16/Sep/20

how about f(−5) sir? oo f(−5) = 0^0 sir. yes x=−5 is vertical asymptotes

$${how}\:{about}\:{f}\left(−\mathrm{5}\right)\:{sir}?\: \\ $$$${oo}\:{f}\left(−\mathrm{5}\right)\:=\:\mathrm{0}^{\mathrm{0}} \:{sir}.\:{yes}\:{x}=−\mathrm{5}\:{is} \\ $$$${vertical}\:{asymptotes} \\ $$

Commented by bobhans last updated on 16/Sep/20

Commented by bobhans last updated on 16/Sep/20

i apply geogebra. this graph

$${i}\:{apply}\:{geogebra}.\:{this}\:{graph}\: \\ $$

Commented by MJS_new last updated on 16/Sep/20

f(−5)=((0/(17)))^0 =0^0 which is not defined many graphic calculators use 0^0 =1 and in this case lim_(x→−5) f(x) =1 ⇒ different situation from f(1)=0 we would also not say y=x^2 has an asymptote y=0, would we?

$${f}\left(−\mathrm{5}\right)=\left(\frac{\mathrm{0}}{\mathrm{17}}\right)^{\mathrm{0}} =\mathrm{0}^{\mathrm{0}} \:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\mathrm{many}\:\mathrm{graphic}\:\mathrm{calculators}\:\mathrm{use}\:\mathrm{0}^{\mathrm{0}} =\mathrm{1}\:\mathrm{and}\:\mathrm{in} \\ $$$$\mathrm{this}\:\mathrm{case}\:\underset{{x}\rightarrow−\mathrm{5}} {\mathrm{lim}}\:{f}\left({x}\right)\:=\mathrm{1}\:\Rightarrow\:\mathrm{different}\:\mathrm{situation} \\ $$$$\mathrm{from}\:{f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{would}\:\mathrm{also}\:\mathrm{not}\:\mathrm{say}\:{y}={x}^{\mathrm{2}} \:\mathrm{has}\:\mathrm{an}\:\mathrm{asymptote} \\ $$$${y}=\mathrm{0},\:\mathrm{would}\:\mathrm{we}? \\ $$

Commented by bemath last updated on 16/Sep/20

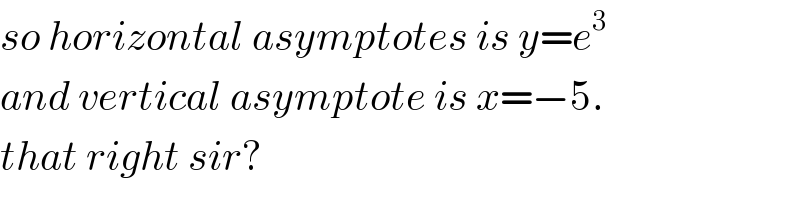
so horizontal asymptotes is y=e^3 and vertical asymptote is x=−5. that right sir?

$${so}\:{horizontal}\:{asymptotes}\:{is}\:{y}={e}^{\mathrm{3}} \\ $$$${and}\:{vertical}\:{asymptote}\:{is}\:{x}=−\mathrm{5}. \\ $$$${that}\:{right}\:{sir}? \\ $$

Commented by MJS_new last updated on 16/Sep/20

yes in my opinion.

$$\mathrm{yes}\:\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}. \\ $$

Commented by bemath last updated on 16/Sep/20

thank you sir. i agree

$${thank}\:{you}\:{sir}.\:{i}\:{agree} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com