Question Number 114037 by mohammad17 last updated on 16/Sep/20

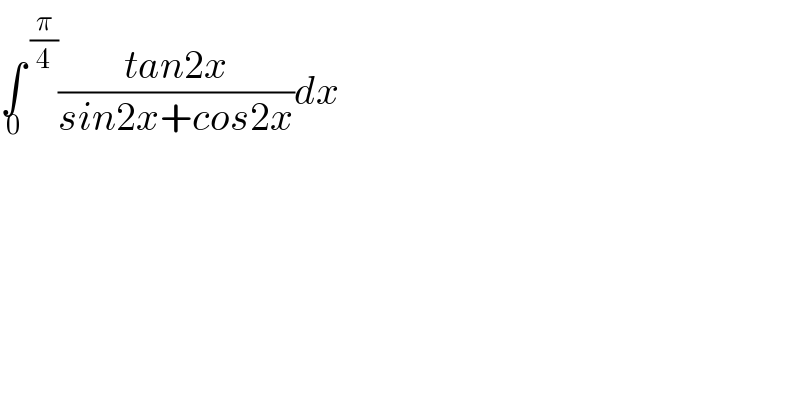
∫^( (π/4)) _0 ((tan2x)/(sin2x+cos2x))dx

Answered by Dwaipayan Shikari last updated on 16/Sep/20

∫_0 ^(π/4) ((sin2x)/(cos2x(sin2x+cos2x)))dx ∫_0 ^(π/4) (1/(cos2x))−(1/(sin2x+cos2x))dx =∫_0 ^(π/4) sec2x−(1/( (√2)))∫_0 ^(π/4) (1/( cos((π/4)−2x)))dx =(1/2)[log(sec2x+tan2x)]_0 ^(π/4) −(1/( (√2)))∫_0 ^(π/4) sec((π/4)−2x)dx →∞ Divergent

Answered by mathmax by abdo last updated on 16/Sep/20

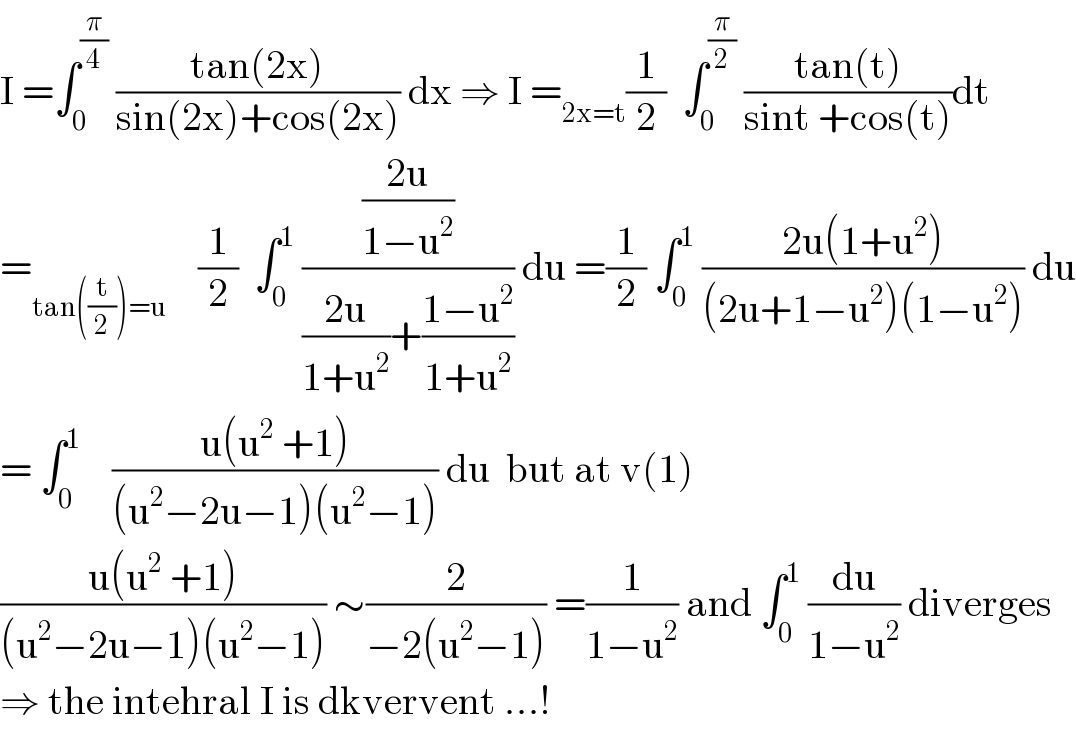
I =∫_0 ^(π/4) ((tan(2x))/(sin(2x)+cos(2x))) dx ⇒ I =_(2x=t) (1/2) ∫_0 ^(π/2) ((tan(t))/(sint +cos(t)))dt =_(tan((t/2))=u) (1/2) ∫_0 ^1 (((2u)/(1−u^2 ))/(((2u)/(1+u^2 ))+((1−u^2 )/(1+u^2 )))) du =(1/2) ∫_0 ^1 ((2u(1+u^2 ))/((2u+1−u^2 )(1−u^2 ))) du = ∫_0 ^1 ((u(u^2 +1))/((u^2 −2u−1)(u^2 −1))) du but at v(1) ((u(u^2 +1))/((u^2 −2u−1)(u^2 −1))) ∼(2/(−2(u^2 −1))) =(1/(1−u^2 )) and ∫_0 ^1 (du/(1−u^2 )) diverges ⇒ the intehral I is dkvervent ...!