
Question Number 114044 by Her_Majesty last updated on 16/Sep/20
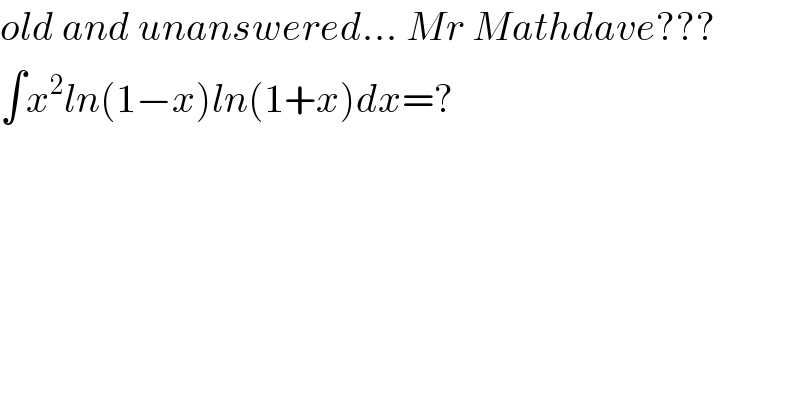
$${old}\:{and}\:{unanswered}...\:{Mr}\:{Mathdave}??? \\ $$$$\int{x}^{\mathrm{2}} {ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}+{x}\right){dx}=? \\ $$
Answered by mathdave last updated on 17/Sep/20
![sokution put x=(2y−1) (wat i did here is logical) I=∫_0 ^1 (2y−1)^2 ln(2−2y)ln(2y)dy I=ln^2 (2)∫_0 ^1 (2y−1)^2 dy+ln2∫_0 ^1 (2y−1)^2 lnydy+ln2∫_0 ^1 (2y−1)^2 ln(1−y)dy+∫_0 ^1 (2y−1)^2 lnyln(1−y)dy let I_1 =ln^2 (2)∫_0 ^1 (2y−1)^2 dy=((ln^2 (2))/3).....(1) I_2 =ln2∫_0 ^1 (2y−1)^2 lnydy+ln2∫_0 ^1 (2y−1)^2 ln(1−y)dy I_2 =2ln2∫_0 ^1 (2y−1)^2 lnydy (∂/∂a)∣_(a=1) I_2 =2ln2∫_0 ^1 (2y−1)y^(a−1) dy (∂/∂a)∣_(a=1) I_2 =((2ln2•4)/((2+a))),I_2 =−((8ln2)/9).......(2) I_3 =∫_0 ^1 (2y−1)^2 ln(1−y)lnydy but (2y−1)^2 =4y^2 −4y+1 I_3 =4∫_0 ^1 y^2 ln(1−y)lnydy−4∫_0 ^1 yln(1−y)lnydy+∫_0 ^1 ln(1−y)lnydy I_3 =(∂/∂a)∣_(a=1) −4Σ_(n=1) ^∞ (1/n)∫_0 ^1 y^n .y^2 .y^(a−1) dy+(∂/∂a)∣_(a=1) Σ_(n=1) ^∞ (1/n)∫_0 ^1 y^n .y.y^(a−1) dy+(∂/∂a)∣_(a=1) Σ_(n=1) ^∞ (1/n)∫_0 ^1 y^n .y^(a−1) dy I_3 =(∂/∂a)∣_(a=1) [−4Σ_(n=1) ^∞ (1/(n(n+2+a)))+4Σ_(n=1) ^∞ (1/(n(n+1+a)))−Σ_(n=1) ^∞ (1/(n(n+a)))] I_3 =4Σ_(n=1) ^∞ (1/(n(n+3)^2 ))−4Σ_(n=1) ^∞ (1/(n(n+2)^2 ))+Σ_(n=1) ^∞ (1/(n(n+1)^2 )) I_3 =4[Σ_(n=1) ^∞ ((1/(9n))−(1/(9(n+3)))−(1/(3(n+3)^2 )))]−4[Σ_(n=1) ^∞ ((1/(4n))−(1/(4(n+2)))−(1/(2(n+2)^2 )))]+Σ_(n=1) ^∞ ((1/n)−(1/((n+1)^2 ))−(1/((n+1)))) I_3 =((71)/(27))−((4π^2 )/(18))+(π^2 /3)−4+2−(π^2 /6)=(((17)/(27))−(π^2 /(18))).....(3) but I=I_1 +I_2 +I_3 I=((ln^2 (2))/3)−((8ln2)/9)−(π^2 /(18))+((17)/(27)) ∵∫_0 ^1 x^2 ln(1−x)ln(1+x)dx=((ln^2 (2))/3)−((8ln2)/9)−(π^2 /(18))+((17)/(27)) mathdave (i try to compressed d work and skip some steps) any complain about the working is allow](Q114050.png)
$${sokution} \\ $$$${put}\:{x}=\left(\mathrm{2}{y}−\mathrm{1}\right)\:\:\left({wat}\:{i}\:{did}\:{here}\:{is}\:{logical}\right) \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{2}−\mathrm{2}{y}\right)\mathrm{ln}\left(\mathrm{2}{y}\right){dy} \\ $$$${I}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} {dy}+\mathrm{ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}{ydy}+\mathrm{ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−{y}\right){dy}+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}{y}\mathrm{ln}\left(\mathrm{1}−{y}\right){dy} \\ $$$${let}\:{I}_{\mathrm{1}} =\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} {dy}=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3}}.....\left(\mathrm{1}\right) \\ $$$${I}_{\mathrm{2}} =\mathrm{ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}{ydy}+\mathrm{ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−{y}\right){dy} \\ $$$${I}_{\mathrm{2}} =\mathrm{2ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}{ydy} \\ $$$$\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} {I}_{\mathrm{2}} =\mathrm{2ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right){y}^{{a}−\mathrm{1}} {dy} \\ $$$$\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} {I}_{\mathrm{2}} =\frac{\mathrm{2ln2}\bullet\mathrm{4}}{\left(\mathrm{2}+{a}\right)},{I}_{\mathrm{2}} =−\frac{\mathrm{8ln2}}{\mathrm{9}}.......\left(\mathrm{2}\right) \\ $$$${I}_{\mathrm{3}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−{y}\right)\mathrm{ln}{ydy} \\ $$$${but}\:\left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{1} \\ $$$${I}_{\mathrm{3}} =\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−{y}\right)\mathrm{ln}{ydy}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {y}\mathrm{ln}\left(\mathrm{1}−{y}\right)\mathrm{ln}{ydy}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−{y}\right)\mathrm{ln}{ydy} \\ $$$${I}_{\mathrm{3}} =\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} −\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{n}} .{y}^{\mathrm{2}} .{y}^{{a}−\mathrm{1}} {dy}+\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{n}} .{y}.{y}^{{a}−\mathrm{1}} {dy}+\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{n}} .{y}^{{a}−\mathrm{1}} {dy} \\ $$$${I}_{\mathrm{3}} =\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left[−\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}+{a}\right)}+\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}+{a}\right)}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+{a}\right)}\right] \\ $$$${I}_{\mathrm{3}} =\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} }−\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}_{\mathrm{3}} =\mathrm{4}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{9}{n}}−\frac{\mathrm{1}}{\mathrm{9}\left({n}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{3}\left({n}+\mathrm{3}\right)^{\mathrm{2}} }\right)\right]−\mathrm{4}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{4}{n}}−\frac{\mathrm{1}}{\mathrm{4}\left({n}+\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{2}\right)^{\mathrm{2}} }\right)\right]+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\right) \\ $$$${I}_{\mathrm{3}} =\frac{\mathrm{71}}{\mathrm{27}}−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{4}+\mathrm{2}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\left(\frac{\mathrm{17}}{\mathrm{27}}−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\right).....\left(\mathrm{3}\right) \\ $$$${but}\:{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$${I}=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3}}−\frac{\mathrm{8ln2}}{\mathrm{9}}−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{17}}{\mathrm{27}} \\ $$$$\because\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}−{x}\right)\mathrm{ln}\left(\mathrm{1}+{x}\right){dx}=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3}}−\frac{\mathrm{8ln2}}{\mathrm{9}}−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{17}}{\mathrm{27}} \\ $$$${mathdave}\:\:\:\:\:\left({i}\:{try}\:{to}\:{compressed}\:{d}\:{work}\:{and}\:{skip}\:{some}\:{steps}\right) \\ $$$${any}\:{complain}\:{about}\:{the}\:{working}\:{is} \\ $$$${allow} \\ $$
Commented by mnjuly1970 last updated on 17/Sep/20
$${nice}\:{very}\:{nice}\:{mr}\:{dave} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
