Math Question and Answers


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 114099 by mnjuly1970 last updated on 17/Sep/20

$. . . . m a t h e m a t i c a l a n a l y s i s . . . .$ $p r o v e t h a t ::$ $\underset{n = 1}{\sum^{\infty}} (\frac{3^{n} - 1}{4^{n}}) ζ (n + 1) = π$ $You can't use 'macro parameter character #' in math mode$
	Answered by maths mind last updated on 17/Sep/20
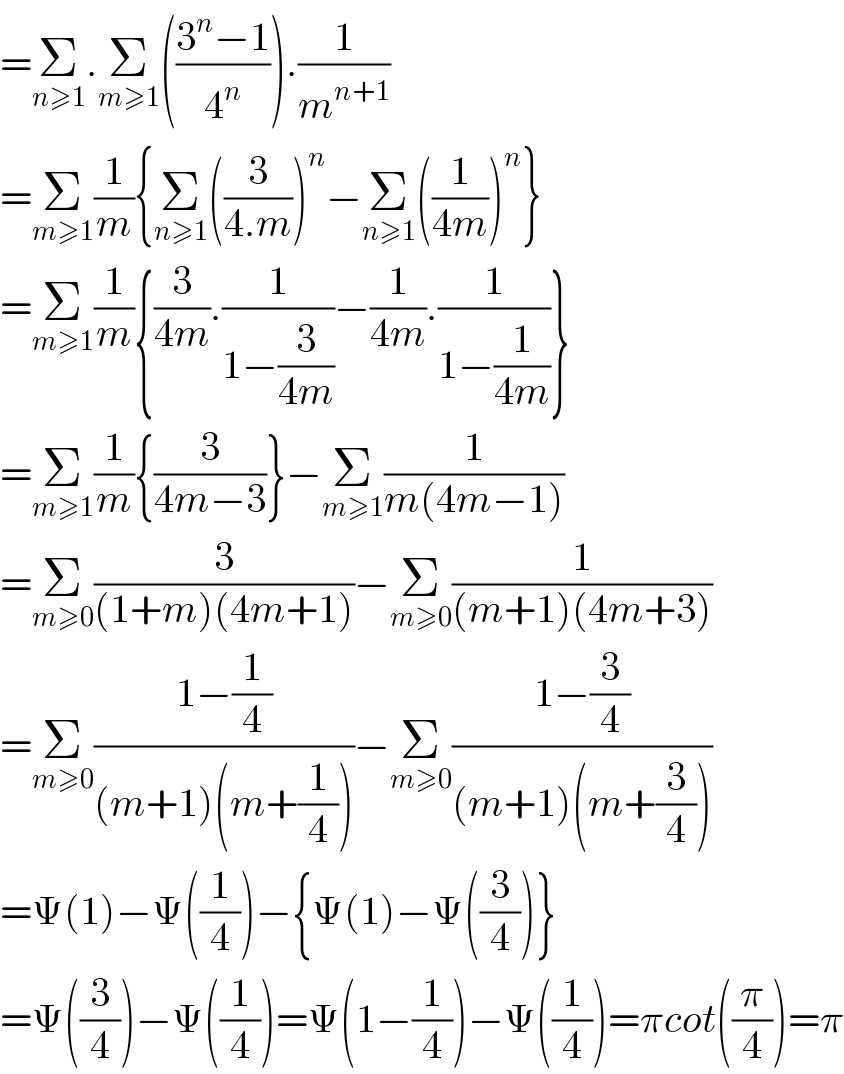
	$=Σ_(n≥1) .Σ_(m≥1) (((3^n −1)/4^n )).(1/m^(n+1) ) =Σ_(m≥1) (1/m){Σ_(n≥1) ((3/(4.m)))^n −Σ_(n≥1) ((1/(4m)))^n } =Σ_(m≥1) (1/m){(3/(4m)).(1/(1−(3/(4m))))−(1/(4m)).(1/(1−(1/(4m))))} =Σ_(m≥1) (1/m){(3/(4m−3))}−Σ_(m≥1) (1/(m(4m−1))) =Σ_(m≥0) (3/((1+m)(4m+1)))−Σ_(m≥0) (1/((m+1)(4m+3))) =Σ_(m≥0) ((1−(1/4))/((m+1)(m+(1/4))))−Σ_(m≥0) ((1−(3/4))/((m+1)(m+(3/4)))) =Ψ(1)−Ψ((1/4))−{Ψ(1)−Ψ((3/4))} =Ψ((3/4))−Ψ((1/4))=Ψ(1−(1/4))−Ψ((1/4))=πcot((π/4))=π$
	$= \sum_{n ⩾ 1} . \sum_{m ⩾ 1} (\frac{3^{n} - 1}{4^{n}}) . \frac{1}{m^{n + 1}}$ $= \sum_{m ⩾ 1} \frac{1}{m} {\sum_{n ⩾ 1} {(\frac{3}{4 . m})}^{n} - \sum_{n ⩾ 1} {(\frac{1}{4 m})}^{n}}$ $= \sum_{m ⩾ 1} \frac{1}{m} {\frac{3}{4 m} . \frac{1}{1 - \frac{3}{4 m}} - \frac{1}{4 m} . \frac{1}{1 - \frac{1}{4 m}}}$ $= \sum_{m ⩾ 1} \frac{1}{m} {\frac{3}{4 m - 3}} - \sum_{m ⩾ 1} \frac{1}{m (4 m - 1)}$ $= \sum_{m ⩾ 0} \frac{3}{(1 + m) (4 m + 1)} - \sum_{m ⩾ 0} \frac{1}{(m + 1) (4 m + 3)}$ $= \sum_{m ⩾ 0} \frac{1 - \frac{1}{4}}{(m + 1) (m + \frac{1}{4})} - \sum_{m ⩾ 0} \frac{1 - \frac{3}{4}}{(m + 1) (m + \frac{3}{4})}$ $= Ψ (1) - Ψ (\frac{1}{4}) - {Ψ (1) - Ψ (\frac{3}{4})}$ $= Ψ (\frac{3}{4}) - Ψ (\frac{1}{4}) = Ψ (1 - \frac{1}{4}) - Ψ (\frac{1}{4}) = π c o t (\frac{π}{4}) = π$
	Commented by mnjuly1970 last updated on 18/Sep/20

	$t h a n k y o u s i r . g r a t e f u l . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum