Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 114110 by bemath last updated on 17/Sep/20

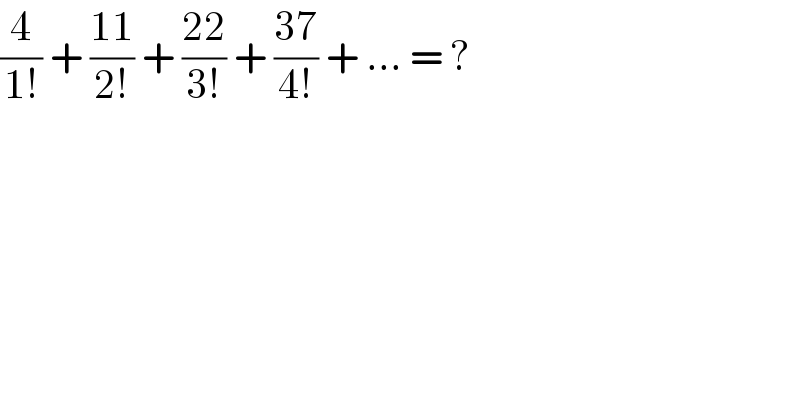
(4/(1!)) + ((11)/(2!)) + ((22)/(3!)) + ((37)/(4!)) + ... = ?

$$\frac{\mathrm{4}}{\mathrm{1}!}\:+\:\frac{\mathrm{11}}{\mathrm{2}!}\:+\:\frac{\mathrm{22}}{\mathrm{3}!}\:+\:\frac{\mathrm{37}}{\mathrm{4}!}\:+\:...\:=\:? \\ $$

Commented by Dwaipayan Shikari last updated on 17/Sep/20

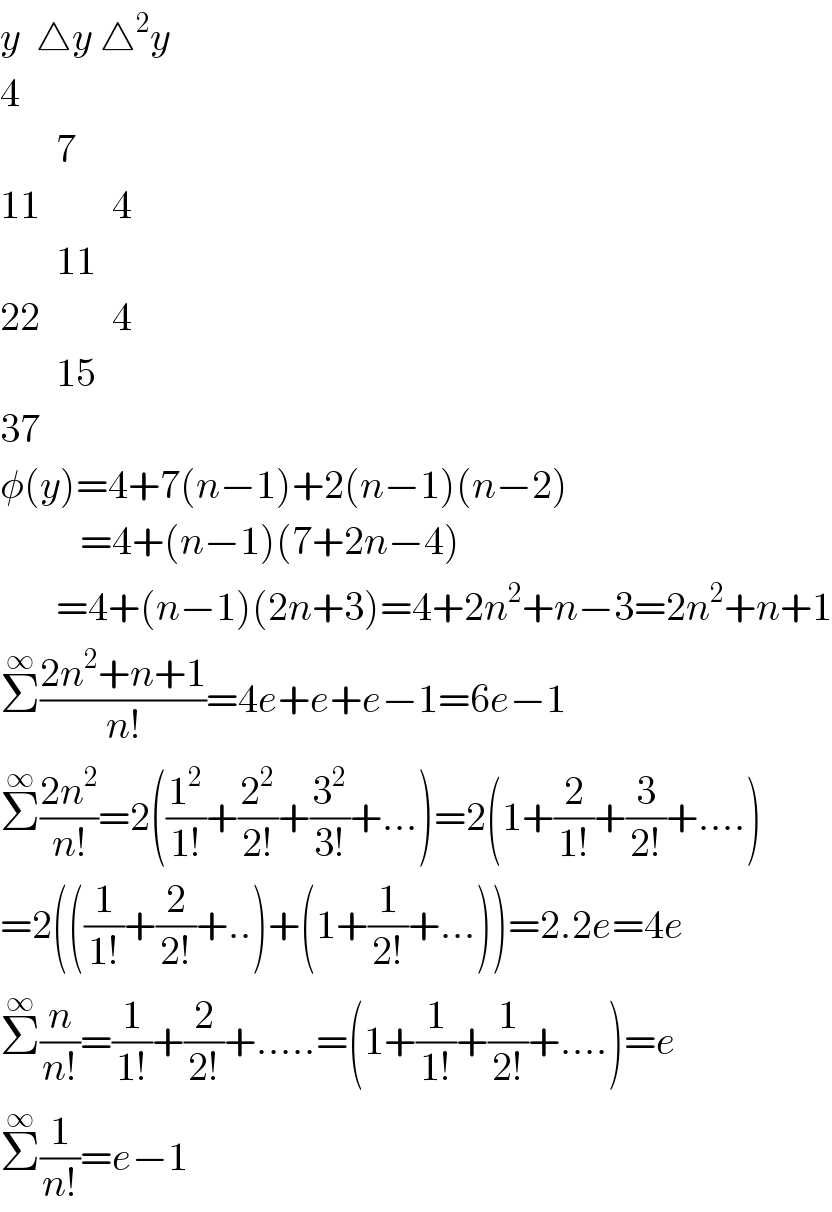
y △y △^2 y 4 7 11 4 11 22 4 15 37 φ(y)=4+7(n−1)+2(n−1)(n−2) =4+(n−1)(7+2n−4) =4+(n−1)(2n+3)=4+2n^2 +n−3=2n^2 +n+1 Σ^∞ ((2n^2 +n+1)/(n!))=4e+e+e−1=6e−1 Σ^∞ ((2n^2 )/(n!))=2((1^2 /(1!))+(2^2 /(2!))+(3^2 /(3!))+...)=2(1+(2/(1!))+(3/(2!))+....) =2(((1/(1!))+(2/(2!))+..)+(1+(1/(2!))+...))=2.2e=4e Σ^∞ (n/(n!))=(1/(1!))+(2/(2!))+.....=(1+(1/(1!))+(1/(2!))+....)=e Σ^∞ (1/(n!))=e−1

$${y}\:\:\bigtriangleup{y}\:\bigtriangleup^{\mathrm{2}} {y} \\ $$$$\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{7} \\ $$$$\mathrm{11}\:\:\:\:\:\:\:\:\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{11} \\ $$$$\mathrm{22}\:\:\:\:\:\:\:\:\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{15} \\ $$$$\mathrm{37} \\ $$$$\phi\left({y}\right)=\mathrm{4}+\mathrm{7}\left({n}−\mathrm{1}\right)+\mathrm{2}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{4}+\left({n}−\mathrm{1}\right)\left(\mathrm{7}+\mathrm{2}{n}−\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{4}+\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)=\mathrm{4}+\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{3}=\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{1} \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{1}}{{n}!}=\mathrm{4}{e}+{e}+{e}−\mathrm{1}=\mathrm{6}{e}−\mathrm{1} \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{2}{n}^{\mathrm{2}} }{{n}!}=\mathrm{2}\left(\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}!}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{3}!}+...\right)=\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+....\right) \\ $$$$=\mathrm{2}\left(\left(\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{2}!}+..\right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}!}+...\right)\right)=\mathrm{2}.\mathrm{2}{e}=\mathrm{4}{e} \\ $$$$\overset{\infty} {\sum}\frac{{n}}{{n}!}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{2}!}+.....=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+....\right)={e} \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{1}}{{n}!}={e}−\mathrm{1} \\ $$

Commented by bemath last updated on 17/Sep/20

bravoo

$${bravoo} \\ $$

Answered by bobhans last updated on 17/Sep/20

S = Σ_(n=1) ^∞ ((2n^2 +n+1)/(n!))=Σ_(n=1) ^∞ ((2n(n−1)+3n+1)/(n!)) = Σ_(n=1) ^∞ ((2n(n−1))/(n!))+Σ_(n=1) ^∞ ((3n)/(n!)) + Σ_(n=1) ^∞ (1/(n!)) S_1 =Σ_(n=1) ^∞ (1/(n!))=e−1. [ e^x =Σ_(n=0) ^∞ (x^n /(n!)) , letting x=1 ] S_2 =Σ_(n=1) ^∞ ((3n)/(n!)) = 3e . [ e^x =Σ_(n=1) ^∞ ((nx^(n−1) )/(n!)) ] S_3 = Σ_(n=1) ^∞ ((2n(n−1))/(n!)) = 2e. [ e^x =Σ_(n=1) ^∞ ((n(n−1)x^(n−2) )/(n!))] Hence S = S_1 +S_2 +S_3 = e−1+3e+2e= 6e−1

$${S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{1}}{{n}!}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}\left({n}−\mathrm{1}\right)+\mathrm{3}{n}+\mathrm{1}}{{n}!} \\ $$$$=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}\left({n}−\mathrm{1}\right)}{{n}!}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}{n}}{{n}!}\:+\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$${S}_{\mathrm{1}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}={e}−\mathrm{1}.\:\:\left[\:{e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{{n}!}\:,\:{letting}\:{x}=\mathrm{1}\:\right]\: \\ $$$${S}_{\mathrm{2}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}{n}}{{n}!}\:=\:\mathrm{3}{e}\:.\:\left[\:{e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}−\mathrm{1}} }{{n}!}\:\right] \\ $$$${S}_{\mathrm{3}} =\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}\left({n}−\mathrm{1}\right)}{{n}!}\:=\:\mathrm{2}{e}.\:\left[\:{e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} }{{n}!}\right] \\ $$$${Hence}\:{S}\:=\:{S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} =\:{e}−\mathrm{1}+\mathrm{3}{e}+\mathrm{2}{e}=\:\mathrm{6}{e}−\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com