Question Number 114122 by bemath last updated on 17/Sep/20

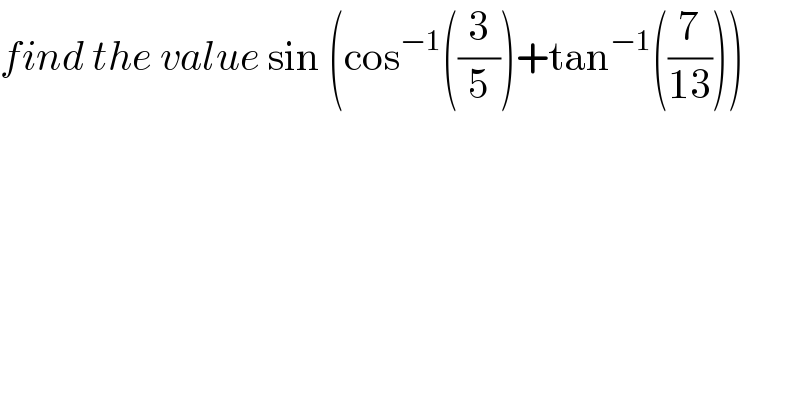
find the value sin (cos^(−1) ((3/5))+tan^(−1) ((7/(13))))

Answered by mr W last updated on 17/Sep/20

tan^(−1) (7/(13))=sin^(−1) (7/( (√(218))))=cos^(−1) ((13)/( (√(218)))) cos^(−1) (3/5)=sin^(−1) (4/5) sin (cos^(−1) ((3/5))+tan^(−1) ((7/(13)))) =(sin cos^(−1) (3/5)) (cos tan^(−1) (7/(13)))+cos (cos^(−1) (3/5)) sin (tan^(−1) (7/(13))) =(sin sin^(−1) (4/5)) (cos cos^(−1) ((13)/( (√(218)))))+cos (cos^(−1) (3/5)) sin (sin^(−1) (7/( (√(218))))) =(4/5)×((13)/( (√(218))))+(3/5)×(7/( (√(218)))) =((73)/( 5(√(218))))

Commented bybemath last updated on 17/Sep/20

santuyy