Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114192 by ZiYangLee last updated on 17/Sep/20

$$\mathrm{For}\mathrm{a}\mathrm{positive}\mathrm{integer}k,\mathrm{we}\mathrm{write}$$$$(1+x)(1+2x)(1+3x)...(1+kx)=a_0+a_{1}x+a_2{x}^2+...a_k{x}^k$$$$\mathrm{Let}N=a_0+a_1+a_2+...a_k,$$$$\mathrm{if}N\mathrm{is}\mathrm{divisible}\mathrm{by}2019,\mathrm{find}\mathrm{the}$$$$\mathrm{smallest}\mathrm{possible}\mathrm{value}\mathrm{of}k.$$

Answered by Olaf last updated on 17/Sep/20

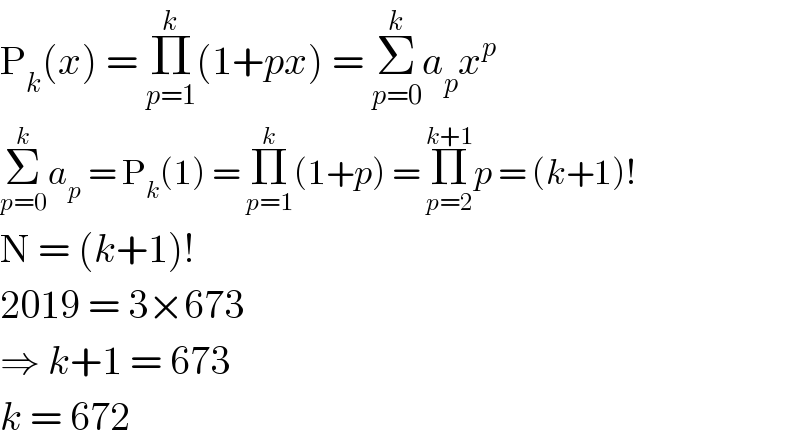
$${\mathrm{P}}_k\left(x\right)=\underset{p=1}{\prod ^k}(1+px)=\underset{p=0}{\sum ^k}{a}_p{x}^p$$$$\underset{p=0}{\sum ^k}{a}_p={\mathrm{P}}_k\left(1\right)=\underset{p=1}{\prod ^k}(1+p)=\underset{p=2}{\prod ^{k+1}}p=(k+1)!$$$$\mathrm{N}=(k+1)!$$$$2019=3\times 673$$$$\Rightarrow k+1=673$$$$k=672$$

Commented by ZiYangLee last updated on 18/Sep/20

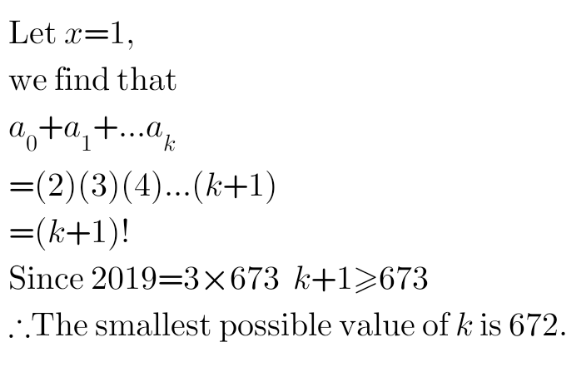
Commented by ZiYangLee last updated on 18/Sep/20

$$\mathrm{nice}\mathrm{try}!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com