
Question Number 11420 by ainstain last updated on 25/Mar/17
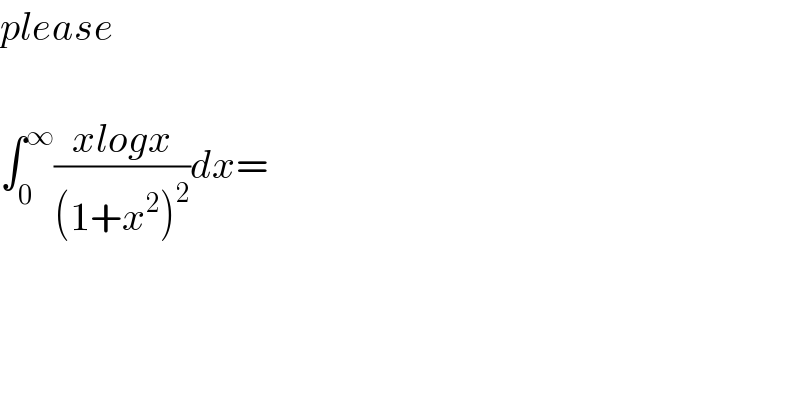
$${please} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{xlogx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}= \\ $$
Commented by FilupS last updated on 26/Mar/17

$$\mathrm{is}\:\mathrm{log}\left({x}\right)\:\mathrm{in}\:\mathrm{base}\:\mathrm{10}\:\mathrm{or}\:\mathrm{base}\:{e}? \\ $$
Answered by sm3l2996 last updated on 25/Mar/17
![{_(v′=(x/((1+x^2 )^2 ))) ^(u=log(x)) ⇒{_(v=((−1)/(2(1+x^2 )))) ^(u^′ =(1/x)) I=∫_0 ^∞ ((xlog(x))/((1+x^2 )^2 ))dx=[((−log(x))/(2(1+x^2 )))]_0 ^∞ +∫_0 ^∞ (dx/(2x(1+x^2 ))) I=lim_(x→∞) (−((log(x))/(2(1+x^2 ))))−lim_(x→0) (−((log(x))/(2(1+x^2 ))))+(1/2)∫_0 ^∞ (dx/(x(1+x^2 ))) (1/(x(1+x^2 )))=(a/x)+((bx+c)/(1+x^2 )) a=1; {_(((c−b)/2)−1=((−1)/2)) ^(((b+c)/2)+1=(1/2)) ⇔{_(c−b=1) ^(b+c=−1) b=−1; c=0 so: (1/(x(1+x^2 )))=(1/x)−(x/(1+x^2 )) ∫_0 ^∞ (dx/(x(1+x^2 )))=∫_0 ^∞ (dx/x)−∫_0 ^∞ ((xdx)/(1+x^2 )) =[log∣x∣−(1/2)log∣1+x^2 ∣]_0 ^∞ =lim_(x→+∞) log((x/(√(1+x^2 ))))−lim_(x→0) log((x/(√(1+x^2 )))) I=lim_(x→+∞) log((x/(√(1+x^2 ))))−lim_(x→0) (log((x/(√(1+x^2 ))))+((log(x))/(2(1+x^2 ))))](Q11421.png)
$$\left\{_{\mathrm{v}'=\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }} ^{\mathrm{u}=\mathrm{log}\left(\mathrm{x}\right)} \Rightarrow\left\{_{\mathrm{v}=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}} ^{\mathrm{u}^{'} =\frac{\mathrm{1}}{\mathrm{x}}} \right.\right. \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{xlog}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\left[\frac{−\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{2x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$\mathrm{I}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(−\frac{\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right)−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{bx}+\mathrm{c}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{a}=\mathrm{1};\: \\ $$$$\left\{_{\frac{\mathrm{c}−\mathrm{b}}{\mathrm{2}}−\mathrm{1}=\frac{−\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{b}+\mathrm{c}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}} \Leftrightarrow\left\{_{\mathrm{c}−\mathrm{b}=\mathrm{1}} ^{\mathrm{b}+\mathrm{c}=−\mathrm{1}} \right.\right. \\ $$$$\mathrm{b}=−\mathrm{1};\:\mathrm{c}=\mathrm{0} \\ $$$$\mathrm{so}:\:\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\left[\mathrm{log}\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\mid\mathrm{1}+\mathrm{x}^{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}log}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right)−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}log}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{I}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}log}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right)−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{log}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right)+\frac{\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right) \\ $$$$ \\ $$
Commented by sm3l2996 last updated on 25/Mar/17

$$\mathrm{working} \\ $$
Answered by ajfour last updated on 26/Mar/17

$$\mathrm{zero} \\ $$
