
Question Number 114208 by aurpeyz last updated on 17/Sep/20

$${find}\:{the}\:{greatest}\:{coeeficient}\:{in}\:{the}\:{expansion} \\ $$$${of}\:\left(\mathrm{3}+\mathrm{4}{x}\right)^{−\mathrm{5}} \\ $$
Commented by I want to learn more last updated on 17/Sep/20

$$\mathrm{Please}\:\mathrm{how}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 17/Sep/20
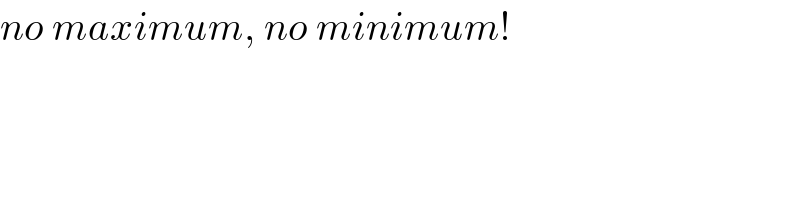
$${no}\:{maximum},\:{no}\:{minimum}! \\ $$
Commented by aurpeyz last updated on 18/Sep/20

$${why}? \\ $$
Commented by mr W last updated on 18/Sep/20
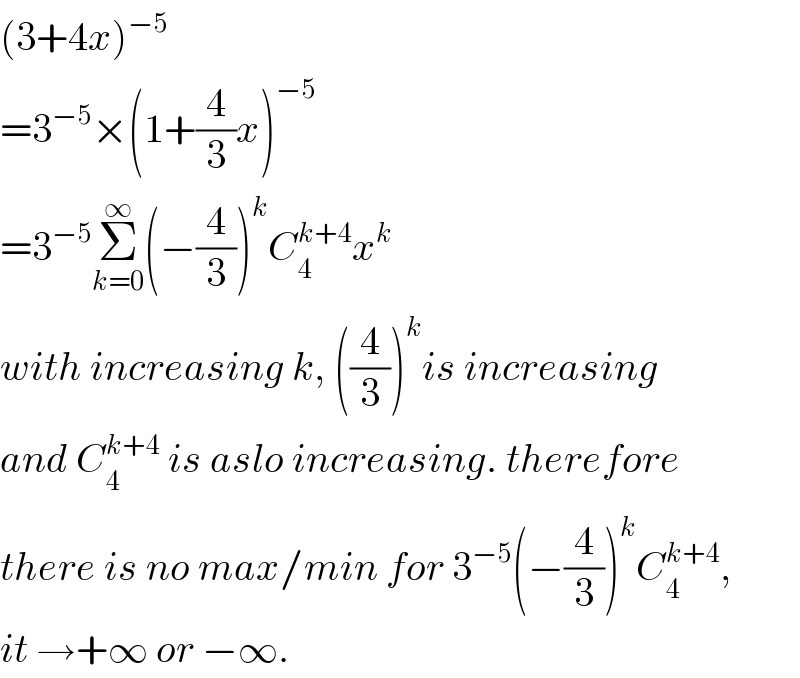
$$\left(\mathrm{3}+\mathrm{4}{x}\right)^{−\mathrm{5}} \\ $$$$=\mathrm{3}^{−\mathrm{5}} ×\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{3}}{x}\right)^{−\mathrm{5}} \\ $$$$=\mathrm{3}^{−\mathrm{5}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{4}}{\mathrm{3}}\right)^{{k}} {C}_{\mathrm{4}} ^{{k}+\mathrm{4}} {x}^{{k}} \\ $$$${with}\:{increasing}\:{k},\:\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{k}} {is}\:{increasing} \\ $$$${and}\:{C}_{\mathrm{4}} ^{{k}+\mathrm{4}} \:{is}\:{aslo}\:{increasing}.\:{therefore} \\ $$$${there}\:{is}\:{no}\:{max}/{min}\:{for}\:\mathrm{3}^{−\mathrm{5}} \left(−\frac{\mathrm{4}}{\mathrm{3}}\right)^{{k}} {C}_{\mathrm{4}} ^{{k}+\mathrm{4}} , \\ $$$${it}\:\rightarrow+\infty\:{or}\:−\infty. \\ $$
Commented by aurpeyz last updated on 18/Sep/20
$${i}\:{think}\:{there}\:{is}\:{more}\:{to}\:{this}\:{topic}\:{than}\:{i}\:{know} \\ $$
Commented by mr W last updated on 18/Sep/20

$${with}\:{that}\:{what}\:{you}\:{know}\:{you}\:{can} \\ $$$${solve}\:{alot}\:{of}\:{questions},\:{such}\:{as}\:{this} \\ $$$${one}.\:{just}\:{apply}! \\ $$
Commented by aurpeyz last updated on 18/Sep/20

$${thanks}\:{alot}\:{Sir} \\ $$
Commented by aurpeyz last updated on 18/Sep/20
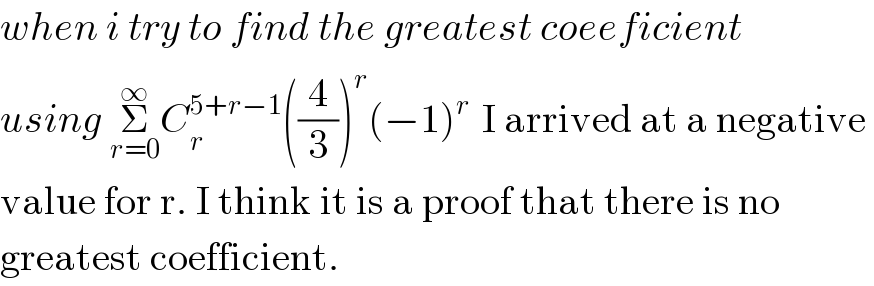
$${when}\:{i}\:{try}\:{to}\:{find}\:{the}\:{greatest}\:{coeeficient} \\ $$$${using}\:\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{r}} ^{\mathrm{5}+{r}−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{r}} \left(−\mathrm{1}\right)^{{r}\:} \:\mathrm{I}\:\mathrm{arrived}\:\mathrm{at}\:\mathrm{a}\:\mathrm{negative}\: \\ $$$$\mathrm{value}\:\mathrm{for}\:\mathrm{r}.\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\: \\ $$$$\mathrm{greatest}\:\mathrm{coefficient}. \\ $$
Commented by mr W last updated on 18/Sep/20

$${no}\:{proof}\:{needed}.\:{it}'{s}\:{clear}: \\ $$$${C}_{\mathrm{4}} ^{\mathrm{4}+{r}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{r}} \:{is}\:{always}\:{increasing}\:{and} \\ $$$$\left(−\mathrm{1}\right)^{{r}\:} =\mathrm{1}\:{for}\:{even}\:{r}\:{and}\:−\mathrm{1}\:{for}\:{odd}\:{r}. \\ $$$${so}\:{there}\:{is}\:{neither}\:{maximum}\:{nor} \\ $$$${minimum}\:{coefficient}. \\ $$
Commented by mr W last updated on 18/Sep/20
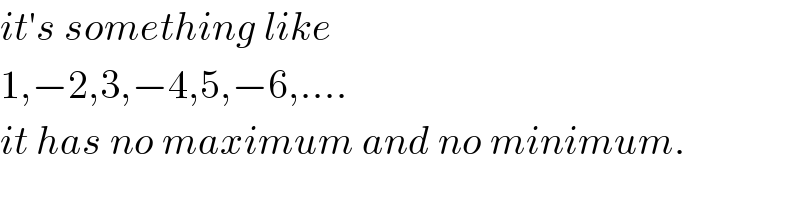
$${it}'{s}\:{something}\:{like} \\ $$$$\mathrm{1},−\mathrm{2},\mathrm{3},−\mathrm{4},\mathrm{5},−\mathrm{6},.... \\ $$$${it}\:{has}\:{no}\:{maximum}\:{and}\:{no}\:{minimum}. \\ $$
Commented by aurpeyz last updated on 18/Sep/20

$${anytime}\:{i}\:{have}\:{a}\:{question}.\:{how}\:{can}\:{i}\:{know} \\ $$$${without}\:{proof}\:{that}\:{there}\:{is}\:{no}\:{max}\:{or}\:{min}. \\ $$$${did}\:{you}\:{determine}\:{it}\:{by}\:\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{r}} \:{or}\:{the}\:{nature} \\ $$$${of}\:{the}\:{question}\:{being}\:\left(\mathrm{3}+\mathrm{4}{x}\right)^{−\mathrm{5}} . \\ $$$$ \\ $$$${i}\:{have}\:{not}\:{seen}\:{any}\:{textbook}\:{that}\:{deals}\:{with} \\ $$$${greatest}\:{coefficient}\:{of}\:{question}\:{like}\:{that}.\: \\ $$$${i}\:{thought}\:{it}\:{is}\:{because}\:{of}\:{the}\:{positive}\:{sign}\:\left(+\right)\: \\ $$$${between}\:{the}\:{binomial}. \\ $$$$ \\ $$$${what}\:{if}\:{we}\:{had}\:{a}\:{question}\:{with}\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{x}} \:? \\ $$
Commented by mr W last updated on 18/Sep/20
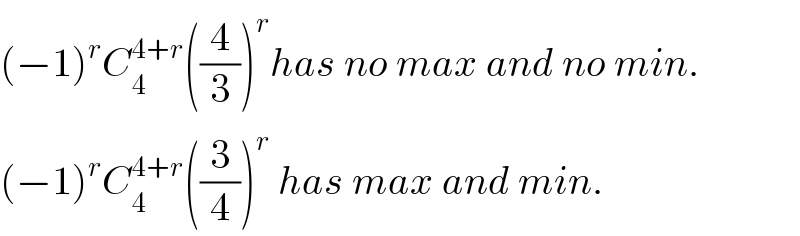
$$\left(−\mathrm{1}\right)^{{r}} {C}_{\mathrm{4}} ^{\mathrm{4}+{r}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{{r}} {has}\:{no}\:{max}\:{and}\:{no}\:{min}. \\ $$$$\left(−\mathrm{1}\right)^{{r}} {C}_{\mathrm{4}} ^{\mathrm{4}+{r}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{r}} \:{has}\:{max}\:{and}\:{min}. \\ $$
Commented by aurpeyz last updated on 18/Sep/20
$${thank}\:{you}\:{Sir}.\:{i}\:{will}\:{attempt}\:{it} \\ $$
Commented by aurpeyz last updated on 18/Sep/20
![lets say i have (4+3x)^(−5) (4+3x)^(−5) =4^(−5) [(−1)^r Σ_(r=0) ^∞ C_r ^(4+r) ((3/4))^r ] (−1)^r C_r ^(4+r) ((3/4))^r ≥ (−1)^(r+1) C_(r+1) ^(5+r) ((3/4)) C_4 ^(4+r) ≥(−1)C_4 ^(5+r) ((3/4))^1 r=((−19)/7). the negativity gives me issue. is it that any question like (4+3x)^(−5) [with positive sign in between binomial of negative powers] usually dont have max or min?](Q114381.png)
$${lets}\:{say}\:{i}\:{have}\:\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} \\ $$$$\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} =\mathrm{4}^{−\mathrm{5}} \left[\left(−\mathrm{1}\right)^{{r}} \underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{r}} ^{\mathrm{4}+{r}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{r}} \right] \\ $$$$\left(−\mathrm{1}\right)^{{r}} {C}_{{r}} ^{\mathrm{4}+{r}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{r}} \geqslant\:\left(−\mathrm{1}\right)^{{r}+\mathrm{1}} {C}_{{r}+\mathrm{1}} ^{\mathrm{5}+{r}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${C}_{\mathrm{4}} ^{\mathrm{4}+{r}} \geqslant\left(−\mathrm{1}\right){C}_{\mathrm{4}} ^{\mathrm{5}+{r}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{1}} \\ $$$${r}=\frac{−\mathrm{19}}{\mathrm{7}}.\: \\ $$$${the}\:{negativity}\:{gives}\:{me}\:{issue}. \\ $$$$ \\ $$$${is}\:{it}\:{that}\:{any}\:{question}\:{like}\:\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} \:\left[{with}\:\right. \\ $$$${positive}\:{sign}\:{in}\:{between}\:{binomial}\:{of}\:{negative} \\ $$$$\left.{powers}\right]\:{usually}\:{dont}\:{have}\:{max}\:{or}\:{min}? \\ $$
Commented by mr W last updated on 18/Sep/20
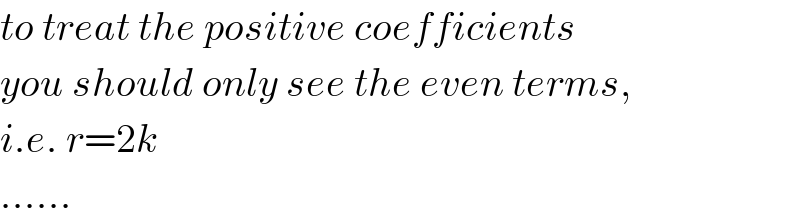
$${to}\:{treat}\:{the}\:{positive}\:{coefficients} \\ $$$${you}\:{should}\:{only}\:{see}\:{the}\:{even}\:{terms}, \\ $$$${i}.{e}.\:{r}=\mathrm{2}{k} \\ $$$$...... \\ $$
Commented by aurpeyz last updated on 19/Sep/20

$${please}\:{shed}\:{little}\:{light}\:{on}\:{this}.\:{r}=\mathrm{2}{k}?\:{how} \\ $$$${is}\:{this}\:{done}? \\ $$
Commented by mr W last updated on 19/Sep/20

$${even}\:{terms}\:\left({r}=\mathrm{2}{k}\right)\:{have}\:{positive}\: \\ $$$${coefficients},\:{odd}\:{terms}\:\left({r}=\mathrm{2}{k}+\mathrm{1}\right) \\ $$$${have}\:{negative}\:{coefficients}.\:{just}\:{think}! \\ $$
Commented by aurpeyz last updated on 20/Sep/20

$${okay}\: \\ $$
