Question and Answers Forum

All Questions      Topic List

Set Theory Questions

Previous in All Question      Next in All Question      

Previous in Set Theory      Next in Set Theory      

Question Number 114235 by Aina Samuel Temidayo last updated on 18/Sep/20

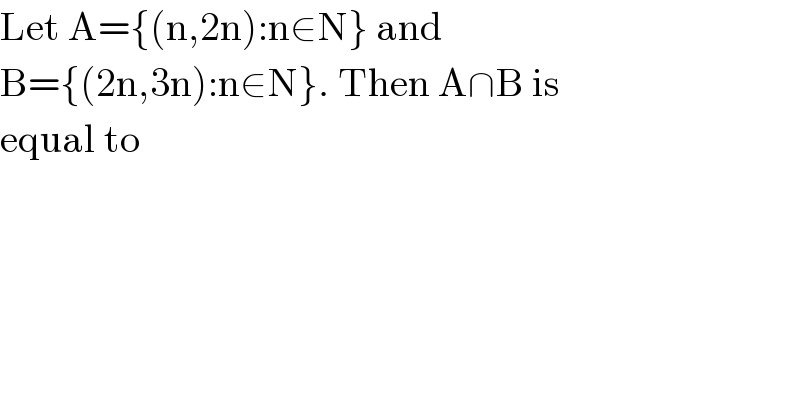
Let A={(n,2n):n∈N} and B={(2n,3n):n∈N}. Then A∩B is equal to

$$\mathrm{Let}\:\mathrm{A}=\left\{\left(\mathrm{n},\mathrm{2n}\right):\mathrm{n}\in\mathrm{N}\right\}\:\mathrm{and} \\ $$$$\mathrm{B}=\left\{\left(\mathrm{2n},\mathrm{3n}\right):\mathrm{n}\in\mathrm{N}\right\}.\:\mathrm{Then}\:\mathrm{A}\cap\mathrm{B}\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$

Answered by 1549442205PVT last updated on 18/Sep/20

A∩B=(0,0)since (0,0)=(0;2.0)=(2.0;3.0)

$$\mathrm{A}\cap\mathrm{B}=\left(\mathrm{0},\mathrm{0}\right)\mathrm{since} \\ $$$$\left(\mathrm{0},\mathrm{0}\right)=\left(\mathrm{0};\mathrm{2}.\mathrm{0}\right)=\left(\mathrm{2}.\mathrm{0};\mathrm{3}.\mathrm{0}\right) \\ $$

Commented by Aina Samuel Temidayo last updated on 18/Sep/20

Not correct.

$$\mathrm{Not}\:\mathrm{correct}. \\ $$

Commented by MJS_new last updated on 18/Sep/20

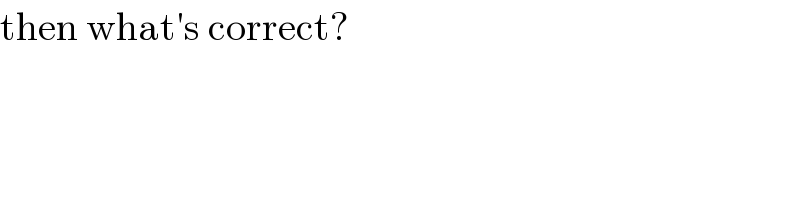
then what′s correct?

$$\mathrm{then}\:\mathrm{what}'\mathrm{s}\:\mathrm{correct}? \\ $$

Commented by 1549442205PVT last updated on 18/Sep/20

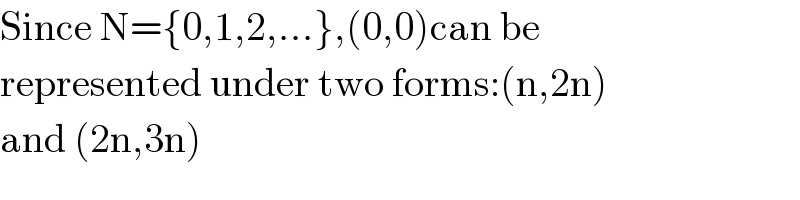
Since N={0,1,2,...},(0,0)can be represented under two forms:(n,2n) and (2n,3n)

$$\mathrm{Since}\:\mathrm{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},...\right\},\left(\mathrm{0},\mathrm{0}\right)\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{represented}\:\mathrm{under}\:\mathrm{two}\:\mathrm{forms}:\left(\mathrm{n},\mathrm{2n}\right) \\ $$$$\mathrm{and}\:\left(\mathrm{2n},\mathrm{3n}\right) \\ $$

Answered by malwaan last updated on 18/Sep/20

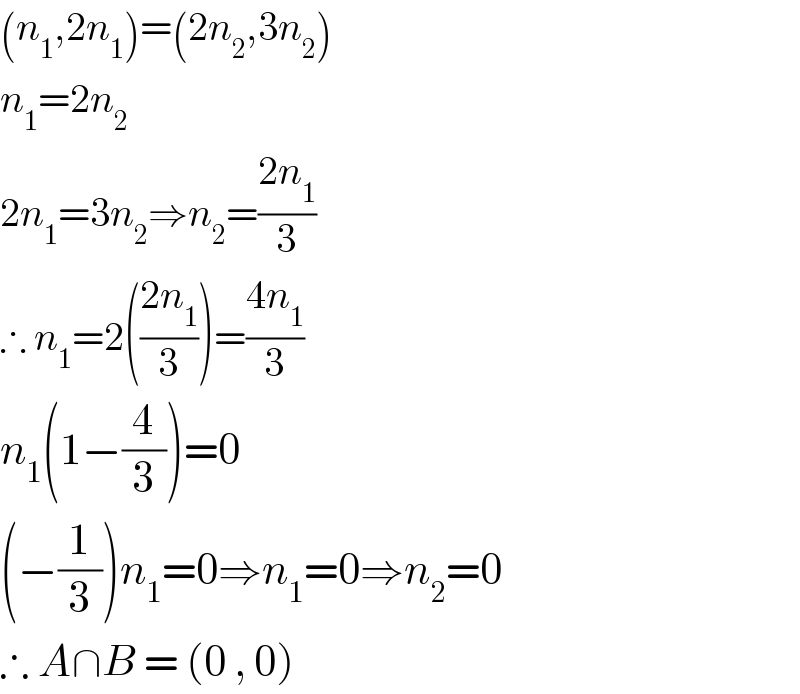
(n_1 ,2n_1 )=(2n_2 ,3n_2 ) n_1 =2n_2 2n_1 =3n_2 ⇒n_2 =((2n_1 )/3) ∴ n_1 =2(((2n_1 )/3))=((4n_1 )/3) n_1 (1−(4/3))=0 (−(1/3))n_1 =0⇒n_1 =0⇒n_2 =0 ∴ A∩B = (0 , 0)

$$\left({n}_{\mathrm{1}} ,\mathrm{2}{n}_{\mathrm{1}} \right)=\left(\mathrm{2}{n}_{\mathrm{2}} ,\mathrm{3}{n}_{\mathrm{2}} \right) \\ $$$${n}_{\mathrm{1}} =\mathrm{2}{n}_{\mathrm{2}} \\ $$$$\mathrm{2}{n}_{\mathrm{1}} =\mathrm{3}{n}_{\mathrm{2}} \Rightarrow{n}_{\mathrm{2}} =\frac{\mathrm{2}{n}_{\mathrm{1}} }{\mathrm{3}} \\ $$$$\therefore\:{n}_{\mathrm{1}} =\mathrm{2}\left(\frac{\mathrm{2}{n}_{\mathrm{1}} }{\mathrm{3}}\right)=\frac{\mathrm{4}{n}_{\mathrm{1}} }{\mathrm{3}} \\ $$$${n}_{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{3}}\right){n}_{\mathrm{1}} =\mathrm{0}\Rightarrow{n}_{\mathrm{1}} =\mathrm{0}\Rightarrow{n}_{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore\:{A}\cap{B}\:=\:\left(\mathrm{0}\:,\:\mathrm{0}\right) \\ $$

Commented by Aina Samuel Temidayo last updated on 19/Sep/20

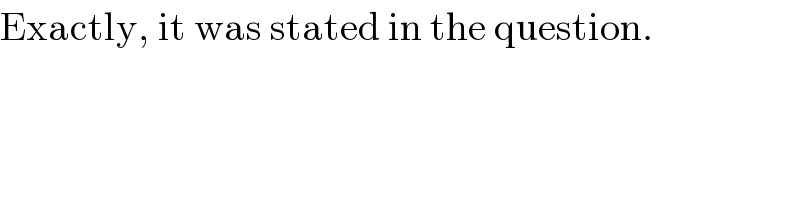
Exactly, it was stated in the question.

$$\mathrm{Exactly},\:\mathrm{it}\:\mathrm{was}\:\mathrm{stated}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$

Commented by 1549442205PVT last updated on 18/Sep/20

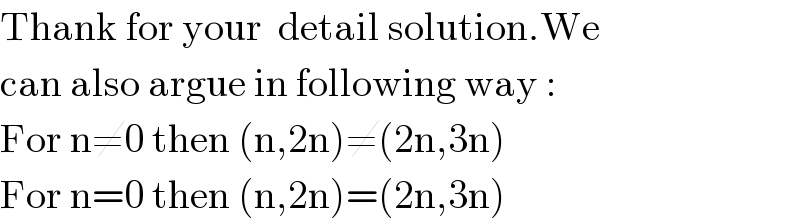
Thank for your detail solution.We can also argue in following way : For n≠0 then (n,2n)≠(2n,3n) For n=0 then (n,2n)=(2n,3n)

$$\mathrm{Thank}\:\mathrm{for}\:\mathrm{your}\:\:\mathrm{detail}\:\mathrm{solution}.\mathrm{We} \\ $$$$\mathrm{can}\:\mathrm{also}\:\mathrm{argue}\:\mathrm{in}\:\mathrm{following}\:\mathrm{way}\:: \\ $$$$\mathrm{For}\:\mathrm{n}\neq\mathrm{0}\:\mathrm{then}\:\left(\mathrm{n},\mathrm{2n}\right)\neq\left(\mathrm{2n},\mathrm{3n}\right) \\ $$$$\mathrm{For}\:\mathrm{n}=\mathrm{0}\:\mathrm{then}\:\left(\mathrm{n},\mathrm{2n}\right)=\left(\mathrm{2n},\mathrm{3n}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 18/Sep/20

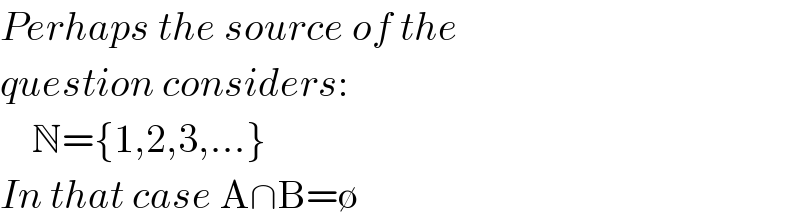
Perhaps the source of the question considers: N={1,2,3,...} In that case A∩B=∅

$${Perhaps}\:{the}\:{source}\:{of}\:{the} \\ $$$${question}\:{considers}: \\ $$$$\:\:\:\:\mathbb{N}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$$${In}\:{that}\:{case}\:\mathrm{A}\cap\mathrm{B}=\emptyset \\ $$

Commented by MJS_new last updated on 19/Sep/20

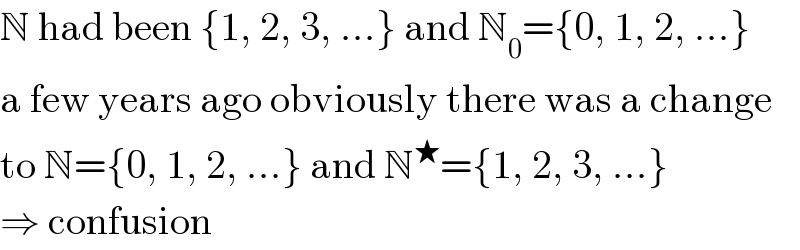
N had been {1, 2, 3, ...} and N_0 ={0, 1, 2, ...} a few years ago obviously there was a change to N={0, 1, 2, ...} and N^★ ={1, 2, 3, ...} ⇒ confusion

$$\mathbb{N}\:\mathrm{had}\:\mathrm{been}\:\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\}\:\mathrm{and}\:\mathbb{N}_{\mathrm{0}} =\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:...\right\} \\ $$$$\mathrm{a}\:\mathrm{few}\:\mathrm{years}\:\mathrm{ago}\:\mathrm{obviously}\:\mathrm{there}\:\mathrm{was}\:\mathrm{a}\:\mathrm{change} \\ $$$$\mathrm{to}\:\mathbb{N}=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:...\right\}\:\mathrm{and}\:\mathbb{N}^{\bigstar} =\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\} \\ $$$$\Rightarrow\:\mathrm{confusion} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com