
Question Number 11429 by @ANTARES_VY last updated on 25/Mar/17
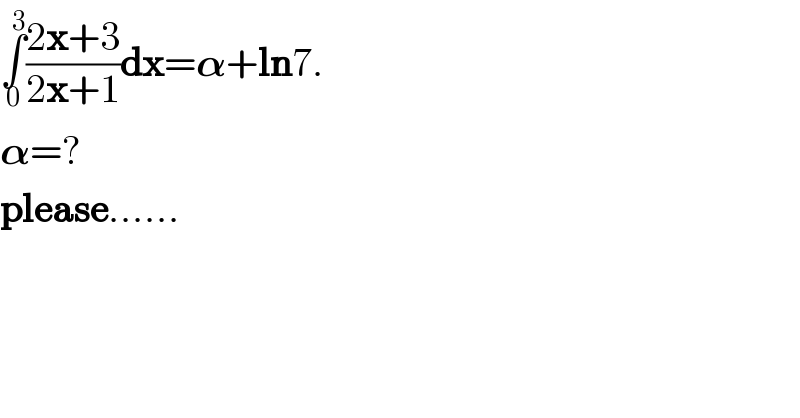
$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{3}}{\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}}\boldsymbol{\mathrm{dx}}=\boldsymbol{\alpha}+\boldsymbol{\mathrm{ln}}\mathrm{7}. \\ $$$$\boldsymbol{\alpha}=? \\ $$$$\boldsymbol{\mathrm{please}}...... \\ $$
Answered by FilupS last updated on 26/Mar/17
![((2x+3)/(2x+1))=((2x+1+2)/(2x+1))=1+(2/(2x+1)) ∫_0 ^( 3) ((2x+3)/(2x+1))dx=∫_0 ^( 3) 1+(2/(2x+1))dx =∫_0 ^( 3) 1dx+∫_0 ^( 3) (2/(2x+1))dx =[x]_0 ^3 +[ln(2x+1)]_0 ^3 =(3−0)+(ln(7)−ln(1)) =3+ln(7) ∴α=3 red text is corrected](Q11430.png)
$$\frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}+\mathrm{1}}=\frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{3}} \frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}+\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\:\mathrm{3}} \mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{3}} \mathrm{1}{dx}+\int_{\mathrm{0}} ^{\:\mathrm{3}} \frac{\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$$$=\left[{x}\right]_{\mathrm{0}} ^{\mathrm{3}} +\left[\mathrm{ln}\left(\mathrm{2}{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$=\left(\mathrm{3}−\mathrm{0}\right)+\left(\mathrm{ln}\left(\mathrm{7}\right)−\mathrm{ln}\left(\mathrm{1}\right)\right) \\ $$$$=\mathrm{3}+\mathrm{ln}\left(\mathrm{7}\right) \\ $$$$\: \\ $$$$\therefore\alpha=\mathrm{3} \\ $$$$\: \\ $$$$\mathrm{red}\:\mathrm{text}\:\mathrm{is}\:\mathrm{corrected} \\ $$
Commented by @ANTARES_VY last updated on 26/Mar/17

$$\boldsymbol{\alpha}=\mathrm{2}?... \\ $$
Commented by FilupS last updated on 26/Mar/17

$$\mathrm{yes} \\ $$
Commented by @ANTARES_VY last updated on 26/Mar/17

$$\boldsymbol{\mathrm{such}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{wrong}}\:\:\boldsymbol{\mathrm{answer}}.... \\ $$$$\boldsymbol{\mathrm{no}}\:\:\boldsymbol{\alpha}=\mathrm{2}????? \\ $$
Commented by FilupS last updated on 26/Mar/17
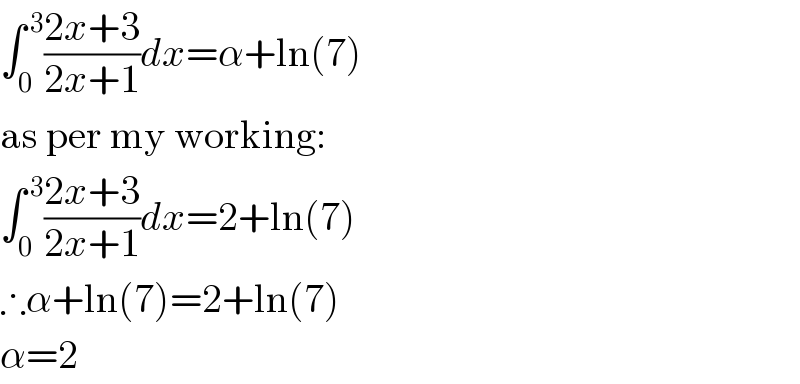
$$\int_{\mathrm{0}} ^{\:\mathrm{3}} \frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}+\mathrm{1}}{dx}=\alpha+\mathrm{ln}\left(\mathrm{7}\right) \\ $$$$\mathrm{as}\:\mathrm{per}\:\mathrm{my}\:\mathrm{working}: \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{3}} \frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}+\mathrm{1}}{dx}=\mathrm{2}+\mathrm{ln}\left(\mathrm{7}\right) \\ $$$$\therefore\alpha+\mathrm{ln}\left(\mathrm{7}\right)=\mathrm{2}+\mathrm{ln}\left(\mathrm{7}\right) \\ $$$$\alpha=\mathrm{2} \\ $$
Commented by ajfour last updated on 26/Mar/17
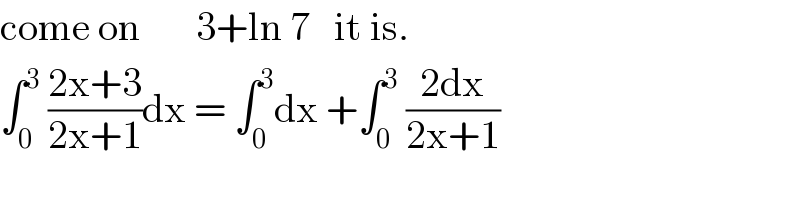
$$\mathrm{come}\:\mathrm{on}\:\:\:\:\:\:\:\mathrm{3}+\mathrm{ln}\:\mathrm{7}\:\:\:\mathrm{it}\:\mathrm{is}. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}+\mathrm{1}}\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{dx}\:+\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{2dx}}{\mathrm{2x}+\mathrm{1}} \\ $$
Commented by FilupS last updated on 26/Mar/17

$$\mathrm{I}\:\mathrm{see}\:\mathrm{my}\:\mathrm{mistake}. \\ $$$$\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{bad}\:\mathrm{typo}.\:\mathrm{Sorry} \\ $$
