Question Number 114395 by mathmax by abdo last updated on 18/Sep/20

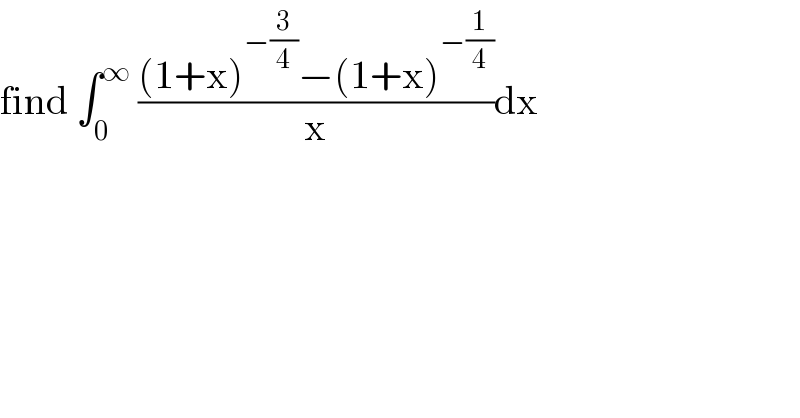
find ∫_0 ^∞ (((1+x)^(−(3/4)) −(1+x)^(−(1/4)) )/x)dx

Answered by Olaf last updated on 19/Sep/20

I = ∫_0 ^∞ (((1+x)^(−(3/4)) −(1+x)^(−(1/4)) )/x)dx u = (1+x)^(1/4) du = (1/4)(1+x)^(−(3/4)) dx = (dx/(4u^3 )) I = ∫_1 ^∞ (((1/u^3 )−(1/u))/(u^4 −1)).4u^3 du I = 4∫_1 ^∞ ((1−u^2 )/(u^4 −1))du I = −4∫_1 ^∞ (du/(1+u^2 )) I = −4[arctanu]_1 ^∞ = −4((π/2)−(π/4)) = −π