
Question Number 114422 by Aina Samuel Temidayo last updated on 19/Sep/20
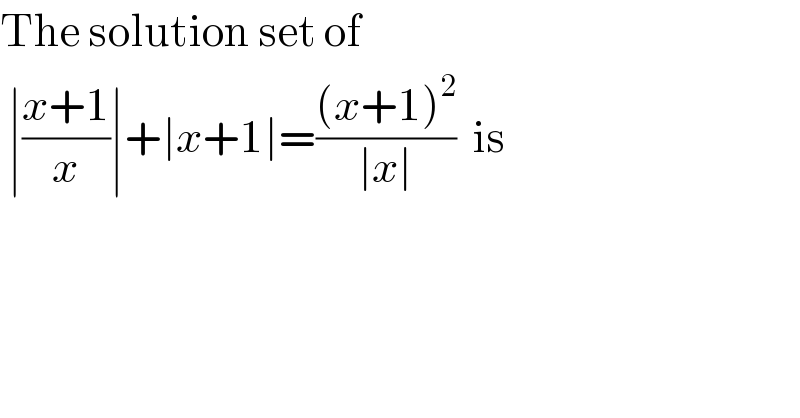
$$\mathrm{The}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\: \\ $$$$\:\mid\frac{{x}+\mathrm{1}}{{x}}\mid+\mid{x}+\mathrm{1}\mid=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid{x}\mid}\:\:\mathrm{is} \\ $$
Commented by bemath last updated on 19/Sep/20
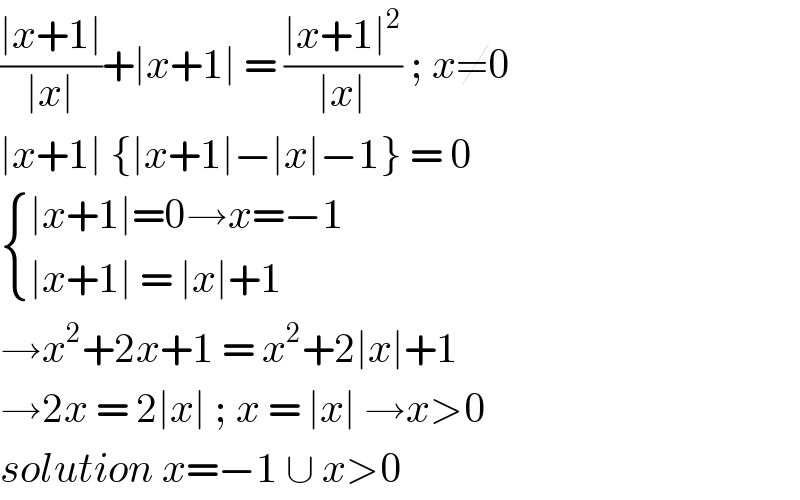
$$\frac{\mid{x}+\mathrm{1}\mid}{\mid{x}\mid}+\mid{x}+\mathrm{1}\mid\:=\:\frac{\mid{x}+\mathrm{1}\mid^{\mathrm{2}} }{\mid{x}\mid}\:;\:{x}\neq\mathrm{0} \\ $$$$\mid{x}+\mathrm{1}\mid\:\left\{\mid{x}+\mathrm{1}\mid−\mid{x}\mid−\mathrm{1}\right\}\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mid{x}+\mathrm{1}\mid=\mathrm{0}\rightarrow{x}=−\mathrm{1}}\\{\mid{x}+\mathrm{1}\mid\:=\:\mid{x}\mid+\mathrm{1}}\end{cases} \\ $$$$\rightarrow{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\:=\:{x}^{\mathrm{2}} +\mathrm{2}\mid{x}\mid+\mathrm{1} \\ $$$$\rightarrow\mathrm{2}{x}\:=\:\mathrm{2}\mid{x}\mid\:;\:{x}\:=\:\mid{x}\mid\:\rightarrow{x}>\mathrm{0} \\ $$$${solution}\:{x}=−\mathrm{1}\:\cup\:{x}>\mathrm{0} \\ $$
Commented by Aina Samuel Temidayo last updated on 19/Sep/20

$$\mathrm{This}\:\mathrm{is}\:\mathrm{not}\:\mathrm{its}\:\mathrm{only}\:\mathrm{solution}. \\ $$
Commented by bemath last updated on 19/Sep/20

$${it}\:{only}\:{solution} \\ $$
Answered by 1549442205PVT last updated on 19/Sep/20

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{eqution} \\ $$$$\:\mid\frac{{x}+\mathrm{1}}{{x}}\mid+\mid{x}+\mathrm{1}\mid=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid{x}\mid}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{x}\neq\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{the}\:\mathrm{following}\:\mathrm{tablet}: \\ $$$$\begin{vmatrix}{\mathrm{x}}&{}&{−\mathrm{1}}&{}&{\mathrm{0}}&{}\\{\mid\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}\mid}&{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}&{\mathrm{0}}&{−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}&{\mid\mid}&{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}\\{\mid\mathrm{x}+\mathrm{1}\mid}&{−\mathrm{x}−\mathrm{1}}&{\mathrm{0}}&{\mathrm{x}+\mathrm{1}}&{\mathrm{1}}&{\mathrm{x}+\mathrm{1}}\\{\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid\mathrm{x}\mid}}&{−\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}}}&{\mathrm{0}}&{−\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}}}&{\mid\mid}&{\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}}}\end{vmatrix} \\ $$$$\mathrm{From}\:\mathrm{above}\:\mathrm{tablet}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\:\mathrm{x}\leqslant−\mathrm{1}\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}−\mathrm{x}−\mathrm{1}=−\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2x}+\mathrm{2}=\mathrm{0}\Leftrightarrow\mathrm{x}+\mathrm{1}=\mathrm{0}\Leftrightarrow\mathrm{x}=−\mathrm{1} \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:−\mathrm{1}<\mathrm{x}<\mathrm{0}\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}+\mathrm{x}+\mathrm{1}=−\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)−\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{0}\Leftrightarrow\mathrm{2x}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left.\Leftrightarrow\mathrm{x}+\mathrm{1}=\mathrm{0}\:\left(\mathrm{rejected}\:\mathrm{as}\:\mathrm{don}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{ii}\right)\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{If}\:\mathrm{x}>\mathrm{0}\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}+\mathrm{x}+\mathrm{1}=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)−\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{0}.\mathrm{x}=\mathrm{0}\Rightarrow\forall\mathrm{x}>\mathrm{0}\:\mathrm{are}\:\mathrm{roots} \\ $$$$\mathrm{Combining}\:\mathrm{three}\:\mathrm{above}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{are} \\ $$$$\mathrm{x}\in\left\{−\mathrm{1}\right\}\cup\left(\mathrm{0};+\infty\right) \\ $$
Answered by Aina Samuel Temidayo last updated on 19/Sep/20
![= ((∣x+1∣)/(∣x∣))+∣x+1∣ = (((x+1)^2 )/(∣x∣)), x≠0 CASE I: when x+1≥0 and x≥0 x≥−1 and x≥0 Finding their intersections ⇒ x≥0 but x≠0 ⇒ x>0 ⇒ ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) = ((x+1)/x)+x+1= ((x^2 +2x+1)/x) ⇒ x+1+x^2 +x= x^2 +2x+1 ⇒ 0=0 ⇒ x∈R Recall x>0 ⇒ x>0 CASE II: when x+1<0 and x<0 ⇒ x<−1 and x<0 ⇒ x<−1 ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) =((−(x+1))/(−(x)))+(−(x+1))= ((x^2 +2x+1)/(−(x))) ⇒−x−1+(−x(−(x+1)))=x^2 +2x+1 ⇒−x−1+(−x(−x−1))=x^2 +2x+1 ⇒−x−1+x^2 +x=x^2 +2x+1 ⇒x=−1 since x<−1 ⇒ x∈φ CASE III: when x+1<0 and x≥0 ⇒ x<−1 and x≥0 Finding their intersections ⇒ x∈φ CASE IV: when x+1≥0 and x<0 ⇒ x≥−1 and x<0 ⇒ x∈ [−1,0) ⇒∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) ⇒((x+1)/(−x))+x+1=((x^2 +2x+1)/(−x)) ⇒(x+1)−x(x+1)=x^2 +2x+1 ⇒ x+1−x^2 −x=x^2 +2x+1 ⇒ 2x^2 +2x=0 ⇒x(x+1)=0 ⇒x=0 or x=−1 since x∈[−1,0) ⇒ x=−1 Combining Cases I,II,III and IV ⇒ x∈ (0,+∞) ∪ [−1] ⇒ x∈ {−1} ∪ (0,+∞)](Q114426.png)
$$=\:\frac{\mid\mathrm{x}+\mathrm{1}\mid}{\mid\mathrm{x}\mid}+\mid\mathrm{x}+\mathrm{1}\mid\:=\:\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid\mathrm{x}\mid},\:\mathrm{x}\neq\mathrm{0} \\ $$$$\mathrm{CASE}\:\mathrm{I}: \\ $$$$\mathrm{when}\:\mathrm{x}+\mathrm{1}\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{x}\geqslant−\mathrm{1}\:\mathrm{and}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{Finding}\:\mathrm{their}\:\mathrm{intersections} \\ $$$$\Rightarrow\:\mathrm{x}\geqslant\mathrm{0}\: \\ $$$$\mathrm{but}\:\mathrm{x}\neq\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\mid\frac{{x}+\mathrm{1}}{{x}}\mid+\mid{x}+\mathrm{1}\mid=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid{x}\mid}\: \\ $$$$=\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}+\mathrm{x}+\mathrm{1}=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}{\mathrm{x}} \\ $$$$\Rightarrow\:\mathrm{x}+\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{0}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{Recall}\:\mathrm{x}>\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{CASE}\:\mathrm{II}: \\ $$$$\mathrm{when}\:\mathrm{x}+\mathrm{1}<\mathrm{0}\:\mathrm{and}\:\mathrm{x}<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}<−\mathrm{1}\:\mathrm{and}\:\mathrm{x}<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}<−\mathrm{1} \\ $$$$\:\mid\frac{{x}+\mathrm{1}}{{x}}\mid+\mid{x}+\mathrm{1}\mid=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid{x}\mid}\: \\ $$$$=\frac{−\left(\mathrm{x}+\mathrm{1}\right)}{−\left(\mathrm{x}\right)}+\left(−\left(\mathrm{x}+\mathrm{1}\right)\right)=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}{−\left(\mathrm{x}\right)} \\ $$$$\Rightarrow−\mathrm{x}−\mathrm{1}+\left(−\mathrm{x}\left(−\left(\mathrm{x}+\mathrm{1}\right)\right)\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow−\mathrm{x}−\mathrm{1}+\left(−\mathrm{x}\left(−\mathrm{x}−\mathrm{1}\right)\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow−\mathrm{x}−\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{since}\:\mathrm{x}<−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}\in\phi \\ $$$$ \\ $$$$\mathrm{CASE}\:\mathrm{III}: \\ $$$$\mathrm{when}\:\mathrm{x}+\mathrm{1}<\mathrm{0}\:\mathrm{and}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}<−\mathrm{1}\:\mathrm{and}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{Finding}\:\mathrm{their}\:\mathrm{intersections} \\ $$$$\Rightarrow\:\mathrm{x}\in\phi \\ $$$$ \\ $$$$\mathrm{CASE}\:\mathrm{IV}: \\ $$$$\mathrm{when}\:\mathrm{x}+\mathrm{1}\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{x}<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\geqslant−\mathrm{1}\:\mathrm{and}\:\mathrm{x}<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\in\:\left[−\mathrm{1},\mathrm{0}\right) \\ $$$$\:\Rightarrow\mid\frac{{x}+\mathrm{1}}{{x}}\mid+\mid{x}+\mathrm{1}\mid=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mid{x}\mid}\:\: \\ $$$$\Rightarrow\frac{\mathrm{x}+\mathrm{1}}{−\mathrm{x}}+\mathrm{x}+\mathrm{1}=\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}{−\mathrm{x}} \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{x}+\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{x}=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{0}\:\mathrm{or}\:\mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{since}\:\mathrm{x}\in\left[−\mathrm{1},\mathrm{0}\right) \\ $$$$\Rightarrow\:\mathrm{x}=−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{Combining}\:\mathrm{Cases}\:\mathrm{I},\mathrm{II},\mathrm{III}\:\mathrm{and}\:\mathrm{IV} \\ $$$$\Rightarrow\:\mathrm{x}\in\:\left(\mathrm{0},+\infty\right)\:\cup\:\left[−\mathrm{1}\right] \\ $$$$\Rightarrow\:\mathrm{x}\in\:\left\{−\mathrm{1}\right\}\:\cup\:\left(\mathrm{0},+\infty\right) \\ $$$$ \\ $$
Commented by ruwedkabeh last updated on 19/Sep/20

$${Case}\:{II} \\ $$$$−\left({x}+\mathrm{1}\right) \\ $$
Commented by Aina Samuel Temidayo last updated on 19/Sep/20
$$\mathrm{What}\:\mathrm{was}\:\mathrm{my}\:\mathrm{error}\:\mathrm{please}? \\ $$
Commented by Aina Samuel Temidayo last updated on 19/Sep/20

$$\mathrm{Corrected}.\:\mathrm{Thanks}\overset{} {.} \\ $$
Answered by mnjuly1970 last updated on 19/Sep/20
![solution::(x+1)^2 =∣x+1∣^2 ∣x+1∣((1/(∣x∣))+1−((∣x+1∣)/(∣x∣)))=0 x=−1 ✓ or (1/(∣x∣))+1−((∣x+1∣)/(∣x∣))=0 if x<−1 ⇒−(1/x)+1+[((x+1)/x)=1+(1/x)]=0 2=0 impossible if −1≤x≤0 ⇒ −(1/x)+1−1−(1/x)=0⇒((−2)/x)=0 again it is impossible. x>0⇒ (1/x)+1−1−(1/x)=0 ✓✓ ans {−1}∪ x>0 ✓](Q114523.png)
$${solution}::\left({x}+\mathrm{1}\right)^{\mathrm{2}} =\mid{x}+\mathrm{1}\mid^{\mathrm{2}} \\ $$$$\mid{x}+\mathrm{1}\mid\left(\frac{\mathrm{1}}{\mid{x}\mid}+\mathrm{1}−\frac{\mid{x}+\mathrm{1}\mid}{\mid{x}\mid}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1}\:\:\checkmark\:\:{or}\:\frac{\mathrm{1}}{\mid{x}\mid}+\mathrm{1}−\frac{\mid{x}+\mathrm{1}\mid}{\mid{x}\mid}=\mathrm{0} \\ $$$${if}\:\:{x}<−\mathrm{1}\:\Rightarrow−\frac{\mathrm{1}}{{x}}+\mathrm{1}+\left[\frac{{x}+\mathrm{1}}{{x}}=\mathrm{1}+\frac{\mathrm{1}}{{x}}\right]=\mathrm{0} \\ $$$$\mathrm{2}=\mathrm{0}\:{impossible}\: \\ $$$${if}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{0}\:\Rightarrow\:−\frac{\mathrm{1}}{{x}}+\mathrm{1}−\mathrm{1}−\frac{\mathrm{1}}{{x}}=\mathrm{0}\Rightarrow\frac{−\mathrm{2}}{{x}}=\mathrm{0} \\ $$$${again}\:{it}\:{is}\:{impossible}. \\ $$$${x}>\mathrm{0}\Rightarrow\:\frac{\mathrm{1}}{{x}}+\mathrm{1}−\mathrm{1}−\frac{\mathrm{1}}{{x}}=\mathrm{0}\:\:\checkmark\checkmark \\ $$$$\:\:{ans}\:\:\:\:\left\{−\mathrm{1}\right\}\cup\:{x}>\mathrm{0}\:\checkmark \\ $$
