Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114475 by Rio Michael last updated on 19/Sep/20

Commented by Rio Michael last updated on 19/Sep/20

suppose that two rocks are thrown from thesame point at the same moment as in the figure above. Find the distance between them as a function of time. Assume that v_0 and θ_0 are given.

$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{two}\:\mathrm{rocks}\:\mathrm{are}\:\mathrm{thrown}\:\mathrm{from} \\ $$$$\mathrm{thesame}\:\mathrm{point}\:\mathrm{at}\:\mathrm{the}\:\mathrm{same}\:\mathrm{moment}\:\mathrm{as}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{figure}\:\mathrm{above}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{them}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{time}.\:\mathrm{Assume}\:\mathrm{that} \\ $$$${v}_{\mathrm{0}} \:\mathrm{and}\:\theta_{\mathrm{0}} \:\mathrm{are}\:\mathrm{given}. \\ $$

Commented by Dwaipayan Shikari last updated on 19/Sep/20

In t_1 time A particle will cross S_y =v_0 sinθt_1 −(1/2)gt_1 ^2 (upward) B particle goes S_y ′=v_0 sinθt_1 −(1/2)gt_1 ^2 S_y −S_y ′=0 In t_1 A particle goes (v_0 cosθ_0 )t_1 toward +x direction B particle goes (v_0 cosθ_0 )t_1 in −x direction Relative distance S_x =2v_0 cosθ_0 t_1 (√(S_x ^2 +(S_y −S_y ′)^2 )) =2v_0 cosθ_0 t_1

$${In}\:{t}_{\mathrm{1}} \:{time}\:{A}\:{particle}\:{will}\:{cross}\: \\ $$$${S}_{{y}} ={v}_{\mathrm{0}} {sin}\theta{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\left({upward}\right) \\ $$$${B}\:{particle}\:{goes}\:{S}_{{y}} '={v}_{\mathrm{0}} {sin}\theta{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${S}_{{y}} −{S}_{{y}} '=\mathrm{0} \\ $$$${In}\:{t}_{\mathrm{1}} \:{A}\:{particle}\:{goes}\:\left({v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} \right){t}_{\mathrm{1}} \:\:{toward}\:+{x}\:{direction} \\ $$$${B}\:{particle}\:{goes}\:\left({v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} \right){t}_{\mathrm{1}} \:{in}\:−{x}\:{direction} \\ $$$${Relative}\:{distance}\:{S}_{{x}} =\mathrm{2}{v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} {t}_{\mathrm{1}} \\ $$$$\sqrt{{S}_{{x}} ^{\mathrm{2}} +\left({S}_{{y}} −{S}_{{y}} '\right)^{\mathrm{2}} }\:\:=\mathrm{2}{v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} {t}_{\mathrm{1}} \\ $$

Commented by Rio Michael last updated on 19/Sep/20

thanks

$$\mathrm{thanks} \\ $$

Commented by Dwaipayan Shikari last updated on 19/Sep/20

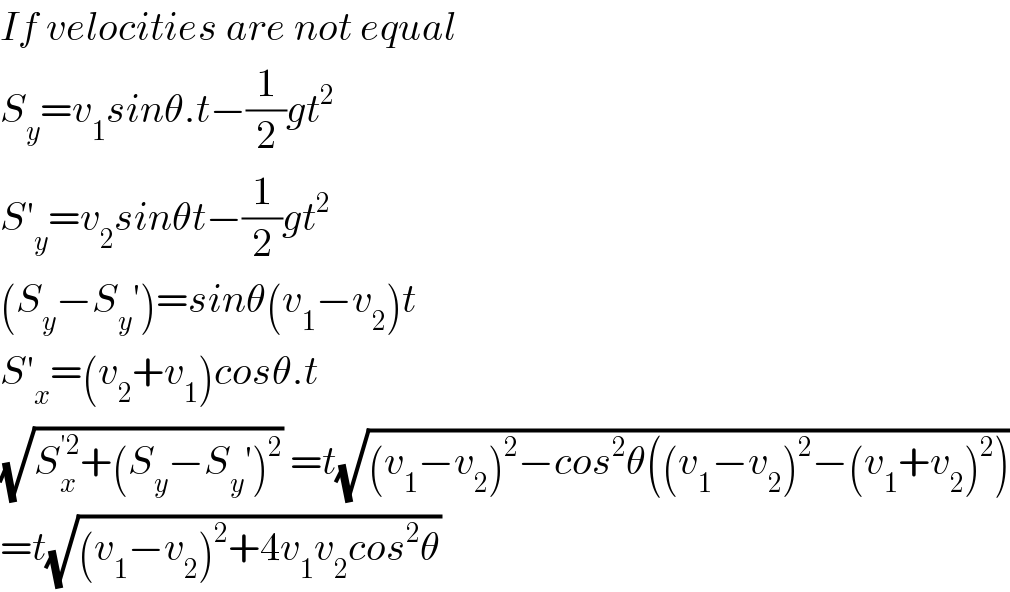
If velocities are not equal S_y =v_1 sinθ.t−(1/2)gt^2 S′_y =v_2 sinθt−(1/2)gt^2 (S_y −S_y ′)=sinθ(v_1 −v_2 )t S′_x =(v_2 +v_1 )cosθ.t (√(S_x ^(′2) +(S_y −S_y ′)^2 )) =t(√((v_1 −v_2 )^2 −cos^2 θ((v_1 −v_2 )^2 −(v_1 +v_2 )^2 ))) =t(√((v_1 −v_2 )^2 +4v_1 v_2 cos^2 θ))

$${If}\:{velocities}\:{are}\:{not}\:{equal} \\ $$$${S}_{{y}} ={v}_{\mathrm{1}} {sin}\theta.{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${S}'_{{y}} ={v}_{\mathrm{2}} {sin}\theta{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\left({S}_{{y}} −{S}_{{y}} '\right)={sin}\theta\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right){t} \\ $$$${S}'_{{x}} =\left({v}_{\mathrm{2}} +{v}_{\mathrm{1}} \right){cos}\theta.{t} \\ $$$$\sqrt{{S}_{{x}} ^{'\mathrm{2}} +\left({S}_{{y}} −{S}_{{y}} '\right)^{\mathrm{2}} }\:={t}\sqrt{\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} −{cos}^{\mathrm{2}} \theta\left(\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} −\left({v}_{\mathrm{1}} +{v}_{\mathrm{2}} \right)^{\mathrm{2}} \right)} \\ $$$$={t}\sqrt{\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{v}_{\mathrm{1}} {v}_{\mathrm{2}} {cos}^{\mathrm{2}} \theta} \\ $$

Commented by Rio Michael last updated on 19/Sep/20

thanks for the extra

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{extra} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com