
Question Number 114577 by Khalmohmmad last updated on 19/Sep/20
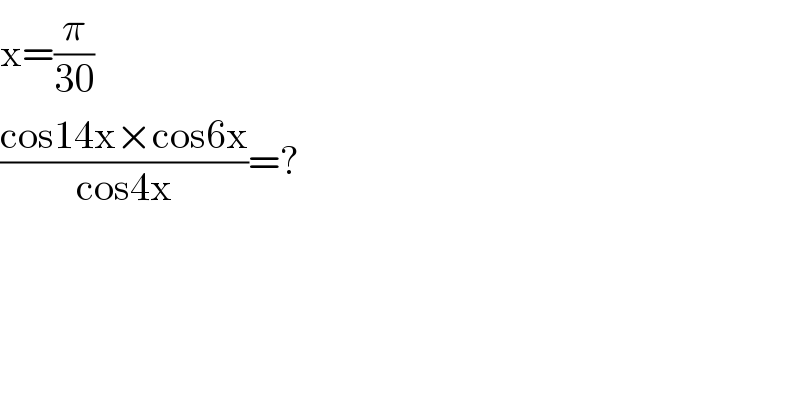
$$\mathrm{x}=\frac{\pi}{\mathrm{30}} \\ $$$$\frac{\mathrm{cos14x}×\mathrm{cos6x}}{\mathrm{cos4x}}=? \\ $$
Commented by bemath last updated on 19/Sep/20
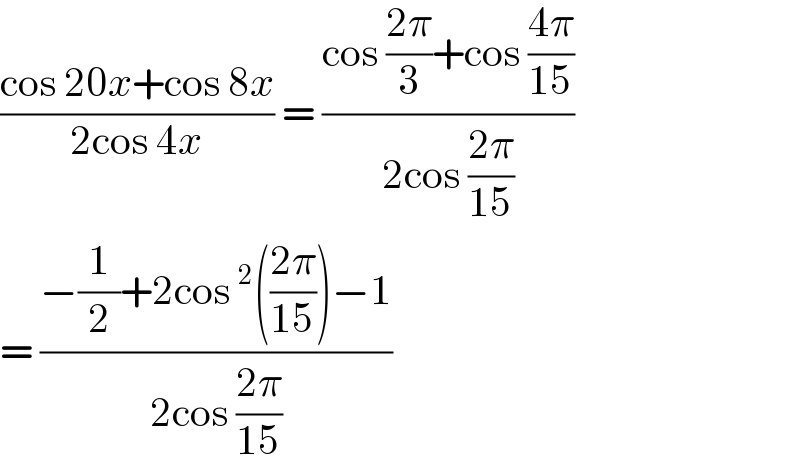
$$\frac{\mathrm{cos}\:\mathrm{20}{x}+\mathrm{cos}\:\mathrm{8}{x}}{\mathrm{2cos}\:\mathrm{4}{x}}\:=\:\frac{\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}}{\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}} \\ $$$$=\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{15}}\right)−\mathrm{1}}{\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}} \\ $$
Commented by MJS_new last updated on 19/Sep/20

$$\mathrm{we}\:\mathrm{can}\:\mathrm{express}\:\mathrm{this}\:\mathrm{with}\:\mathrm{roots}\:\mathrm{but}\:\mathrm{I}\:\mathrm{haven}'\mathrm{t} \\ $$$$\mathrm{got}\:\mathrm{the}\:\mathrm{time}\:\mathrm{right}\:\mathrm{now} \\ $$
Commented by MJS_new last updated on 20/Sep/20
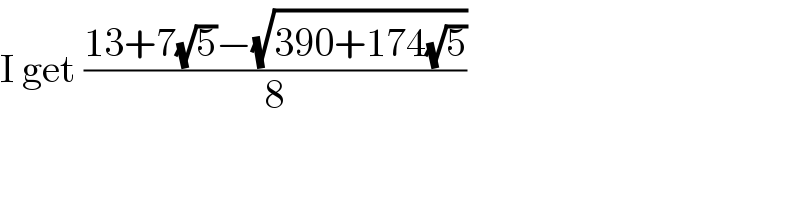
$$\mathrm{I}\:\mathrm{get}\:\frac{\mathrm{13}+\mathrm{7}\sqrt{\mathrm{5}}−\sqrt{\mathrm{390}+\mathrm{174}\sqrt{\mathrm{5}}}}{\mathrm{8}} \\ $$
Commented by bobhans last updated on 20/Sep/20

$${how}\:{sir}? \\ $$
Commented by MJS_new last updated on 20/Sep/20
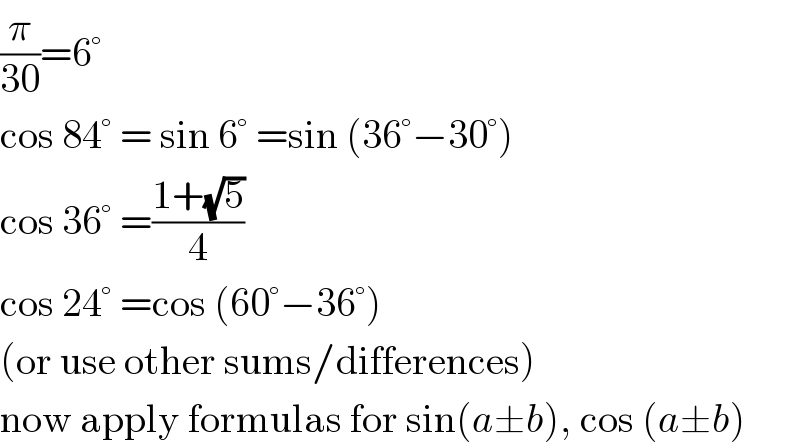
$$\frac{\pi}{\mathrm{30}}=\mathrm{6}° \\ $$$$\mathrm{cos}\:\mathrm{84}°\:=\:\mathrm{sin}\:\mathrm{6}°\:=\mathrm{sin}\:\left(\mathrm{36}°−\mathrm{30}°\right) \\ $$$$\mathrm{cos}\:\mathrm{36}°\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\mathrm{24}°\:=\mathrm{cos}\:\left(\mathrm{60}°−\mathrm{36}°\right) \\ $$$$\left(\mathrm{or}\:\mathrm{use}\:\mathrm{other}\:\mathrm{sums}/\mathrm{differences}\right) \\ $$$$\mathrm{now}\:\mathrm{apply}\:\mathrm{formulas}\:\mathrm{for}\:\mathrm{sin}\left({a}\pm{b}\right),\:\mathrm{cos}\:\left({a}\pm{b}\right) \\ $$
Answered by 1549442205PVT last updated on 20/Sep/20
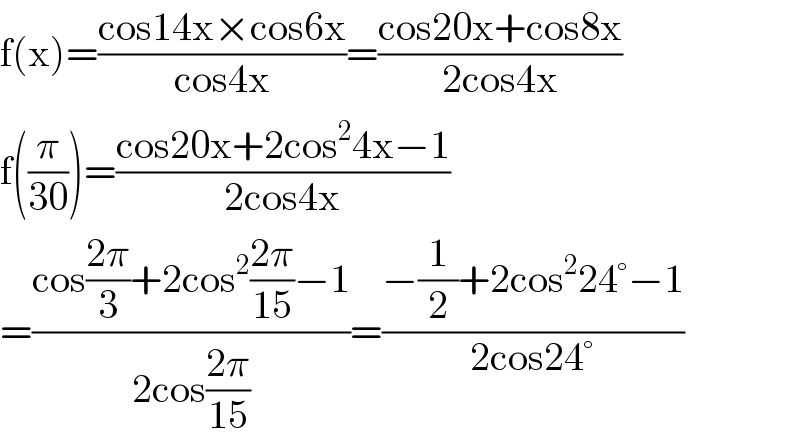
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos14x}×\mathrm{cos6x}}{\mathrm{cos4x}}=\frac{\mathrm{cos20x}+\mathrm{cos8x}}{\mathrm{2cos4x}}\: \\ $$$$\mathrm{f}\left(\frac{\pi}{\mathrm{30}}\right)=\frac{\mathrm{cos20x}+\mathrm{2cos}^{\mathrm{2}} \mathrm{4x}−\mathrm{1}}{\mathrm{2cos4x}} \\ $$$$=\frac{\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2cos}^{\mathrm{2}} \frac{\mathrm{2}\pi}{\mathrm{15}}−\mathrm{1}}{\mathrm{2cos}\frac{\mathrm{2}\pi}{\mathrm{15}}}=\frac{−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2cos}^{\mathrm{2}} \mathrm{24}°−\mathrm{1}}{\mathrm{2cos24}°} \\ $$
