Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 114597 by O Predador last updated on 19/Sep/20

What is the number value of f[((log((( (√(x )) − 1 )/(x − 1))) ))^(1/3) ] = (√((√(x )) + x )) for f(−1)? a) 0,1 b) 27 c) 81 d) 10 e) 12

$$\: \\ $$$$\:\:\:\boldsymbol{\mathrm{What}}\:\:\boldsymbol{\mathrm{is}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{number}}\:\:\boldsymbol{\mathrm{value}}\:\:\boldsymbol{\mathrm{of}}\:\:\:\boldsymbol{\mathrm{f}}\left[\sqrt[{\mathrm{3}}]{\boldsymbol{\mathrm{log}}\left(\frac{\:\sqrt{\boldsymbol{\mathrm{x}}\:\:}\:−\:\:\:\mathrm{1}\:}{\boldsymbol{\mathrm{x}}\:\:\:−\:\:\:\mathrm{1}}\right)\:\:}\right]\:\:=\:\:\sqrt{\sqrt{\boldsymbol{\mathrm{x}}\:}\:\:\:+\:\:\:\boldsymbol{\mathrm{x}}\:}\:\:\boldsymbol{\mathrm{for}}\:\:\boldsymbol{\mathrm{f}}\left(−\mathrm{1}\right)? \\ $$$$\: \\ $$$$\left.\:\:\:\boldsymbol{\mathrm{a}}\right)\:\mathrm{0},\mathrm{1} \\ $$$$\left.\:\:\:\boldsymbol{\mathrm{b}}\right)\:\mathrm{27} \\ $$$$\left.\:\:\:\boldsymbol{\mathrm{c}}\right)\:\mathrm{81} \\ $$$$\left.\:\:\:\boldsymbol{\mathrm{d}}\right)\:\mathrm{10} \\ $$$$\left.\:\:\:\boldsymbol{\mathrm{e}}\right)\:\mathrm{12} \\ $$$$\: \\ $$

Answered by Olaf last updated on 19/Sep/20

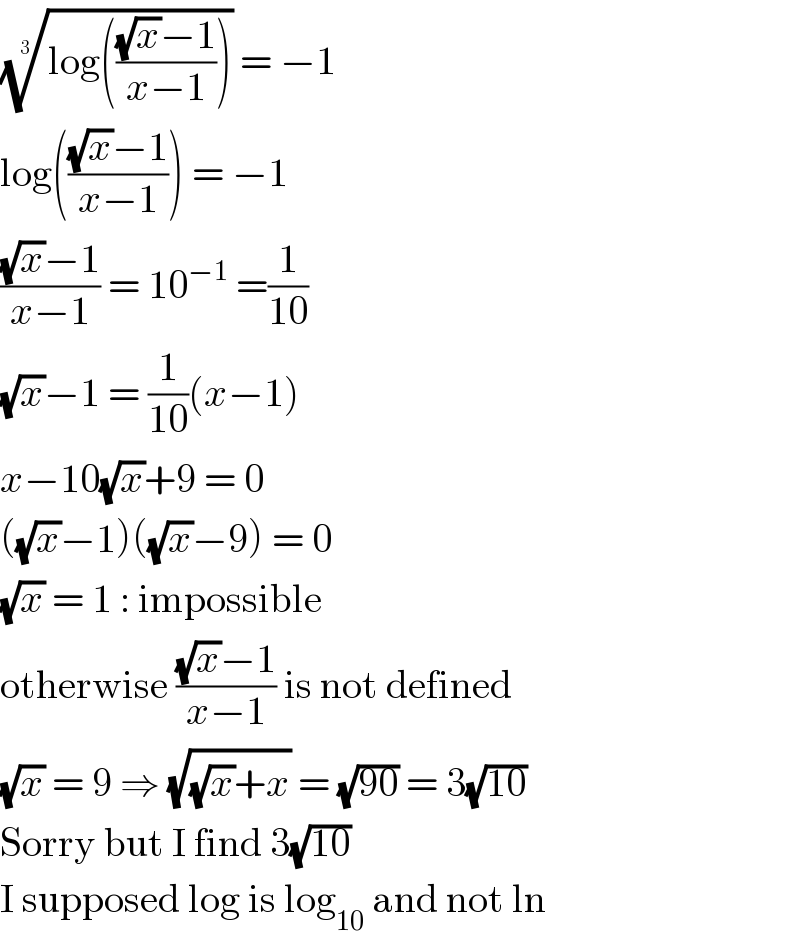
((log((((√x)−1)/(x−1)))))^(1/3) = −1 log((((√x)−1)/(x−1))) = −1 (((√x)−1)/(x−1)) = 10^(−1) =(1/(10)) (√x)−1 = (1/(10))(x−1) x−10(√x)+9 = 0 ((√x)−1)((√x)−9) = 0 (√x) = 1 : impossible otherwise (((√x)−1)/(x−1)) is not defined (√x) = 9 ⇒ (√((√x)+x)) = (√(90)) = 3(√(10)) Sorry but I find 3(√(10)) I supposed log is log_(10) and not ln

$$\sqrt[{\mathrm{3}}]{\mathrm{log}\left(\frac{\sqrt{{x}}−\mathrm{1}}{{x}−\mathrm{1}}\right)}\:=\:−\mathrm{1} \\ $$$$\mathrm{log}\left(\frac{\sqrt{{x}}−\mathrm{1}}{{x}−\mathrm{1}}\right)\:=\:−\mathrm{1} \\ $$$$\frac{\sqrt{{x}}−\mathrm{1}}{{x}−\mathrm{1}}\:=\:\mathrm{10}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\sqrt{{x}}−\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{10}}\left({x}−\mathrm{1}\right) \\ $$$${x}−\mathrm{10}\sqrt{{x}}+\mathrm{9}\:=\:\mathrm{0} \\ $$$$\left(\sqrt{{x}}−\mathrm{1}\right)\left(\sqrt{{x}}−\mathrm{9}\right)\:=\:\mathrm{0} \\ $$$$\sqrt{{x}}\:=\:\mathrm{1}\::\:\mathrm{impossible} \\ $$$$\mathrm{otherwise}\:\frac{\sqrt{{x}}−\mathrm{1}}{{x}−\mathrm{1}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\sqrt{{x}}\:=\:\mathrm{9}\:\Rightarrow\:\sqrt{\sqrt{{x}}+{x}}\:=\:\sqrt{\mathrm{90}}\:=\:\mathrm{3}\sqrt{\mathrm{10}} \\ $$$$\mathrm{Sorry}\:\mathrm{but}\:\mathrm{I}\:\mathrm{find}\:\mathrm{3}\sqrt{\mathrm{10}} \\ $$$$\mathrm{I}\:\mathrm{supposed}\:\mathrm{log}\:\mathrm{is}\:\mathrm{log}_{\mathrm{10}} \:\mathrm{and}\:\mathrm{not}\:\mathrm{ln} \\ $$

Commented by O Predador last updated on 20/Sep/20

Thank you!

$$\:\mathrm{Thank}\:\mathrm{you}! \\ $$

Answered by floor(10²Eta[1]) last updated on 20/Sep/20

f(((log((((√x)−1)/(x−1)))))^(1/3) )=(√((√x)+x)) ((log((((√x)−1)/(x−1)))))^(1/3) =−1⇒log((((√x)−1)/(x−1)))=−1 (((√x)−1)/(x−1))=10^(−1) =(1/(10))⇒10(√x)−10=x−1 10(√x)=x+9 100x=x^2 +18x+81 x^2 −82x+81=0 x=((82±80)/2)⇒x=1 or 81⇒x=81 (because x≠1) x=81⇒ f(−1)=(√((√(81))+81))=(√(90)) now if log is ln the logic is the same and the answer is (√(e^2 −e))

$$\mathrm{f}\left(\sqrt[{\mathrm{3}}]{\mathrm{log}\left(\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)}\right)=\sqrt{\sqrt{\mathrm{x}}+\mathrm{x}} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{log}\left(\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)}=−\mathrm{1}\Rightarrow\mathrm{log}\left(\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)=−\mathrm{1} \\ $$$$\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\mathrm{x}−\mathrm{1}}=\mathrm{10}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{10}}\Rightarrow\mathrm{10}\sqrt{\mathrm{x}}−\mathrm{10}=\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{10}\sqrt{\mathrm{x}}=\mathrm{x}+\mathrm{9} \\ $$$$\mathrm{100x}=\mathrm{x}^{\mathrm{2}} +\mathrm{18x}+\mathrm{81} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{82x}+\mathrm{81}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{\mathrm{82}\pm\mathrm{80}}{\mathrm{2}}\Rightarrow\mathrm{x}=\mathrm{1}\:\mathrm{or}\:\mathrm{81}\Rightarrow\mathrm{x}=\mathrm{81}\:\left(\mathrm{because}\:\mathrm{x}\neq\mathrm{1}\right) \\ $$$$\mathrm{x}=\mathrm{81}\Rightarrow \\ $$$$\mathrm{f}\left(−\mathrm{1}\right)=\sqrt{\sqrt{\mathrm{81}}+\mathrm{81}}=\sqrt{\mathrm{90}} \\ $$$$\mathrm{now}\:\mathrm{if}\:\mathrm{log}\:\mathrm{is}\:\mathrm{ln}\:\mathrm{the}\:\mathrm{logic}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{e}^{\mathrm{2}} −\mathrm{e}} \\ $$$$ \\ $$

Answered by 1549442205PVT last updated on 20/Sep/20

We need find x>0, x ≠1such that log(((√x)−1)/(x−1))=−1⇔log(((√x)−1)/(((√x)−1)((√x)+1)))=−1 ⇔log(1/( (√x)+1))=−1⇔−log((√x)+1)=−1 •If logx=log_(10) x then ⇔log((√x)+1)=1⇒(√x)+1=10 ⇔(√x)=9⇔x=81 ⇒f(−1)=(√(9+81))=(√(90)) •If logx = lnx then (√x)+1=e⇒(√x)=e−1 ⇒x=e^2 −2e+1⇒f(−1)=(√( e^2 −e)) Available answer is false!

$$\mathrm{We}\:\mathrm{need}\:\mathrm{find}\:\mathrm{x}>\mathrm{0},\:\mathrm{x}\:\neq\mathrm{1such}\:\mathrm{that}\: \\ $$$$\mathrm{log}\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\mathrm{x}−\mathrm{1}}=−\mathrm{1}\Leftrightarrow\mathrm{log}\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\left(\sqrt{\mathrm{x}}−\mathrm{1}\right)\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)}=−\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{log}\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}+\mathrm{1}}=−\mathrm{1}\Leftrightarrow−\mathrm{log}\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)=−\mathrm{1} \\ $$$$\bullet\mathrm{If}\:\mathrm{logx}=\mathrm{log}_{\mathrm{10}} \mathrm{x}\:\mathrm{then} \\ $$$$\Leftrightarrow\mathrm{log}\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)=\mathrm{1}\Rightarrow\sqrt{\mathrm{x}}+\mathrm{1}=\mathrm{10} \\ $$$$\Leftrightarrow\sqrt{\mathrm{x}}=\mathrm{9}\Leftrightarrow\mathrm{x}=\mathrm{81} \\ $$$$\Rightarrow\mathrm{f}\left(−\mathrm{1}\right)=\sqrt{\mathrm{9}+\mathrm{81}}=\sqrt{\mathrm{90}} \\ $$$$\bullet\mathrm{If}\:\mathrm{logx}\:=\:\mathrm{lnx}\:\mathrm{then}\:\sqrt{\mathrm{x}}+\mathrm{1}=\mathrm{e}\Rightarrow\sqrt{\mathrm{x}}=\mathrm{e}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{e}^{\mathrm{2}} −\mathrm{2e}+\mathrm{1}\Rightarrow\mathrm{f}\left(−\mathrm{1}\right)=\sqrt{\:\mathrm{e}^{\mathrm{2}} −\mathrm{e}} \\ $$$$\boldsymbol{\mathrm{Available}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{false}}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com