Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 114627 by john santu last updated on 20/Sep/20

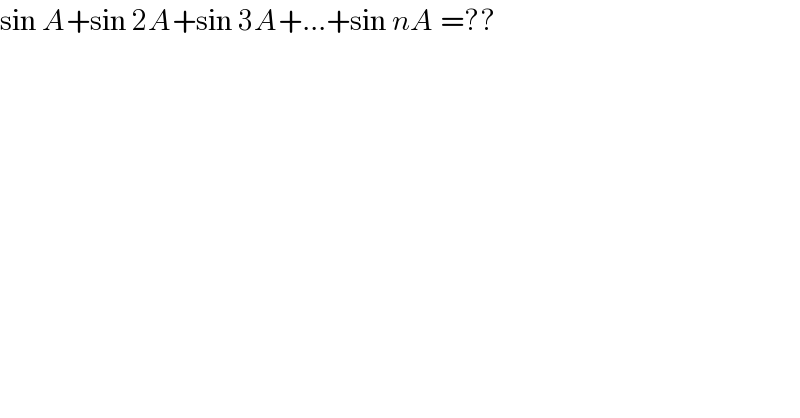
sin A+sin 2A+sin 3A+...+sin nA =??

$$\mathrm{sin}\:{A}+\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{3}{A}+...+\mathrm{sin}\:{nA}\:=?? \\ $$

Answered by mathmax by abdo last updated on 20/Sep/20

let S_n (x) =sinx +sin(2x)+...+sin(nx)=Σ_(k=0) ^n sin(kx) =Im(Σ_(k=0) ^n e^(ikx) ) we have Σ_(k=0) ^n e^(ikx) =Σ_(k=0) ^n (e^(ix) )^k =((1−(e^(ix) )^(n+1) )/(1−e^(ix) )) =((1−cos(n+1)x−isin(n+1)x)/(1−cosx −isinx)) =((2sin^2 (n+1)(x/2)−2i sin((n+1)(x/2))cos(n+1)(x/2))/(2sin^2 ((x/2))−2isin((x/2))cos((x/2)))) =((−isin(n+1)(x/2){ e^(i(n+1)(x/2)) })/(−isin((x/2))e^((ix)/2) )) =((sin((n+1)(x/2)))/(sin((x/2))))×e^(in(x/2)) =((sin((((n+1)x)/2)))/(sin((x/2))))×{cos(((nx)/2))+isin(((nx)/2))} ⇒ S_n (x) =((sin(((nx)/2))sin((((n+1)x)/2)))/(sin((x/2)))) (x≠2kπ )

$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\mathrm{sinx}\:+\mathrm{sin}\left(\mathrm{2x}\right)+...+\mathrm{sin}\left(\mathrm{nx}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{sin}\left(\mathrm{kx}\right) \\ $$$$=\mathrm{Im}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{e}^{\mathrm{ikx}} \right)\:\:\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{e}^{\mathrm{ikx}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \:=\frac{\mathrm{1}−\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{e}^{\mathrm{ix}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}−\mathrm{isin}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}}{\mathrm{1}−\mathrm{cosx}\:−\mathrm{isinx}} \\ $$$$=\frac{\mathrm{2sin}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{2i}\:\mathrm{sin}\left(\left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{−\mathrm{isin}\left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}\left\{\:\mathrm{e}^{\mathrm{i}\left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}} \right\}}{−\mathrm{isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{e}^{\frac{\mathrm{ix}}{\mathrm{2}}} }\:=\frac{\mathrm{sin}\left(\left(\mathrm{n}+\mathrm{1}\right)\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}×\mathrm{e}^{\mathrm{in}\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}×\left\{\mathrm{cos}\left(\frac{\mathrm{nx}}{\mathrm{2}}\right)+\mathrm{isin}\left(\frac{\mathrm{nx}}{\mathrm{2}}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\frac{\mathrm{sin}\left(\frac{\mathrm{nx}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:\:\:\:\left(\mathrm{x}\neq\mathrm{2k}\pi\:\:\:\right) \\ $$

Answered by Dwaipayan Shikari last updated on 20/Sep/20

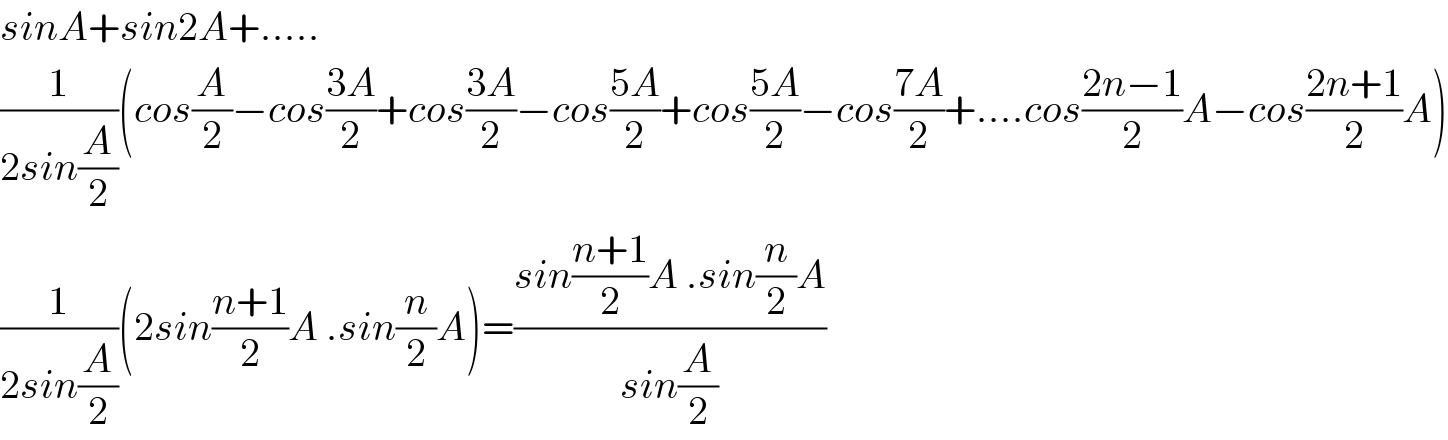
sinA+sin2A+..... (1/(2sin(A/2)))(cos(A/2)−cos((3A)/2)+cos((3A)/2)−cos((5A)/2)+cos((5A)/2)−cos((7A)/2)+....cos((2n−1)/2)A−cos((2n+1)/2)A) (1/(2sin(A/2)))(2sin((n+1)/2)A .sin(n/2)A)=((sin((n+1)/2)A .sin(n/2)A)/(sin(A/2)))

$${sinA}+{sin}\mathrm{2}{A}+..... \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}}\left({cos}\frac{{A}}{\mathrm{2}}−{cos}\frac{\mathrm{3}{A}}{\mathrm{2}}+{cos}\frac{\mathrm{3}{A}}{\mathrm{2}}−{cos}\frac{\mathrm{5}{A}}{\mathrm{2}}+{cos}\frac{\mathrm{5}{A}}{\mathrm{2}}−{cos}\frac{\mathrm{7}{A}}{\mathrm{2}}+....{cos}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}{A}−{cos}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{A}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}}\left(\mathrm{2}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{A}\:.{sin}\frac{{n}}{\mathrm{2}}{A}\right)=\frac{{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{A}\:.{sin}\frac{{n}}{\mathrm{2}}{A}}{{sin}\frac{{A}}{\mathrm{2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com