
Question Number 114671 by soumyasaha last updated on 20/Sep/20
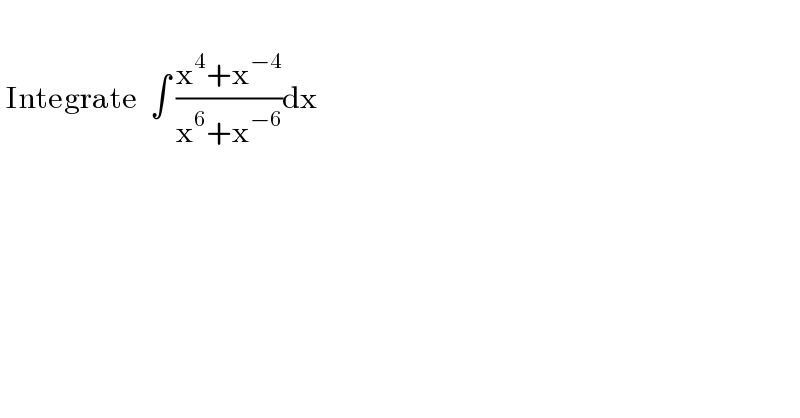
$$ \\ $$$$\:\mathrm{Integrate}\:\:\int\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{−\mathrm{4}} }{\mathrm{x}^{\mathrm{6}} +\mathrm{x}^{−\mathrm{6}} }\mathrm{dx} \\ $$
Answered by Olaf last updated on 20/Sep/20
![∫((x^(10) +x^2 )/(x^(12) +1))dx x^(12) +1 = 0 ⇔ x^(12) = −1 = e^(iπ) x_k = e^(i((π/(12))+((kπ)/6))) , k = 0,1,2...11 ∫Σ_(k=0) ^(11) (A_k /(x−x_k ))dx A_k = ((x_k ^6 (x_k ^4 +x_k ^(−4) ))/(Π_(j=0_(j≠k) ) ^(11) (x_j −x_k ))) x_k ^6 = e^(i((π/(12))+((kπ)/6))×6) = e^(i((π/2)+kπ) = (−1)^k i) x_k ^4 +x_k ^(−4) = 2cos[((π/(12))+((kπ)/6))×4] = 2cos((π/3)+((2kπ)/3)) x_k ^4 +x_k ^(−4) = 0 if k = 1,4,7,10 x_j −x_k = e^(i((π/(12))+((jπ)/6))) −e^(i((π/(12))+((kπ)/6))) x_j −x_k = e^(i((π/(12))+(((j+k)π)/(12)))) [e^(i(((j−k)π)/(12))) −e^(−i(((j−k)π)/(12))) ] x_j −x_k = 2ie^(i((π/(12))+(((j+k)π)/(12)))) sin[(((j−k)π)/(12))] A_k = (((−1)^k i×2cos((π/3)+((2kπ)/3)))/(2ie^(i((π/(12))+(((j+k)π)/(12)))) sin[(((j−k)π)/(12))])) A_k = (((−1)^k cos((π/3)+((2kπ)/3)))/(sin[(((j−k)π)/(12))]))e^(−i((π/(12))+(((j+k)π)/(12)))) ∫((x^4 +x^(−4) )/(x^6 +x^(−6) ))dx = Σ_(k=0,2,3,5,6,8,9,11) A_k ln∣x−x_k ∣](Q114677.png)
$$\int\frac{{x}^{\mathrm{10}} +{x}^{\mathrm{2}} }{{x}^{\mathrm{12}} +\mathrm{1}}{dx} \\ $$$${x}^{\mathrm{12}} +\mathrm{1}\:=\:\mathrm{0}\:\Leftrightarrow\:{x}^{\mathrm{12}} \:=\:−\mathrm{1}\:=\:{e}^{{i}\pi} \\ $$$${x}_{{k}} \:=\:{e}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{{k}\pi}{\mathrm{6}}\right)} ,\:{k}\:=\:\mathrm{0},\mathrm{1},\mathrm{2}...\mathrm{11} \\ $$$$\int\underset{{k}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}\frac{\mathrm{A}_{{k}} }{{x}−{x}_{{k}} }{dx} \\ $$$$\mathrm{A}_{{k}} \:=\:\frac{{x}_{{k}} ^{\mathrm{6}} \left({x}_{{k}} ^{\mathrm{4}} +{x}_{{k}} ^{−\mathrm{4}} \right)}{\underset{\underset{{j}\neq{k}} {{j}=\mathrm{0}}} {\overset{\mathrm{11}} {\prod}}\left({x}_{{j}} −{x}_{{k}} \right)} \\ $$$${x}_{{k}} ^{\mathrm{6}} =\:{e}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{{k}\pi}{\mathrm{6}}\right)×\mathrm{6}} \:=\:{e}^{{i}\left(\frac{\pi}{\mathrm{2}}+{k}\pi\right)\:=\:\left(−\mathrm{1}\right)^{{k}} {i}} \\ $$$${x}_{{k}} ^{\mathrm{4}} +{x}_{{k}} ^{−\mathrm{4}} \:=\:\mathrm{2cos}\left[\left(\frac{\pi}{\mathrm{12}}+\frac{{k}\pi}{\mathrm{6}}\right)×\mathrm{4}\right]\:=\:\mathrm{2cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$${x}_{{k}} ^{\mathrm{4}} +{x}_{{k}} ^{−\mathrm{4}} \:=\:\mathrm{0}\:\mathrm{if}\:{k}\:=\:\mathrm{1},\mathrm{4},\mathrm{7},\mathrm{10} \\ $$$${x}_{{j}} −{x}_{{k}} \:=\:{e}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{{j}\pi}{\mathrm{6}}\right)} −{e}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{{k}\pi}{\mathrm{6}}\right)} \\ $$$${x}_{{j}} −{x}_{{k}} \:=\:{e}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{\left({j}+{k}\right)\pi}{\mathrm{12}}\right)} \left[{e}^{{i}\frac{\left({j}−{k}\right)\pi}{\mathrm{12}}} −{e}^{−{i}\frac{\left({j}−{k}\right)\pi}{\mathrm{12}}} \right] \\ $$$${x}_{{j}} −{x}_{{k}} \:=\:\mathrm{2}{ie}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{\left({j}+{k}\right)\pi}{\mathrm{12}}\right)} \mathrm{sin}\left[\frac{\left({j}−{k}\right)\pi}{\mathrm{12}}\right] \\ $$$$\mathrm{A}_{{k}} \:=\:\frac{\left(−\mathrm{1}\right)^{{k}} {i}×\mathrm{2cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)}{\mathrm{2}{ie}^{{i}\left(\frac{\pi}{\mathrm{12}}+\frac{\left({j}+{k}\right)\pi}{\mathrm{12}}\right)} \mathrm{sin}\left[\frac{\left({j}−{k}\right)\pi}{\mathrm{12}}\right]} \\ $$$$\mathrm{A}_{{k}} \:=\:\frac{\left(−\mathrm{1}\right)^{{k}} \mathrm{cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)}{\mathrm{sin}\left[\frac{\left({j}−{k}\right)\pi}{\mathrm{12}}\right]}{e}^{−{i}\left(\frac{\pi}{\mathrm{12}}+\frac{\left({j}+{k}\right)\pi}{\mathrm{12}}\right)} \\ $$$$\int\frac{{x}^{\mathrm{4}} +{x}^{−\mathrm{4}} }{{x}^{\mathrm{6}} +{x}^{−\mathrm{6}} }{dx}\:=\:\underset{{k}=\mathrm{0},\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{6},\mathrm{8},\mathrm{9},\mathrm{11}} {\sum}\mathrm{A}_{{k}} \mathrm{ln}\mid{x}−{x}_{{k}} \mid \\ $$$$ \\ $$
Commented by soumyasaha last updated on 20/Sep/20

$$\mathrm{Thanks}\:\mathrm{Sir}. \\ $$
