Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114689 by arkanmath7@gmail.com last updated on 20/Sep/20

∫xsin^n xdx

$$\int{xsin}^{{n}} {xdx} \\ $$

Answered by 1549442205PVT last updated on 20/Sep/20

Just give out reduction formula: Integrating by parts we get: I_n =∫xsin^n xdx=∫xsin^(n−1) x.sinxdx =−xsin^(n−1) (x)cosx+∫cosx{sin^(n−1) x+x(n−1)sin^(n−2) xcosx}dx =−xcosxsin^(n−1) x+∫sin^(n−1) xcosxdx +(n−1)∫xsin^(n−2) x(1−sin^2 x)dx =−xcosxsin^(n−1) x+((sin^n x)/n)+(n−1)(I_(n−2) −I_n ) ⇒(1+(n−1)I_n =−xcosxsin^(n−1) x+((sin^n x)/n) +(n−1)I_(n−2) ⇒I_n =((−xcosxsin^(n−1) x)/n)+((sin^n x)/n^2 )+((n−1)/n)I_(n−2)

$$\mathrm{Just}\:\mathrm{give}\:\mathrm{out}\:\mathrm{reduction}\:\mathrm{formula}: \\ $$$$\mathrm{Integrating}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{I}_{\mathrm{n}} =\int{xsin}^{{n}} {xdx}=\int\mathrm{xsin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}.\mathrm{sinxdx} \\ $$$$=−\mathrm{xsin}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}\right)\mathrm{cosx}+\int\mathrm{cosx}\left\{\mathrm{sin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}+\mathrm{x}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{sin}^{\mathrm{n}−\mathrm{2}} \mathrm{xcosx}\right\}\mathrm{dx} \\ $$$$=−\mathrm{xcosxsin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}+\int\mathrm{sin}^{\mathrm{n}−\mathrm{1}} \mathrm{xcosxdx} \\ $$$$+\left(\mathrm{n}−\mathrm{1}\right)\int\mathrm{xsin}^{\mathrm{n}−\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx} \\ $$$$=−\mathrm{xcosxsin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}+\frac{\mathrm{sin}^{\mathrm{n}} \mathrm{x}}{\mathrm{n}}+\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{I}_{\mathrm{n}−\mathrm{2}} −\mathrm{I}_{\mathrm{n}} \right) \\ $$$$\Rightarrow\left(\mathrm{1}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}} =−\mathrm{xcosxsin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}+\frac{\mathrm{sin}^{\mathrm{n}} \mathrm{x}}{\mathrm{n}}\right. \\ $$$$+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{I}_{\mathrm{n}} =\frac{−\mathrm{xcosxsin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}}{\mathrm{n}}+\frac{\mathrm{sin}^{\mathrm{n}} \mathrm{x}}{\mathrm{n}^{\mathrm{2}} }+\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}}\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$

Commented by arkanmath7@gmail.com last updated on 20/Sep/20

I solved it in same way but I stopped at I_(n−2) . Is it true to let it as it is?

$${I}\:{solved}\:{it}\:{in}\:{same}\:{way}\:{but}\:{I}\:{stopped}\:{at} \\ $$$${I}_{{n}−\mathrm{2}} .\:{Is}\:{it}\:{true}\:{to}\:{let}\:{it}\:{as}\:{it}\:{is}? \\ $$

Commented by 1549442205PVT last updated on 20/Sep/20

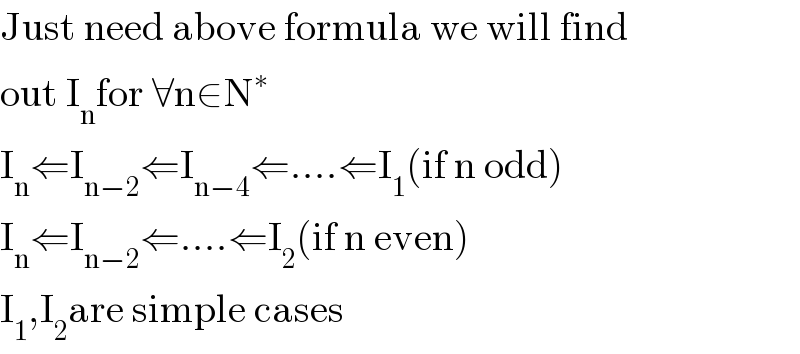
Just need above formula we will find out I_n for ∀n∈N^∗ I_n ⇐I_(n−2) ⇐I_(n−4) ⇐....⇐I_1 (if n odd) I_n ⇐I_(n−2) ⇐....⇐I_2 (if n even) I_1 ,I_2 are simple cases

$$\mathrm{Just}\:\mathrm{need}\:\mathrm{above}\:\mathrm{formula}\:\mathrm{we}\:\mathrm{will}\:\mathrm{find} \\ $$$$\mathrm{out}\:\mathrm{I}_{\mathrm{n}} \mathrm{for}\:\forall\mathrm{n}\in\mathrm{N}^{\ast} \\ $$$$\mathrm{I}_{\mathrm{n}} \Leftarrow\mathrm{I}_{\mathrm{n}−\mathrm{2}} \Leftarrow\mathrm{I}_{\mathrm{n}−\mathrm{4}} \Leftarrow....\Leftarrow\mathrm{I}_{\mathrm{1}} \left(\mathrm{if}\:\mathrm{n}\:\mathrm{odd}\right) \\ $$$$\mathrm{I}_{\mathrm{n}} \Leftarrow\mathrm{I}_{\mathrm{n}−\mathrm{2}} \Leftarrow....\Leftarrow\mathrm{I}_{\mathrm{2}} \left(\mathrm{if}\:\mathrm{n}\:\mathrm{even}\right) \\ $$$$\mathrm{I}_{\mathrm{1}} ,\mathrm{I}_{\mathrm{2}} \mathrm{are}\:\mathrm{simple}\:\mathrm{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com