
Question Number 1147 by prakash jain last updated on 04/Jul/15
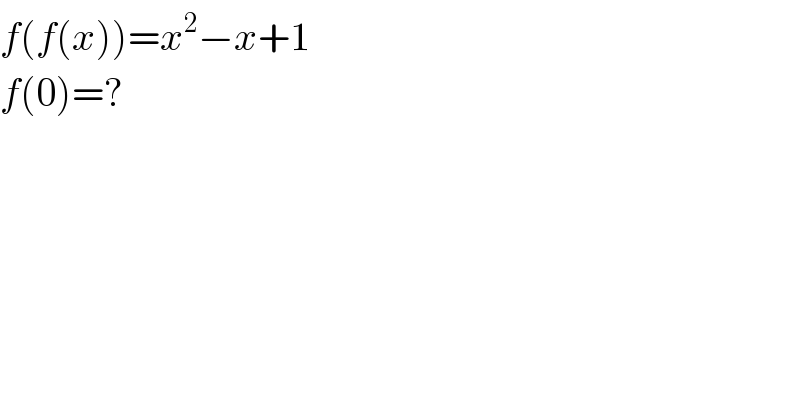
$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=? \\ $$
Commented by prakash jain last updated on 04/Jul/15

$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1} \\ $$
Commented by 123456 last updated on 04/Jul/15
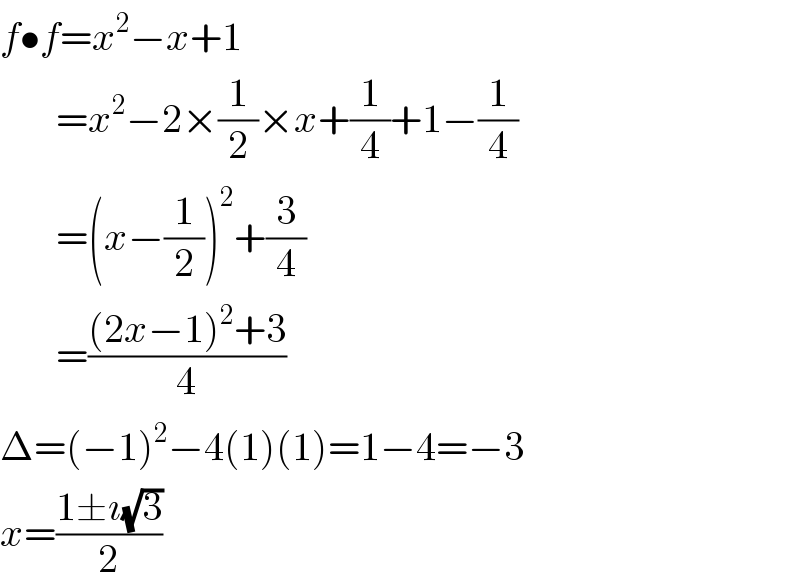
$${f}\bullet{f}={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:={x}^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×{x}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:=\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}} \\ $$$$\Delta=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{4}=−\mathrm{3} \\ $$$${x}=\frac{\mathrm{1}\pm\imath\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by 123456 last updated on 04/Jul/15
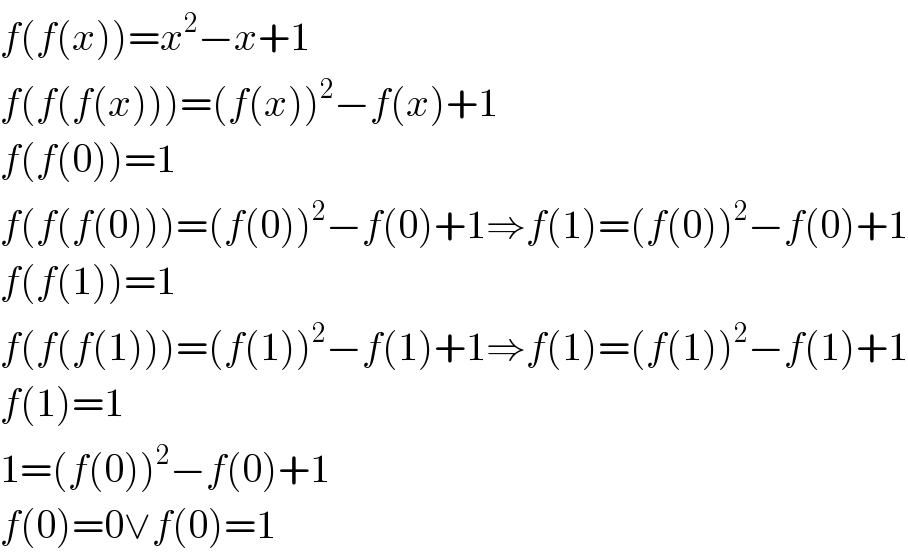
$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)=\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1} \\ $$$${f}\left({f}\left({f}\left(\mathrm{0}\right)\right)\right)=\left({f}\left(\mathrm{0}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{1}\right)=\left({f}\left(\mathrm{0}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${f}\left({f}\left(\mathrm{1}\right)\right)=\mathrm{1} \\ $$$${f}\left({f}\left({f}\left(\mathrm{1}\right)\right)\right)=\left({f}\left(\mathrm{1}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{1}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{1}\right)=\left({f}\left(\mathrm{1}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{1}=\left({f}\left(\mathrm{0}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\vee{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$
Commented by prakash jain last updated on 05/Jul/15
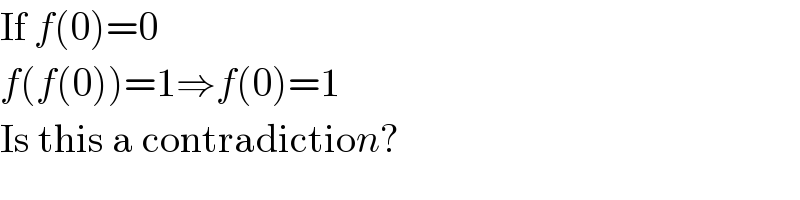
$$\mathrm{If}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1}\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{Is}\:\mathrm{this}\:\mathrm{a}\:\mathrm{contradictio}{n}? \\ $$
Commented by 123456 last updated on 05/Jul/15

$$\left.\mathrm{yes}\::\right) \\ $$$$\mathrm{then}\:{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$
Commented by prakash jain last updated on 16/Jul/15
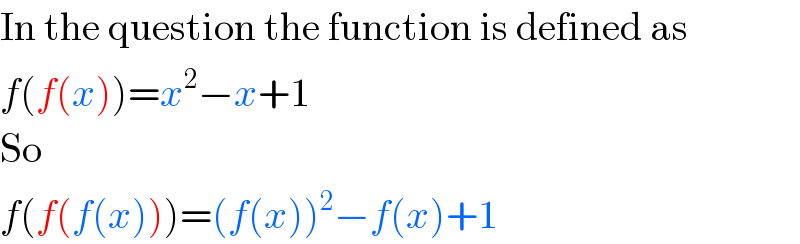
$$\mathrm{In}\:\mathrm{the}\:\mathrm{question}\:\mathrm{the}\:\mathrm{function}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as} \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$\mathrm{So} \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)=\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 12/Aug/15

$${Dear}\:{Parkash} \\ $$$${THANKS}\:{for}\:{guidance}.{I}\:{was}\:{wrong}.\:{I}\:{did}\:{not}\:{understand} \\ $$$${the}\:{logic}\:{of}\:{Mr}\:\mathrm{123456}\:{at}\:{first}!\:{But}\:{now}\:{I}\:{do}\:\left({with}\:{your}\:{help}\right). \\ $$$${Appreciation}\:{for}\:\:\mathrm{123456} \\ $$
