Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 114739 by mr W last updated on 20/Sep/20

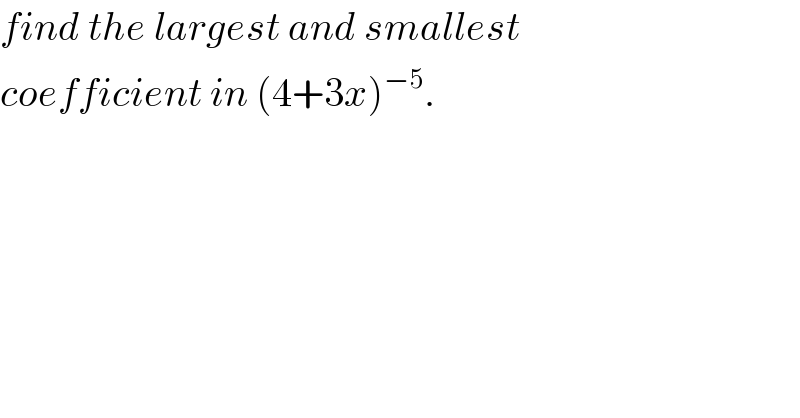
find the largest and smallest coefficient in (4+3x)^(−5) .

$${find}\:{the}\:{largest}\:{and}\:{smallest} \\ $$$${coefficient}\:{in}\:\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} . \\ $$

Answered by mr W last updated on 20/Sep/20

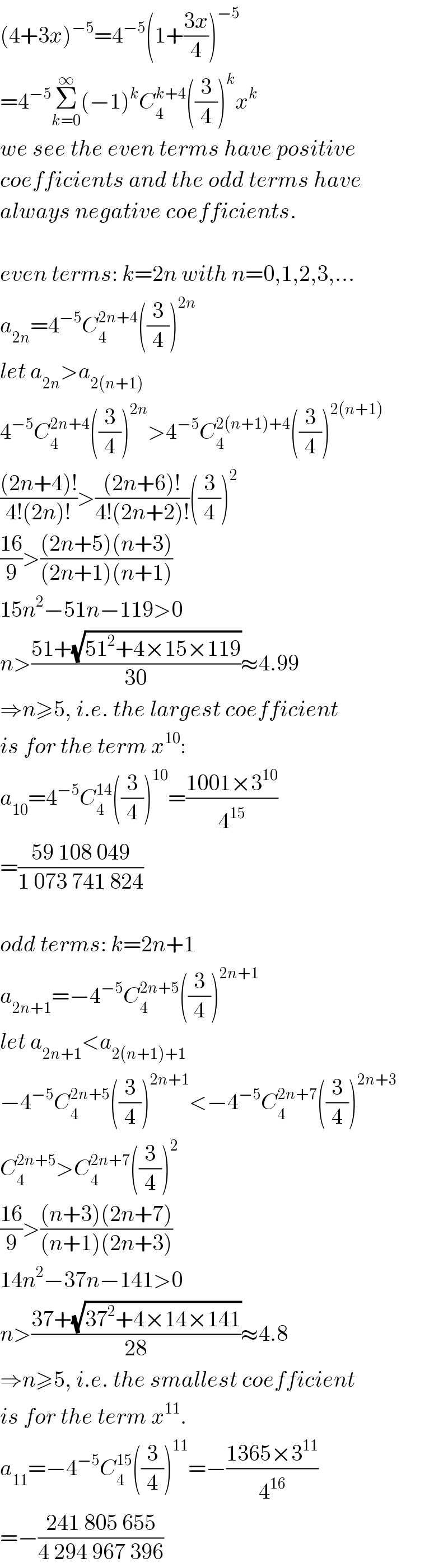
(4+3x)^(−5) =4^(−5) (1+((3x)/4))^(−5) =4^(−5) Σ_(k=0) ^∞ (−1)^k C_4 ^(k+4) ((3/4))^k x^k we see the even terms have positive coefficients and the odd terms have always negative coefficients. even terms: k=2n with n=0,1,2,3,... a_(2n) =4^(−5) C_4 ^(2n+4) ((3/4))^(2n) let a_(2n) >a_(2(n+1)) 4^(−5) C_4 ^(2n+4) ((3/4))^(2n) >4^(−5) C_4 ^(2(n+1)+4) ((3/4))^(2(n+1)) (((2n+4)!)/(4!(2n)!))>(((2n+6)!)/(4!(2n+2)!))((3/4))^2 ((16)/9)>(((2n+5)(n+3))/((2n+1)(n+1))) 15n^2 −51n−119>0 n>((51+(√(51^2 +4×15×119)))/(30))≈4.99 ⇒n≥5, i.e. the largest coefficient is for the term x^(10) : a_(10) =4^(−5) C_4 ^(14) ((3/4))^(10) =((1001×3^(10) )/4^(15) ) =((59 108 049)/(1 073 741 824)) odd terms: k=2n+1 a_(2n+1) =−4^(−5) C_4 ^(2n+5) ((3/4))^(2n+1) let a_(2n+1) <a_(2(n+1)+1) −4^(−5) C_4 ^(2n+5) ((3/4))^(2n+1) <−4^(−5) C_4 ^(2n+7) ((3/4))^(2n+3) C_4 ^(2n+5) >C_4 ^(2n+7) ((3/4))^2 ((16)/9)>(((n+3)(2n+7))/((n+1)(2n+3))) 14n^2 −37n−141>0 n>((37+(√(37^2 +4×14×141)))/(28))≈4.8 ⇒n≥5, i.e. the smallest coefficient is for the term x^(11) . a_(11) =−4^(−5) C_4 ^(15) ((3/4))^(11) =−((1365×3^(11) )/4^(16) ) =−((241 805 655)/(4 294 967 396))

$$\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} =\mathrm{4}^{−\mathrm{5}} \left(\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{−\mathrm{5}} \\ $$$$=\mathrm{4}^{−\mathrm{5}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{\mathrm{4}} ^{{k}+\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{k}} {x}^{{k}} \\ $$$${we}\:{see}\:{the}\:{even}\:{terms}\:{have}\:{positive} \\ $$$${coefficients}\:{and}\:{the}\:{odd}\:{terms}\:{have} \\ $$$${always}\:{negative}\:{coefficients}. \\ $$$$ \\ $$$${even}\:{terms}:\:{k}=\mathrm{2}{n}\:{with}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},... \\ $$$${a}_{\mathrm{2}{n}} =\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}{n}} \\ $$$${let}\:{a}_{\mathrm{2}{n}} >{a}_{\mathrm{2}\left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}{n}} >\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}\left({n}+\mathrm{1}\right)+\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}\left({n}+\mathrm{1}\right)} \\ $$$$\frac{\left(\mathrm{2}{n}+\mathrm{4}\right)!}{\mathrm{4}!\left(\mathrm{2}{n}\right)!}>\frac{\left(\mathrm{2}{n}+\mathrm{6}\right)!}{\mathrm{4}!\left(\mathrm{2}{n}+\mathrm{2}\right)!}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{16}}{\mathrm{9}}>\frac{\left(\mathrm{2}{n}+\mathrm{5}\right)\left({n}+\mathrm{3}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{15}{n}^{\mathrm{2}} −\mathrm{51}{n}−\mathrm{119}>\mathrm{0} \\ $$$${n}>\frac{\mathrm{51}+\sqrt{\mathrm{51}^{\mathrm{2}} +\mathrm{4}×\mathrm{15}×\mathrm{119}}}{\mathrm{30}}\approx\mathrm{4}.\mathrm{99} \\ $$$$\Rightarrow{n}\geqslant\mathrm{5},\:{i}.{e}.\:{the}\:{largest}\:{coefficient} \\ $$$${is}\:{for}\:{the}\:{term}\:{x}^{\mathrm{10}} : \\ $$$${a}_{\mathrm{10}} =\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{14}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{10}} =\frac{\mathrm{1001}×\mathrm{3}^{\mathrm{10}} }{\mathrm{4}^{\mathrm{15}} } \\ $$$$=\frac{\mathrm{59}\:\mathrm{108}\:\mathrm{049}}{\mathrm{1}\:\mathrm{073}\:\mathrm{741}\:\mathrm{824}} \\ $$$$ \\ $$$${odd}\:{terms}:\:{k}=\mathrm{2}{n}+\mathrm{1} \\ $$$${a}_{\mathrm{2}{n}+\mathrm{1}} =−\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{5}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${let}\:{a}_{\mathrm{2}{n}+\mathrm{1}} <{a}_{\mathrm{2}\left({n}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$−\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{5}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}{n}+\mathrm{1}} <−\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{7}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}{n}+\mathrm{3}} \\ $$$${C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{5}} >{C}_{\mathrm{4}} ^{\mathrm{2}{n}+\mathrm{7}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{16}}{\mathrm{9}}>\frac{\left({n}+\mathrm{3}\right)\left(\mathrm{2}{n}+\mathrm{7}\right)}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$$\mathrm{14}{n}^{\mathrm{2}} −\mathrm{37}{n}−\mathrm{141}>\mathrm{0} \\ $$$${n}>\frac{\mathrm{37}+\sqrt{\mathrm{37}^{\mathrm{2}} +\mathrm{4}×\mathrm{14}×\mathrm{141}}}{\mathrm{28}}\approx\mathrm{4}.\mathrm{8} \\ $$$$\Rightarrow{n}\geqslant\mathrm{5},\:{i}.{e}.\:{the}\:{smallest}\:{coefficient} \\ $$$${is}\:{for}\:{the}\:{term}\:{x}^{\mathrm{11}} . \\ $$$${a}_{\mathrm{11}} =−\mathrm{4}^{−\mathrm{5}} {C}_{\mathrm{4}} ^{\mathrm{15}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{11}} =−\frac{\mathrm{1365}×\mathrm{3}^{\mathrm{11}} }{\mathrm{4}^{\mathrm{16}} } \\ $$$$=−\frac{\mathrm{241}\:\mathrm{805}\:\mathrm{655}}{\mathrm{4}\:\mathrm{294}\:\mathrm{967}\:\mathrm{396}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com