Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114768 by ZiYangLee last updated on 21/Sep/20

Solve for ∣x−2∣+∣1−x∣=4

$$\mathrm{Solve}\:\mathrm{for}\:\mid{x}−\mathrm{2}\mid+\mid\mathrm{1}−{x}\mid=\mathrm{4} \\ $$

Answered by bobhans last updated on 21/Sep/20

(1) x<1 ⇒ 2−x+1−x=4 3−2x = 4 ; x=−(1/2) (2) 1≤x<2⇒2−x+x−1=4 1=4 ←no solution (3)x≥2 ⇒x−2+x−1=4 2x = 7; x=(7/2) ∴ x = −(1/2) or x = (7/2)

$$\left(\mathrm{1}\right)\:{x}<\mathrm{1}\:\Rightarrow\:\mathrm{2}−{x}+\mathrm{1}−{x}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−\mathrm{2}{x}\:=\:\mathrm{4}\:;\:{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{1}\leqslant{x}<\mathrm{2}\Rightarrow\mathrm{2}−{x}+{x}−\mathrm{1}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}=\mathrm{4}\:\leftarrow{no}\:{solution} \\ $$$$\left(\mathrm{3}\right){x}\geqslant\mathrm{2}\:\Rightarrow{x}−\mathrm{2}+{x}−\mathrm{1}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}\:=\:\mathrm{7};\:{x}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\therefore\:{x}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:{x}\:=\:\frac{\mathrm{7}}{\mathrm{2}} \\ $$

Answered by mathmax by abdo last updated on 22/Sep/20

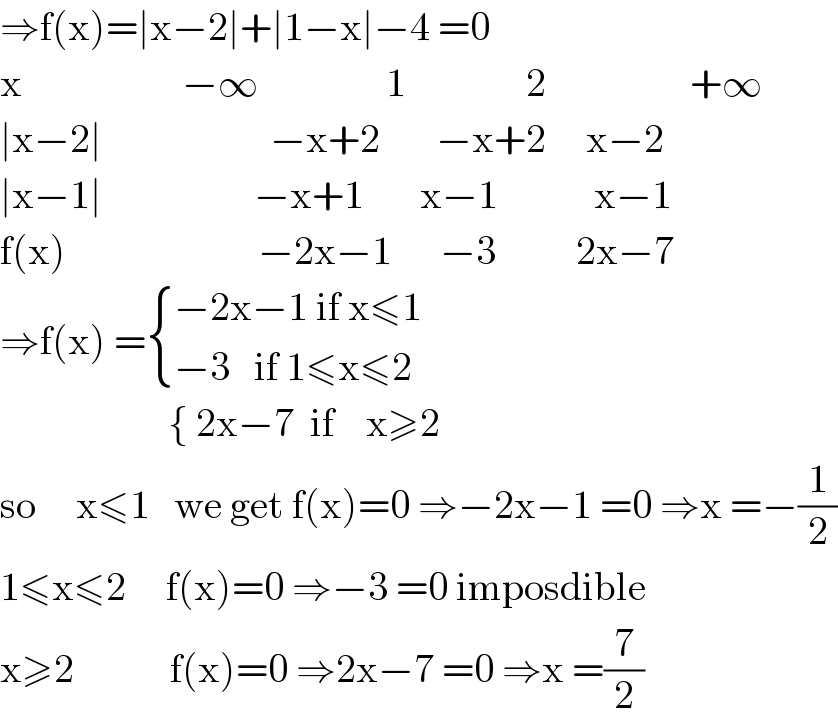
⇒f(x)=∣x−2∣+∣1−x∣−4 =0 x −∞ 1 2 +∞ ∣x−2∣ −x+2 −x+2 x−2 ∣x−1∣ −x+1 x−1 x−1 f(x) −2x−1 −3 2x−7 ⇒f(x) = { ((−2x−1 if x≤1)),((−3 if 1≤x≤2 )) :} { 2x−7 if x≥2 so x≤1 we get f(x)=0 ⇒−2x−1 =0 ⇒x =−(1/2) 1≤x≤2 f(x)=0 ⇒−3 =0 imposdible x≥2 f(x)=0 ⇒2x−7 =0 ⇒x =(7/2)

$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mid\mathrm{x}−\mathrm{2}\mid+\mid\mathrm{1}−\mathrm{x}\mid−\mathrm{4}\:=\mathrm{0}\:\: \\ $$$$\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid\mathrm{x}−\mathrm{2}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}+\mathrm{2}\:\:\:\:\:\:\:−\mathrm{x}+\mathrm{2}\:\:\:\:\:\mathrm{x}−\mathrm{2} \\ $$$$\mid\mathrm{x}−\mathrm{1}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}+\mathrm{1}\:\:\:\:\:\:\:\mathrm{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2x}−\mathrm{1}\:\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{2x}−\mathrm{7} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\begin{cases}{−\mathrm{2x}−\mathrm{1}\:\mathrm{if}\:\mathrm{x}\leqslant\mathrm{1}}\\{−\mathrm{3}\:\:\:\mathrm{if}\:\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{2}\:\:\:\:\:}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\:\mathrm{2x}−\mathrm{7}\:\:\mathrm{if}\:\:\:\:\mathrm{x}\geqslant\mathrm{2}\right. \\ $$$$\mathrm{so}\:\:\:\:\:\mathrm{x}\leqslant\mathrm{1}\:\:\:\mathrm{we}\:\mathrm{get}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow−\mathrm{2x}−\mathrm{1}\:=\mathrm{0}\:\Rightarrow\mathrm{x}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{2}\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow−\mathrm{3}\:=\mathrm{0}\:\mathrm{imposdible} \\ $$$$\mathrm{x}\geqslant\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{2x}−\mathrm{7}\:=\mathrm{0}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{7}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com