Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 11477 by @ANTARES_VY last updated on 26/Mar/17

((a^8 +a^4 +1)/(a^6 +1)). solves....

$$\frac{\boldsymbol{\mathrm{a}}^{\mathrm{8}} +\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\mathrm{1}}{\boldsymbol{\mathrm{a}}^{\mathrm{6}} +\mathrm{1}}. \\ $$$$\boldsymbol{\mathrm{solves}}.... \\ $$

Answered by sm3l2996 last updated on 26/Mar/17

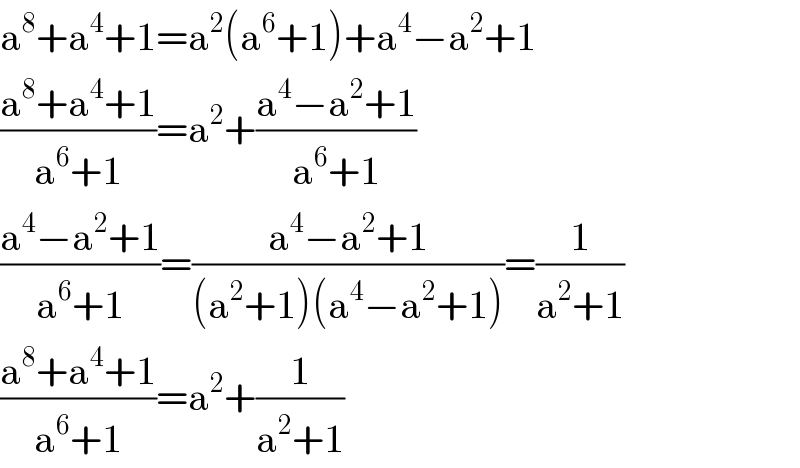
a^8 +a^4 +1=a^2 (a^6 +1)+a^4 −a^2 +1 ((a^8 +a^4 +1)/(a^6 +1))=a^2 +((a^4 −a^2 +1)/(a^6 +1)) ((a^4 −a^2 +1)/(a^6 +1))=((a^4 −a^2 +1)/((a^2 +1)(a^4 −a^2 +1)))=(1/(a^2 +1)) ((a^8 +a^4 +1)/(a^6 +1))=a^2 +(1/(a^2 +1))

$$\mathrm{a}^{\mathrm{8}} +\mathrm{a}^{\mathrm{4}} +\mathrm{1}=\mathrm{a}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{6}} +\mathrm{1}\right)+\mathrm{a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1} \\ $$$$\frac{\mathrm{a}^{\mathrm{8}} +\mathrm{a}^{\mathrm{4}} +\mathrm{1}}{\mathrm{a}^{\mathrm{6}} +\mathrm{1}}=\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{a}^{\mathrm{6}} +\mathrm{1}} \\ $$$$\frac{\mathrm{a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{a}^{\mathrm{6}} +\mathrm{1}}=\frac{\mathrm{a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{a}^{\mathrm{8}} +\mathrm{a}^{\mathrm{4}} +\mathrm{1}}{\mathrm{a}^{\mathrm{6}} +\mathrm{1}}=\mathrm{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

Thenks.

$$\boldsymbol{\mathrm{T}}\mathrm{henks}. \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

Thenks.

$$\boldsymbol{\mathrm{T}}\mathrm{henks}. \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

Thenks.

$$\boldsymbol{\mathrm{T}}\mathrm{henks}. \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

Thenks.

$$\boldsymbol{\mathrm{T}}\mathrm{henks}. \\ $$

Commented by sma3l2996 last updated on 27/Mar/17

you welcome

$${you}\:{welcome} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

a^2 =p⇒((p^4 +p^2 +1)/(p^3 +1))=(((p^6 −1)/(p^2 −1))/(p^3 +1))=(((p^3 +1)(p^3 −1))/((p^3 +1)(p^2 −1))) =(((p−1)(p^2 +p+1))/((p−1)(p+1)))=((p^2 +p+1)/(p+1))=((a^4 +a^2 +1)/(a^2 +1)) (((a^2 +1)^2 −a^2 )/(a^2 +1))=(((a^2 +a+1)(a^2 −a+1))/(a^2 +1))

$${a}^{\mathrm{2}} ={p}\Rightarrow\frac{{p}^{\mathrm{4}} +{p}^{\mathrm{2}} +\mathrm{1}}{{p}^{\mathrm{3}} +\mathrm{1}}=\frac{\frac{{p}^{\mathrm{6}} −\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{1}}}{{p}^{\mathrm{3}} +\mathrm{1}}=\frac{\left({p}^{\mathrm{3}} +\mathrm{1}\right)\left({p}^{\mathrm{3}} −\mathrm{1}\right)}{\left({p}^{\mathrm{3}} +\mathrm{1}\right)\left({p}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\frac{\left({p}−\mathrm{1}\right)\left({p}^{\mathrm{2}} +{p}+\mathrm{1}\right)}{\left({p}−\mathrm{1}\right)\left({p}+\mathrm{1}\right)}=\frac{{p}^{\mathrm{2}} +{p}+\mathrm{1}}{{p}+\mathrm{1}}=\frac{{a}^{\mathrm{4}} +{a}^{\mathrm{2}} +\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{1}}=\frac{\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com