Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114790 by manuel2456 last updated on 21/Sep/20

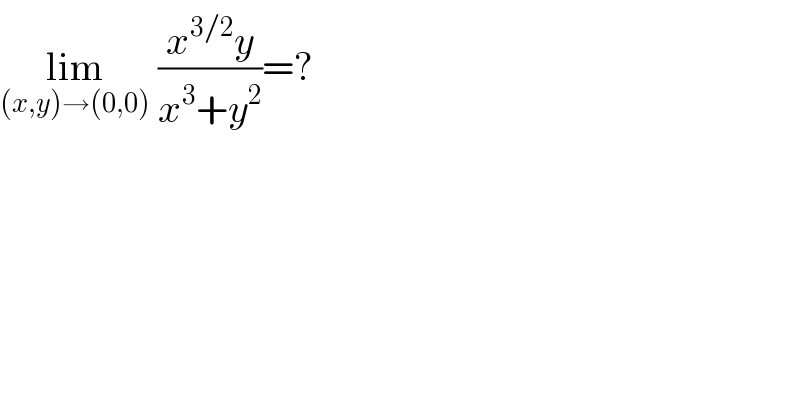
lim_((x,y)→(0,0)) ((x^(3/2) y)/(x^3 +y^2 ))=?

$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}/\mathrm{2}} {y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} }=? \\ $$

Answered by Olaf last updated on 26/Sep/20

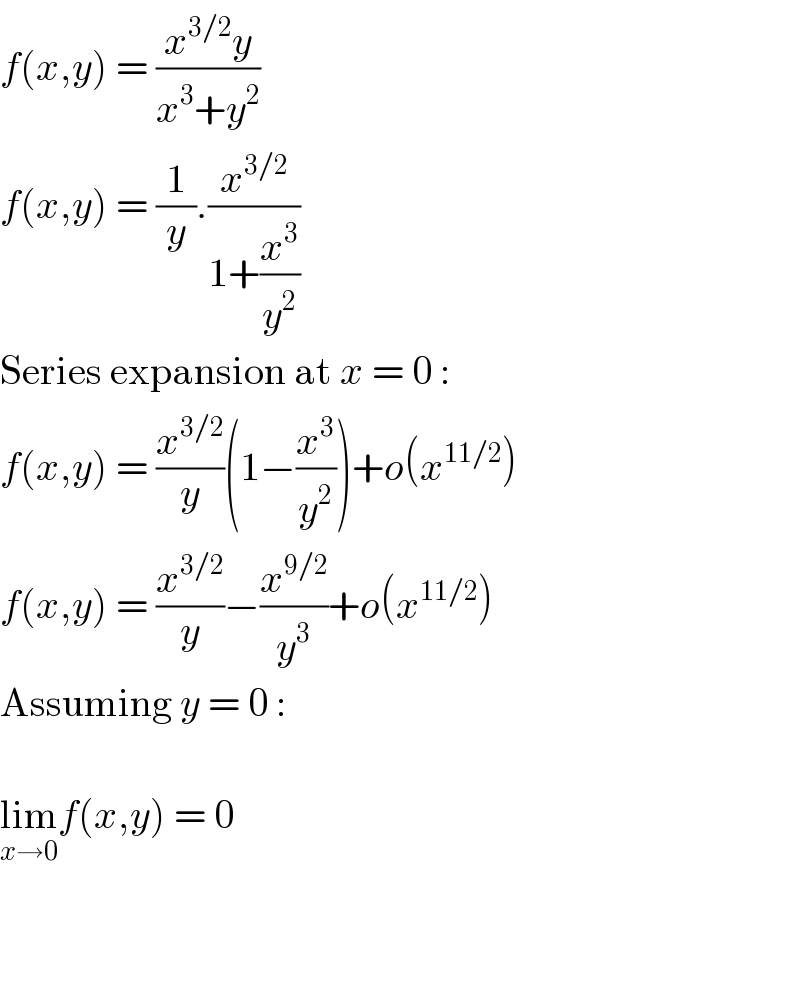
f(x,y) = ((x^(3/2) y)/(x^3 +y^2 )) f(x,y) = (1/y).(x^(3/2) /(1+(x^3 /y^2 ))) Series expansion at x = 0 : f(x,y) = (x^(3/2) /y)(1−(x^3 /y^2 ))+o(x^(11/2) ) f(x,y) = (x^(3/2) /y)−(x^(9/2) /y^3 )+o(x^(11/2) ) Assuming y = 0 : lim_(x→0) f(x,y) = 0

$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} {y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} } \\ $$$${f}\left({x},{y}\right)\:=\:\frac{\mathrm{1}}{{y}}.\frac{{x}^{\mathrm{3}/\mathrm{2}} }{\mathrm{1}+\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{2}} }} \\ $$$$\mathrm{Series}\:\mathrm{expansion}\:\mathrm{at}\:{x}\:=\:\mathrm{0}\:: \\ $$$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} }{{y}}\left(\mathrm{1}−\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{2}} }\right)+{o}\left({x}^{\mathrm{11}/\mathrm{2}} \right) \\ $$$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} }{{y}}−\frac{{x}^{\mathrm{9}/\mathrm{2}} }{{y}^{\mathrm{3}} }+{o}\left({x}^{\mathrm{11}/\mathrm{2}} \right) \\ $$$$\mathrm{Assuming}\:{y}\:=\:\mathrm{0}\:: \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x},{y}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com