Question Number 114807 by Eric002 last updated on 21/Sep/20

is zero a natural number 0∈N?

Commented byMJS_new last updated on 21/Sep/20

there seem to be two different definitions of N, both are in use... confusion... old definition N={1, 2, 3, ...}; N∪{0}=N_0 new definition N={0, 1, 2, ...}; N\{0}=N^★ so the answer depends on in which country and on which school you are when I was in school (a zillion years ago) we leaned these things one after the other: (1) N: as you count (nobody would start to count by 0). (1.1) addition is always possible in N (1.2) multiplication is always possible in N but n×1=n (1.3) substraction only as a test of addition a+b=c ⇒ c−b=a∧c−a=b (1.4) substraction a−b possible only if a>b? ⇒ (2) Z=N∪{...−2, −1, 0} these are magical numbers we need to substract without limits a−b=x always solveable in Z (2.1) 0 neutral element of addition (2.2) 1 neutral element of multiplication then Q (a÷b=x solveable), then R (all non− periodic numbers like (√2), π; later e...), finally C

Commented byEric002 last updated on 21/Sep/20

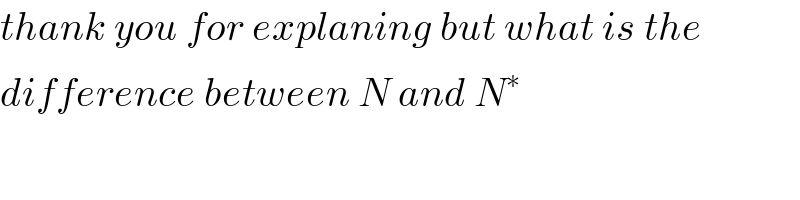
thank you for explaning but what is the difference between N and N^∗

Commented byMJS_new last updated on 21/Sep/20

the old N is the same as the new N^★ ={1, 2, 3, ...} the old N_0 is the same as the new N ={0, 1, 2, ...}

Commented byEric002 last updated on 21/Sep/20

thank you sir

Commented byRasheed.Sindhi last updated on 21/Sep/20

Why isn′t there any international institute which play roll in this connection? Which make standards so that such confusions be killed?

Commented byMJS_new last updated on 21/Sep/20

standards are no longer accepted in the age of internet; everybody′s own opinion counts more than any standard

Commented byRasheed.Sindhi last updated on 21/Sep/20

ThankSs Sir!