Question Number 114857 by Rio Michael last updated on 21/Sep/20

we know that e^(πi) = −1 ⇒ ln (e^(πi) ) = ln(−1) πi = ln (−1). How good is this prove?

Commented bymalwan last updated on 21/Sep/20

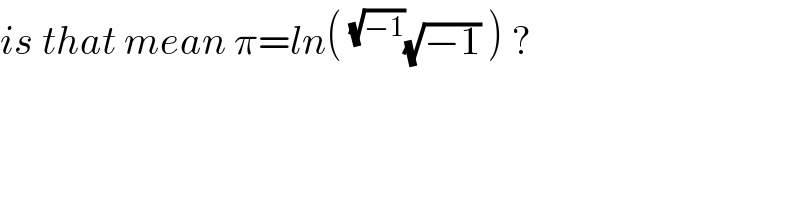
is that mean π=ln( ^(√(−1)) (√(−1)) ) ?

Commented bymr W last updated on 21/Sep/20

you can even say π=ln ((−1))^(1/i)

Commented byRio Michael last updated on 21/Sep/20

really sir?

Commented byMJS_new last updated on 21/Sep/20

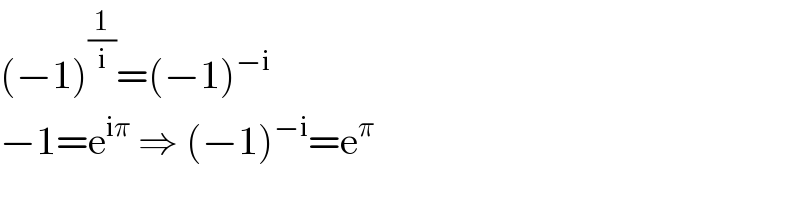
(−1)^(1/i) =(−1)^(−i) −1=e^(iπ) ⇒ (−1)^(−i) =e^π

Commented byRio Michael last updated on 21/Sep/20

thanks prof

Commented byDwaipayan Shikari last updated on 21/Sep/20

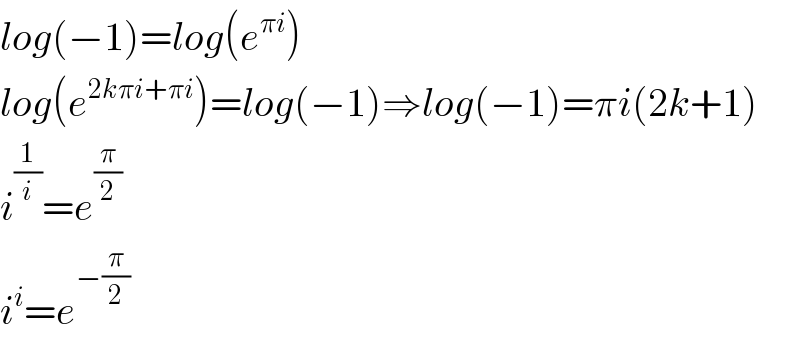
log(−1)=log(e^(πi) ) log(e^(2kπi+πi) )=log(−1)⇒log(−1)=πi(2k+1) i^(1/i) =e^(π/2) i^i =e^(−(π/2))

Commented byMJS_new last updated on 21/Sep/20

yes